干货 | 数据结构之图论基础

前言

一个好的程序=算法+数据结构

数据结构是程序的核心之一，可惜本公众内关于数据结构的文章略显不足，于是何小编打算与向柯玮小编一起把数据结构这部分补齐，来满足各位观众大老爷。

图的储存

邻接矩阵

首先我们先来介绍一下图的基本存储方式，同时也是最简单容易的图（ADT）的实现方式。本质使用二维数列A[n][n]表示由n个顶点构成的图，其中每个单元，各自负责描述一对顶点之间可能存在的邻接关系，故此得名。

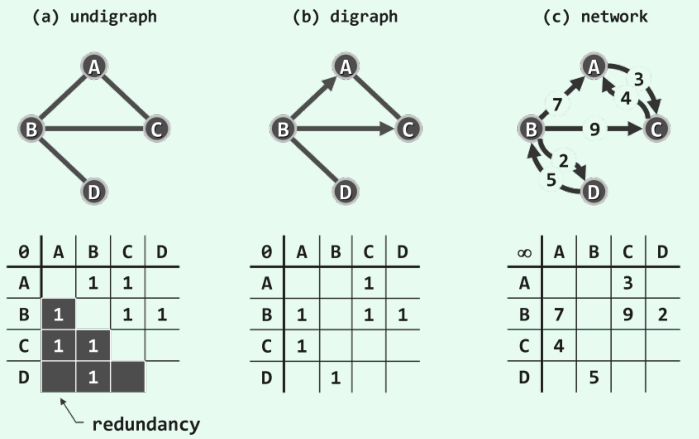
若图为无权图，则A[i][j]联通的情况下赋值为1。下图中的a和b分别为无向图和有向图的邻接矩阵的样例，对于不存在的边可以赋值为无穷或0。

下为其C++代码

#define MAXNum 4/*邻接矩阵存储表示*//*MAXNum为定义的最多点数以下都为此义*/typedef struct GraphMatrix{    int isDiGraph;    char vexs[MAXNum];            //顶点表    int arcs[MAXNum][MAXNum];      //邻接矩阵    int vexnum, arcnum;          //当前的顶点数和边数};/*找到顶点v的对应下标*/int LocateVex(GraphMatrix& G, char v){    int i;    for (i = 0; i < G.vexnum; i++)        if (G.vexs[i] == v)            return i;}/*采用邻接矩阵表示法，创建无向图G*/void Create(GraphMatrix& G){    int i, j, k, w;    char v1, v2;    cin >> G.isDiGraph >> G.vexnum >> G.arcnum;              //输入总顶点数，总边数    for (i = 0; i < G.vexnum; i++)        cin >> G.vexs[i];      //依次输入点的信息    for (i = 0; i < G.vexnum; i++)        for (j = 0; j < G.vexnum; j++)            G.arcs[i][j] = 0;      //初始化邻接矩阵边，0表示顶点i和j之间无边    for (k = 0; k < G.arcnum; k++)    {        cin >> v1 >> v2>> w;      //输入一条边依附的顶点        i = LocateVex(G, v1);        //找到顶点i的下标        j = LocateVex(G, v2);        //找到顶点j的下标        G.arcs[i][j] = w;        if(!G.isDiGraph)G.arcs[i][j] = G.arcs[j][i] = 1;          //1表示顶点i和j之间有边，无向图不区分方向    }}

性能分析

时间和空间性能分析

时间性能：

依据上面的代码分析，当进行静态操作时由于向量“循秩访问”的特长与优势，操作均需O(1)时间。然而在顶点的动态操作上面却很耗时。为了插入新的顶点，顶点集向量V[]需要添加一个元素；边集向量E[][]也需要增加一行，且每行都需要添加一个元素，删除也是一样，单次操作的耗时为O(n)。这也是这种向量结构的不足。

空间性能：

上述实现方式所用空间，主要消耗于邻接矩阵，即其中的二维边集向量E[][]。由于Vector结构的装填因子始终不低于50%，故空间总量渐进地不超过O(n  n) = O(n^2)。

当然对于无相图，无向图的邻接矩阵必为对称矩阵。每条边都被储存了两篇，接近一半的空间被浪费了，因此可以通过压缩储存的方法来提高空间性能。

图的实现的进一步优化

邻接表

就其有向图的实现，其O(n^2)的空间还有极大的优化余地，此方法虽然可以存储所有的边，但是对于稀疏图来说，很多单元对应的边事实上并未体现。邻接表就是解决这个问题的一种方法.

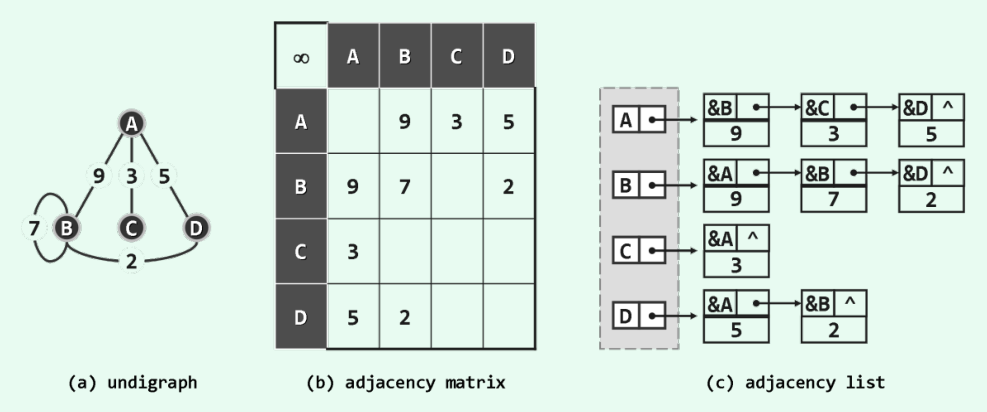
以上图中的无向图为例，只需要将b图依次转化为c图中的邻接表。省略掉不存在的边，可以大大优化稀疏表的空间性能。

下附代码实现

#define MAXNum 4/*邻接表存储表示*/typedef struct EdgeNode          //边结点{    int adjvex;    //该边所指向的顶点的位置    EdgeNode* next;  //指向下一条边的指针    int weight;    //和边相关的信息，如权值}edgeNode;
typedef struct HeadNode    //表头结点{    char data;    EdgeNode* firstarc;  //指向第一条依附该顶点的边的指针}headNode, AdjList[MAXNum]; //AbjList表示一个表头结点表
typedef struct ALGraph{    AdjList vertices;    int vexnum, arcnum;}ALGraph;

int LocateVex(ALGraph& G, char v)/*找到顶点v的对应下标*/{    int i;    for (i = 0; i < G.vexnum; i++)        if (G.vertices[i].data == v)            return i;}
void Create(ALGraph& G){    int i, j, k, w;    char v1, v2;    cin >> G.vexnum >> G.arcnum;          //输入总顶点数，总边数    for (i = 0; i < G.vexnum; i++)      //输入各顶点，构造表头结点表    {        cin >> G.vertices[i].data;  //输入顶点值        G.vertices[i].firstarc = NULL;    //初始化每个表头结点的指针域为NULL    }    for (k = 0; k < G.arcnum; k++)      //输入各边，构造邻接表    {        cin >> v1 >> v2 >> w;      //输入一条边依附的两个顶点        i = LocateVex(G, v1);        //找到顶点i的下标        j = LocateVex(G, v2);        //找到顶点j的下标        EdgeNode* p1 = new EdgeNode;      //创建一个边结点*p1        p1->adjvex = j;            //其邻接点域为j        p1->next = G.vertices[i].firstarc;        p1->weight = w;        G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部        /*若为无向图*/     /* EdgeNode* p2 = new EdgeNode;      //生成另一个对称的新的表结点*p2        p2->adjvex = i;        p2->next = G.vertices[j].firstarc;        G.vertices[j].firstarc = p2;*/    }}

复杂度分析

        可见，邻接表所含列表数等于顶点总数n，每条边在其中仅存放一次（有向图）或两次（无向图），故空间总量为O(n + e)，与图自身的规模相当，较之邻接矩阵有很大改进。

        当然，空间性能的这一改进，需以某些方面时间性能的降低为代价。例如查询两点之间是否存在边时共需O(n)时间。

同时，在顶点的处理上，插入顶点的时间复杂度变为了O(1)，美中不足的是，其删除顶点的时间复杂度还是O(n)。

与邻接矩阵相比，邻接表在单个边的处理上略显乏力，但是它在批量处理上有着强大的优势，因此总体上我们还是偏向于邻接表。

图的遍历

广度优先搜索(BFS)

图的各种搜索之间所得的遍历树不同的决定性因素在于搜索中每一步之后将按照何种策略来选取下一步，这就是BFS和DFS的差别所在。接下来就来了解一下。

广度优先搜索

在遍历的过程中，我们相当于图转化为一个树，每个节点假设都有一个固定的深度，BFS的操作就是每次遍历的时候都先将同一深度的节点遍历完后再进行下一层的遍历。而下一层的节点我们预先是不知道的，是需要由上一层节点的边来确定，那么我们就需要一个队列将上一层节点保存下来，此时队列中的节点的深度为k，将深度为k的节点扩展后的节点深度为k+1，将这些点中之前未被访问过的插入到队列后方，保证了先将k层的遍历完后，再进行k+1层的遍历。同时也要将已经进行扩展的节点移除队列，避免重复访问。

由于每一次迭代都有一个节点被访问，因此至多迭代n次，另一方面，因为不会遗漏每个刚被访问顶点的任何邻居，故对于无向图必能覆盖s所属的连通分量（connected component），对于有向图必能覆盖以s为起点的可达分量（reachable component）。倘若还有来自其它连通分量或可达分量的顶点，则不妨从该顶点出发，重复上述过程。

        时间方面，首先需花费O(n + e)时间复位所有顶点和边的状态。不计对子函数BFS()的调用，bfs()本身对所有顶点的枚举共需O(n)时间。而在对BFS()的所有调用中，每个顶点、每条边均只耗费O(1)时间，累计O(n + e)。综合起来，BFS搜索总体仅需O(n + e)时间。

        下图是以S为起始节点开始的BFS示例

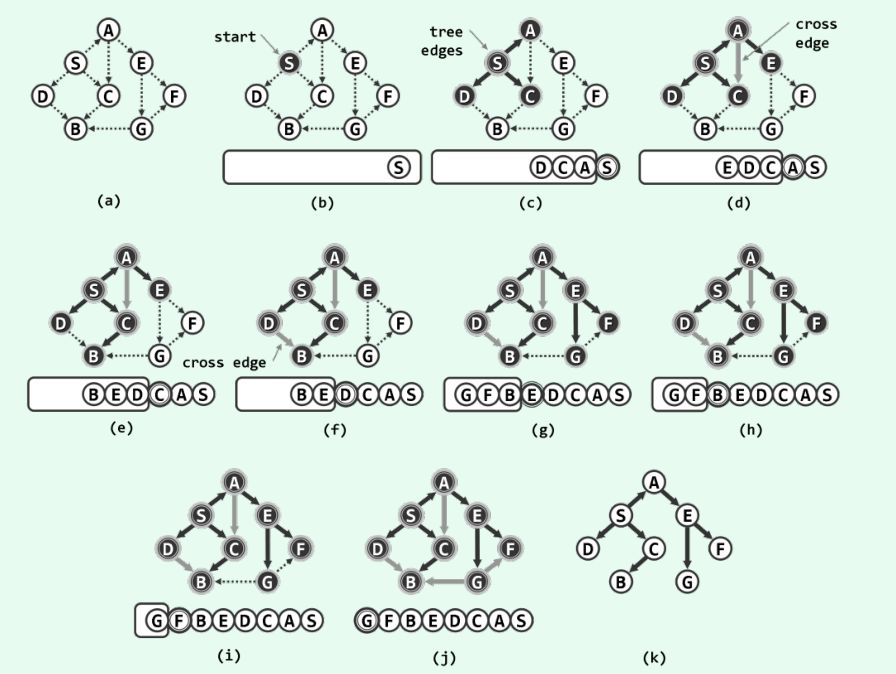
下为代码实现

/*采用邻接表表示图的广度优先遍历*/void BFS(ALGraph &G, char v0){  int u,w,v;  EdgeNode *p;  cin>> v0;                                            //打印顶点v0  v = LocateVex(G, v0);                                                  //找到v0对应的下标  visited[v] = 1;                                              //顶点v0已被访问  q.push(v0);                                        //将顶点v0入队  while (!q.empty())  {    u = q.front();                                            //将顶点元素u出队，开始访问u的所有邻接点    v = LocateVex(G, u);                                            //得到顶点u的对应下标    q.pop();      //将顶点u出队    for (p = G.vertices[v].firstarc; p; p = p->nextarc)    //遍历顶点u的邻接点    {      w = p->adjvex;        if (!visited[w])  //顶点p未被访问      {        printf("%c ", G.vertices[w].data);          //打印顶点p        visited[w] = 1;                //顶点p已被访问        q.push(G.vertices[w].data);      //将顶点p入队      }    }  }}

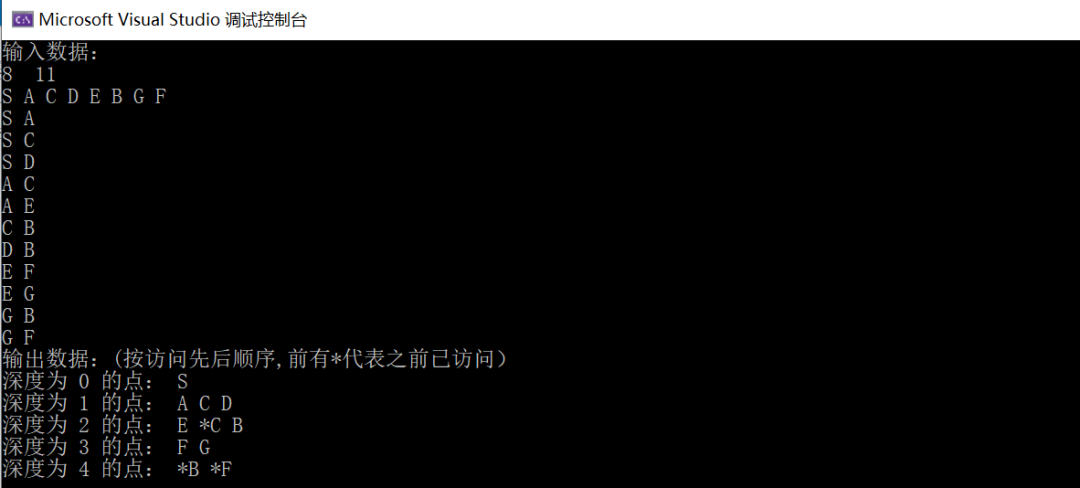
图的搜索

深度优先搜索(DFS)

与BFS不同，DFS是一条路走到黑的（原谅本小编太菜了，说不明白）由递归完成。

   每一次递归，都先将当前节点v标记为DISCOVERED（已发现）状态，再逐一核对其各邻居u的状态并做相应处理。待其所有邻居均已处理完毕之后，将顶点v置为VISITED（访问完毕）状态，便可回溯。

        若节点u为UNDISCOVERED（未发现）状态，则将边(v, u)为遍历树上的一条边。若节点u为DISCOVERED（发现）状态。

        若顶点u处于DISCOVERED状态，则意味着在此处发现一个有向环路。此时，在DFS遍历树中u必为v的祖先。对于有向图，顶点u还可能处于VISITED状态。此时，只要比对v与u的活跃期，即可判定在DFS树中v是否为u的祖先。

        这里为每个顶点v都记录了被发现的和访问完成的时刻。至于为什么要用两个记录，这是为了判断在有向图中是否为强连通量的问题，这里我们先不解释，大家有兴趣可以查阅一下资料。

        在回溯返回后，所有的VISITED的点可以确定了父子关系，形成了一棵遍历树。这就是我们需要的DFS树，与BFS搜索一样，此时若还有其它的连通或可达分量，则可以其中任何顶点为基点，再次启动DFS搜索。

        接下来就是时间分析了。每次迭代中对所有顶点的枚举共需O(n)时间。每个顶点、每条边只在子函数DFS()的某一递归实例中耗费O(1)时间，故累计亦不过O(n + e)时间。（忽略了函数的调用用的时间）综合而言，深度优先搜索算法也可在O(n + e)时间内完成。

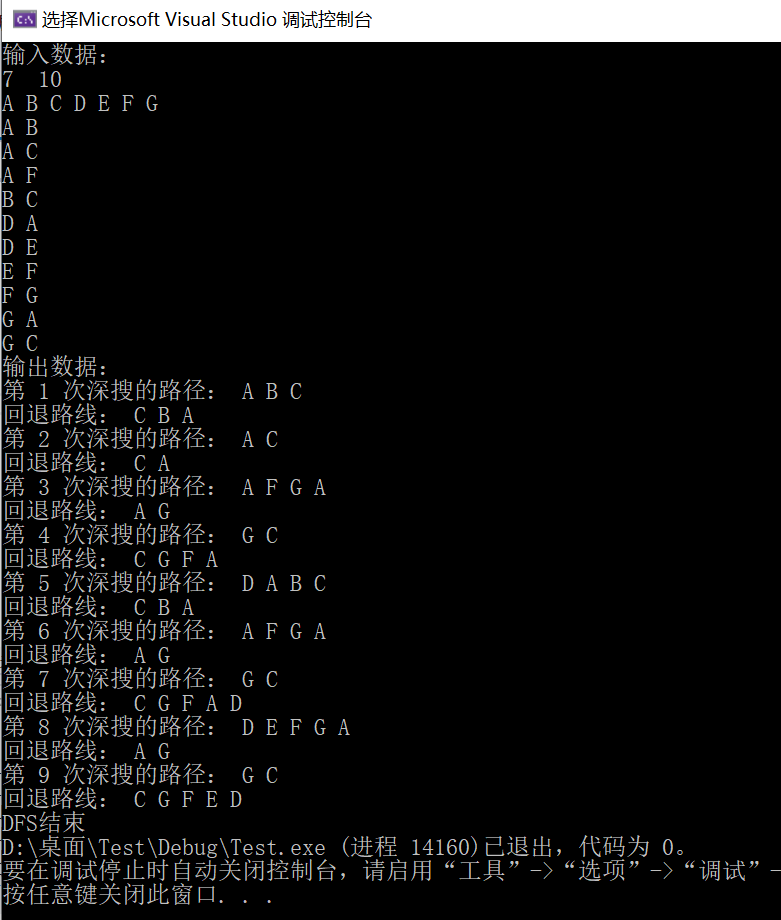
        下为一个7点，10边的有向图进行DFS的详细过程，大家可以研究下。

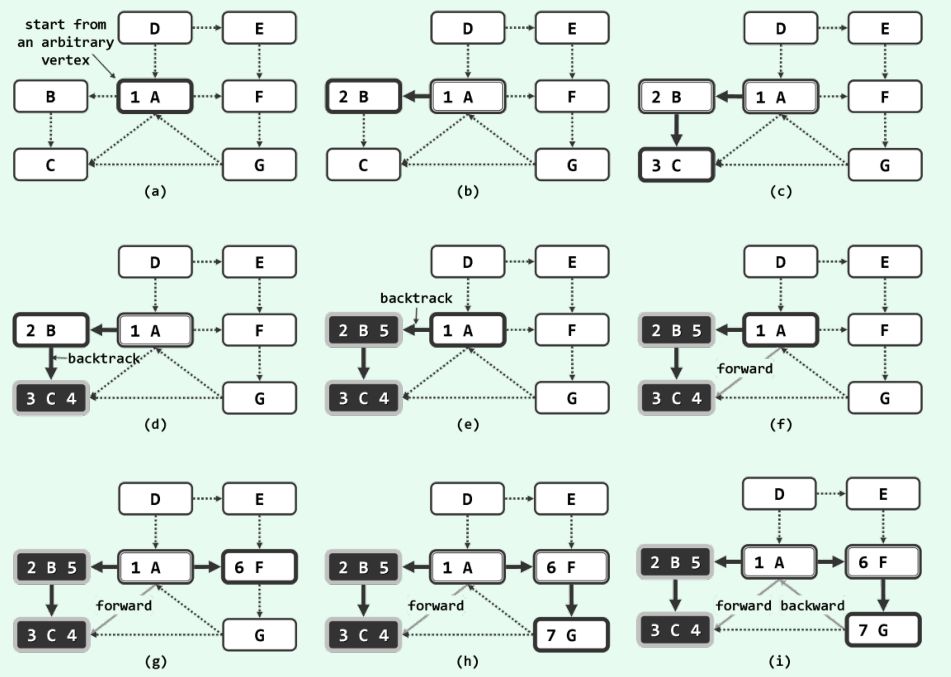
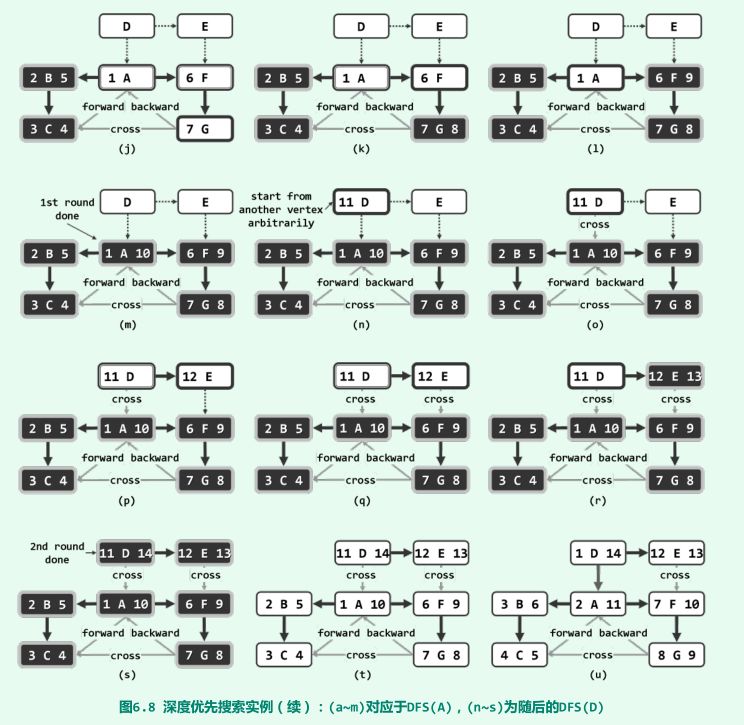
（粗边框白色，为当前顶点；细边框白色、双边框白色和黑色，分别为处于UNDISCOVERED、DISCOVERED和VISITED状态的顶点，左上角的数字为被发现时的序号，右上角的数字为访问完成时的数据）

下为代码实现

void DFS(ALGraph &G, int v){  int w;  cin>>G.vertices[v].data;  visited[v] = 1;  EdgeNode *p = new EdgeNode;  p = G.vertices[v].firstarc;  while (p)  {    w = p->adjvex;    if (!visited[w]) DFS_AL(G, w);    p = p->nextarc;  }}