三角测量原理与双目视觉景深恢复
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
1.引言
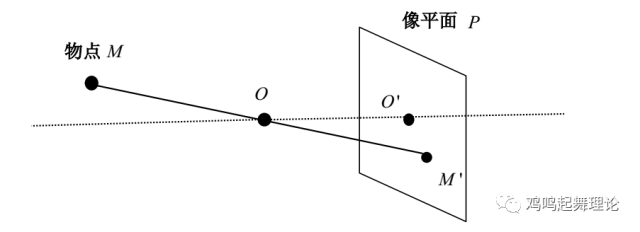
眼睛是灵敏的光学感觉器官,是一切动物与外界联系的信息接受器。众所周知人类依靠双眼可以感知现实世界:物体的颜色、距离、大小等。随着生物解剖学的发展,人们对人眼的生物结构及机能有了科学的认识。人眼是一个天然的高级光学系统。结构非常复杂。形象的说,人眼像一架自动摄像机,水晶体如同摄像机的物镜,能够在人的神经器官的控制下自动调焦,瞳孔如同光圈,视网膜如同相机底片,接受物体的 影像信息。人眼感知景深的机制给了人们启发。 经过研究发现由相机在两个不同的视角下拍摄的两幅图片,如果知道现实物点 P 在两幅图片中的对应关系, 就可以精确计算出 P 点的三维坐标信息。可以用针孔模型来近似描述相机的成像机制,如图所示。M 为现实场景中的一物点, O为相机的光心, O' 为光心在像平面上的投影, OO'为相机光轴,M '为物点 M 在像平面 P 上的像点。
针孔模型
为简单起见,考虑间隔适当距离、光轴平行的两相机(相机参数一致)【这是最理想化的双眼模型】,同一物点 M (为了讨论方便,假设物点 M 位于左相机的左边),在两个相机的成像如图所示。M1 为物点 M 在右侧相机像平面的像点, M2 为物点 M 在左侧相机像平面的像点, O1为右侧相机的光心, O2为左侧相机的光心。
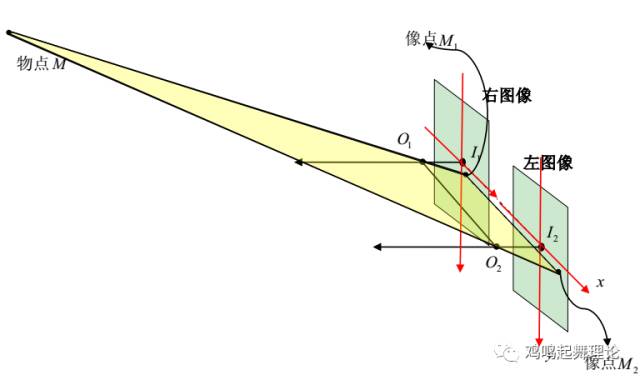
双目摄像机对点目标成像原理图
单独拿出上图的左右像平面来看,如下图所示。I1、 I2为左右像平面的中心(也即分别为左右相机的光心在像平面上的投影),分别以 I1、 I2为坐标中心建立坐标系。由几何知识可知O1O2 平行于 I1I2,记为O1O2 || I1I2, O1O2 || M1M2,所以M1M2 || I1I2 。
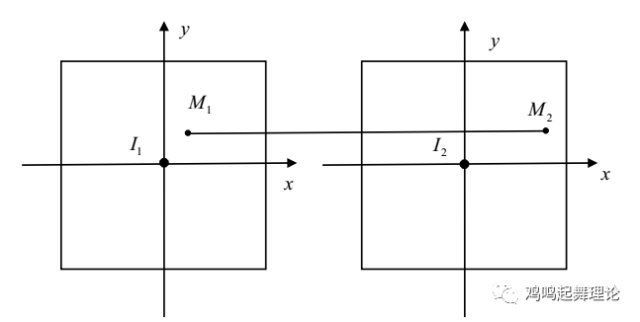
单点目标在双目摄像机左右视平面的成像
单独来看平面 MM1M2(上图中的阴影部分),易知 ∆MO1O2相似于∆MM1M2,所以,根据三角形相似原理:MO1/MM1 = O1O2/M1M2.
设 M1 、 M 2 在对应的像平面的横坐标分量别为 x1、 x2,则有:
M1M2 = I2I1 + x2-x1
如果定义两相机的光心之间的距离为基线距离,记为b=I1I2 ,(x2-x1)为同一物点在两个像平面上的视差,记为 d。则上式式可简化为:
M1M2 = b+d
则进一步进行公式推导:
MO1/MM1 = MO1/(MO1+O1M1) = b / (b+d)
可以简化为:
MO1/O1M1 = b/d
现在单独来看物点 M 与其在右侧相机的像平面的像点 M1 的对应关系。以右相机光心O1为坐标原点,如图示建立世界坐标系:
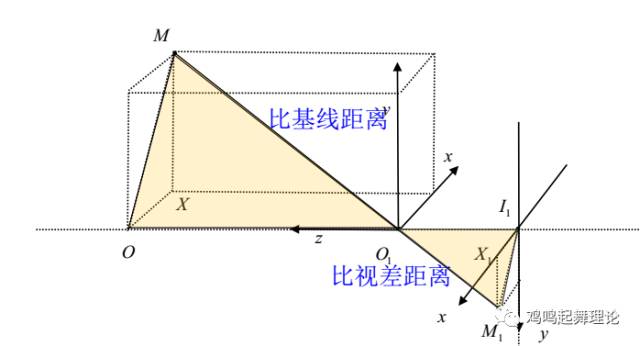
照相机成像坐标系与光心所在世界坐标系间的坐标变换关系
通过这张图像,我们很容易就可以得到,景深信息Z:
Z / O1I1 = MO1 / O1M1 = b / d (要知道O1I1是我们右侧摄像机的焦距啊亲!)
Z = (b*f)/d (f:摄像机的焦距)
由此,我们便可以恢复出目标的景深信息。
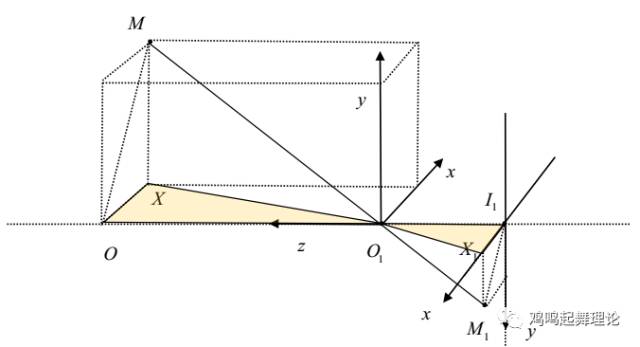
3.1 X坐标维度信息
X坐标三维恢复示意图
X/x1 = Z/f X = (x1*Z)/f
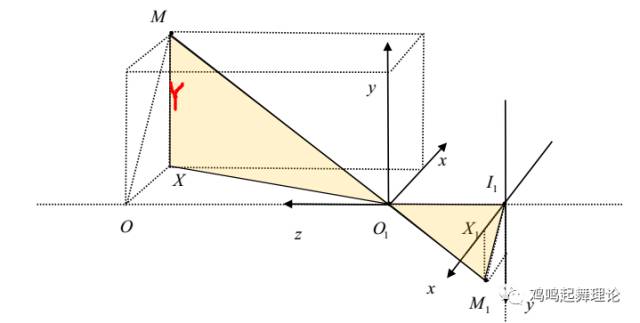
3.2 Y坐标维度信息
Y坐标三维恢复示意图
Y/y1 = Z/f Y = (y1*Z)/f
给定相机参数和在一定位置所拍摄的两幅双目图片,如何能够找出所有像点的两两对应关系?并求出相应视差?
只有得到图像上所有目标点的视差才能得到相片中每一个像点对应物点的三维坐标,这又是一项艰难的工作!
小白团队出品:零基础精通语义分割↓↓↓

交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~