来源：机器学习算法那些事

本文约2700字，建议阅读6分钟 
本文为你介绍常用 Normalization 方法的总结与思考。

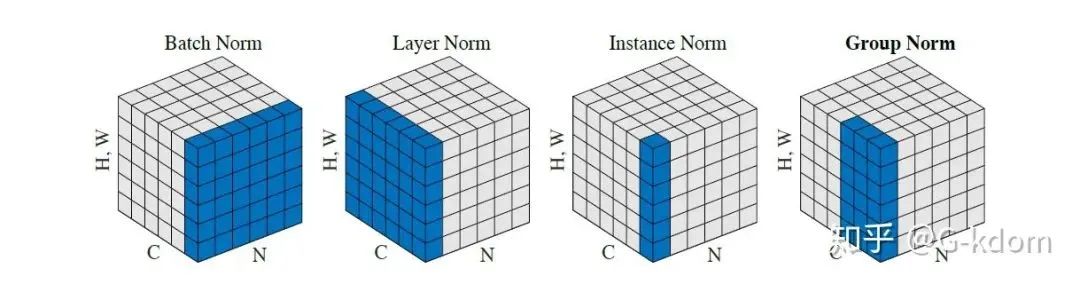
每个子图表示一个特征图，其中N为批量，C为通道，（H，W）为特征图的高度和宽度。通过蓝色部分的值来计算均值和方差，从而进行归一化。

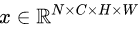如果把特征图比喻成一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 有W 个字符。

1. BN 求均值时，相当于把这些书按页码一一对应地加起来（例如第1本书第36页，第2本书第36页......），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求“平均书”的操作（注意这个“平均书”每页只有一个字），求标准差时也是同理。

一、 Batch Normalization, BN   

论文链接：https://arxiv.org/pdf/1502.03167.pdf

• 沿着通道计算每个batch的均值 

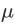
• 沿着通道计算每个batch的方差 

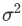
• 做归一化

• 加入缩放和平移变量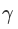和

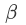
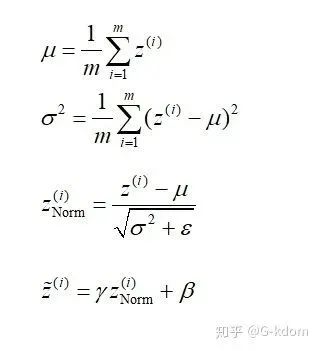
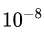其中 是一个很小的正值，比如 。加入缩放和平移变量的原因是：保证每一次数据经过归一化后还保留原有学习来的特征，同时又能完成归一化操作，加速训练。 这两个参数是用来学习的参数。

二、 Layer Normalization, LN

论文链接：https://arxiv.org/pdf/1607.06450v1.pdf

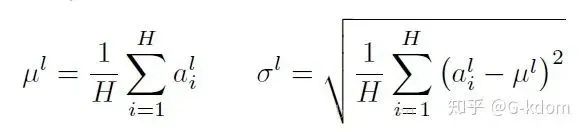
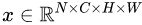对于特征图 ，LN 对每个样本的 C、H、W 维度上的数据求均值和标准差，保留 N 维度。其均值和标准差公式为：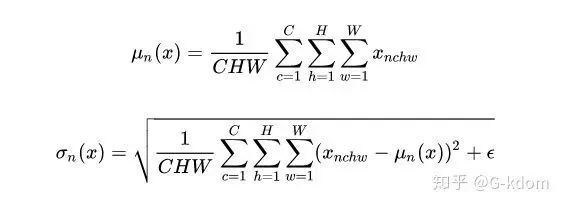

三、  Instance Normalization, IN

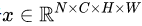对于，IN 对每个样本的 H、W 维度的数据求均值和标准差，保留 N 、C 维度，也就是说，它只在 channel 内部求均值和标准差，其公式如下：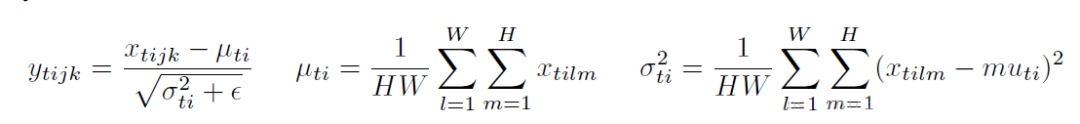

四、 Group Normalization, GN

GN的主要思想：在 channel 方向 group，然后每个 group 内做 Norm，计算 的均值和方差，这样就与batch size无关，不受其约束。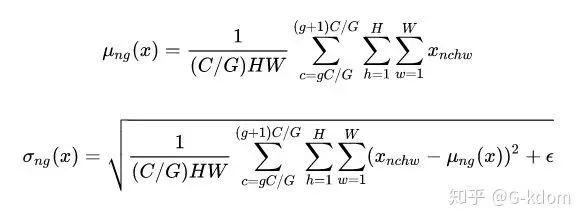

def GroupNorm(x, gamma, beta, G=16):
    # x_shape:[N, C, H, W]    results = 0.    eps = 1e-5    x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))
    x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)    x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)    results = gamma * x_normalized + beta    return results

总结

我们将feature map shape 记为[N, C, H, W]。如果把特征比喻成一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 有W 个字符。

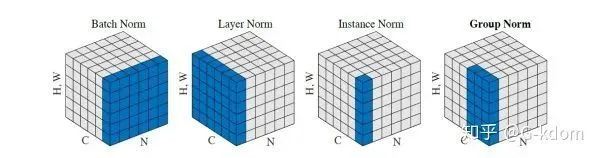
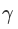另外，还需要注意它们的映射参数和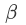的区别：对于 BN，IN，GN， 其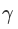和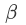都是维度等于通道数 C 的向量。而对于 LN，其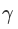和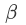都是维度等于 normalized_shape 的矩阵。