谁说Python慢来着？不用Python，这个问题难倒了无数的程序员-技术圈

（点击上方快速关注并设置为星标，一起学Python）

作者 | 天元浪子责编 | 欧阳姝黎
出品 | CSDN博客

围棋是全世界最古老的棋种（没有之一），也是古代哲学思想和中国传统文化的物质载体。小小纹枰，不过一尺见方，竟蕴藏着万千气象，着实令人为之着迷。少年时代的我，曾经有一段时间醉心于围棋。

标准的围棋盘由横竖各19道线组成网格，共有361个交叉点，每个交叉点上有白子、黑子和无子等三种可能的状态。那么问题来了：围棋总共有多少种不同的局面呢？

稍微思考一下，所有的程序员都会给出正确的答案：3^{361}（3的361次方）。可是，这究竟是一个多大的数字呢？算一下就知道了。

Python程序员随手写了一行代码，敲个回车，计算就结束了。

>>> pow(3,361)17408965065903192790718823807056436794660272495026354119482811870680105167618464984116279288988714938612096988816320780613754987181355093129514803369660572893075468180597603

C/C++程序员看完Python程序员的操作，不以为然，心里想，别看你写起来简单，速度肯定没我快。讲效率，还得看我C/C++的。

long result = 1int ifor(i=0; i<361; i++) {  result *= 3;}

写到这里，C/C++程序员忽然意识到，long int恐怕不够用，即使long long int也只有8个字节，最大只能到2^{64}-1计算3^{361}肯定会溢出的。比long long更大的整型没有了，要是临时定义一个结构保存超大整数，再为超大整数的计算写一堆函数，恐怕一时半会儿搞不定。这可如何是好？要不用改用double float试试？赶紧上网查了一下，double可以表示-1.79E+308 ~ +1.79E+308之间的任意数，可是3^{361}3在这个范围内吗？

这时，C/C++程序员心里有点慌了。幸好有点数学功底，简单计算一下:

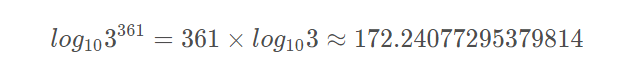
3^{361}大约有173位长，总算还在double覆盖的范围之内。也不用循环了，直接使用数学库中的pow函数吧。

#include <stdio.h>#include <math.h>
int main(void) {    double result = pow(3,361);    printf("%Lf\n", result);
    return 0;}

最后，C/C++程序员给出了一个浮点类型的答案。虽然精度略有损失，但也不算离谱。我用的是CodeBlocks，显示耗时28毫秒，这里面应当包括了编译连接的时间，否则C不至于慢到这个程度。

17408965065903191000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000.000000
Process returned 0 (0x0)Execution time : 0.028 s

看完C/C++程序员的这番折腾，Java程序员擦擦额头的冷汗，心中暗自庆幸：多亏我大Java有BigInteger这样的神器，不然真要出丑了。

import java.math.BigInteger;
BigInteger result = new BigInteger("1");for(int i=1; i<=361; i++) {    result.multiply(new BigInteger("3")));}

BigInteger用起来很方便，计算3^{361}毫无压力，只是不能兼容普通整型的那些运算符号，所有的运算都需要显式地调用函数，比如，这里的乘法就得调用multiply函数。

以上场景，纯属臆测，绝无褒贬任何编程语言之意，请各位明察。实际上，Python的超大整数计算也是C语言实现的，只不过采用了非常精妙的方案，最终经过各种优化，性能远超我们自己写出来的C代码。

Python的超大整数计算方案，精妙在哪儿呢？仅举存储一例：普通的Python整型采用4个字节存储，当处理超大整数时，每4个字节一个存储单元，单元之间采用2^{30}

即1073741824进制，一个单元满1073741824即向上一单元进位。

Python超大整数的存储实现

上图是超大整数1152921506754330627采用1073741824进制的存储示意图，占用了三个存储单元共计12个字节，每个单元仍然是普通的整型——这就是Python的超大整型和普通整型完全兼容的秘密。在这一点上，Python可以说完胜Java的BigInteger。不过Java还有个BigDecimal，可以无损地处理任意精度的浮点数，为Java扳回一局。

采用1073741824进制的Python的超大整数计算方案的效率如何呢？还是以计算3^{361}为例，看Python代码需要多长时间。

>>> import time>>> def power(x, base=2):  t0 = time.time()  result = pow(base, x)  print('耗时%.06f秒'%(time.time()-t0))  return result
>>> power(361, base=3)耗时0.000000秒17408965065903192790718823807056436794660272495026354119482811870680105167618464984116279288988714938612096988816320780613754987181355093129514803369660572893075468180597603

太神奇了！居然连1微秒都不到？我有点怀疑这个结论，继续测试更大的数字，2的1000次方。

>>> power(1000)耗时0.000000秒10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

计算2^{1000}所花时间同样少于1微秒，但是显示计算结果花费了较长时间。我把代码修改了一下，不再显示计算结果，只考察计算时间。

>>> def power(x, base=2):  t0 = time.time()  result = pow(base, x)  print('耗时%.06f秒'%(time.time()-t0))  #return result
  >>> power(10000) # 2的1万次方耗时0.000000秒>>> power(100000) # 2的10万次方耗时0.000000秒>>> power(1000000) # 2的100万次方耗时0.005016秒>>> power(10000000) # 2的1千万次方耗时0.048000秒>>> power(100000000) # 2的1亿次方耗时0.620648秒>>> power(1000000000) # 2的10亿次方耗时7.448035秒>>> power(10000000000) # 2的100亿次方耗时77.881435秒

计算2的1万次方和2的10万次，所花时间仍然不足1微秒。直到计算2的100万次方时，方才显示耗时5毫秒。当算完2的100亿次方之后，我没有继续下去——2的100亿次方，这个数字实在是太过恐怖，我已经无法想象它的大小了。要知道，地球上全部物质的原子数量，也不过是1.28E47这个量级，大约是2的157次方。

那么，Python能够计算的最大整数到底有多大呢？我没有明确的概念，不过我在验证费马小定理的逆命题时，出现过一次超大整数计算错误。

a = 2t = 2305843009213693951s = 1152921504606846975Traceback (most recent call last):  File "huge.py", line 56, in <module>    miller_rabin(x) # M61  File "huge.py", line 42, in miller_rabin    print((pow(a, t*pow(2,s)) - 1)%huge_num)MemoryError

当我试图计算pow(a, t*pow(2,s)时，发生了内存错误。这里a等于2，s大于115亿亿，t大于230亿亿。显然，这个结果远远大于2的100亿次方。

（完）