图像特征点、投影变换与图像拼接

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

一、全景拍照中的投影变换

在32. 镜头、曝光，以及对焦（下）中，我给你介绍了各种各样的相机镜头，也介绍了视场角（FOV）这个概念。现在咱们手机上的主摄像头一般FOV是七、八十度左右，有的更小一些。但人类的视觉系统FOV可以达到  。

广角镜头、鱼眼镜头能够让你拍摄出非常大FOV的图像。但它们非常昂贵，而且具有强烈的畸变。

全景拼接这个功能也能够让你拍摄出很大FOV的图像，你很可能已经使用过这个功能了，它甚至可以拍摄出水平FOV达到360o的图像。我们可以比较下。这样拍摄出来的图像比起鱼眼镜头的畸变小很多。

全景拼接是通过先拍摄不同视角的多张图像，然后将它们拼接而成的：

那么，像下面这样几个视角拍摄的图像，我们是不是直接拼接平移这些图像然后拼接就可以了呢？

很显然，不管我们是把左边的图像摆在上面，还是把右边的图像摆在上面，都会观察到“对不齐”的现象（看看中间栏杆的断裂缝）：

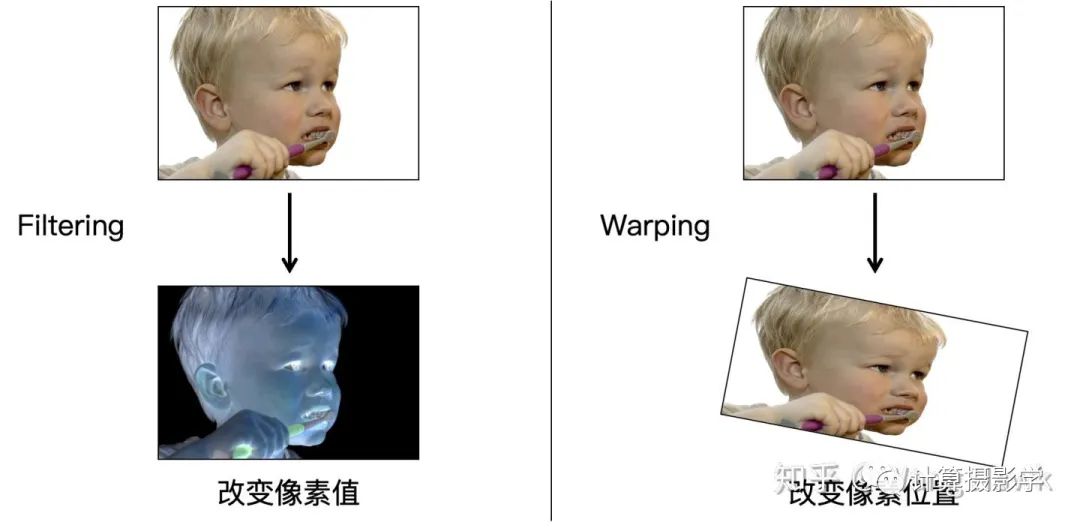
那应该怎么办呢？这时候就要用到我在28. 图像扭曲中介绍的图像的Warping技术。适当的Warp图像然后再做拼接，能够使得我们得到完美的全景图像：

Warping是一种改变图像像素位置的技术

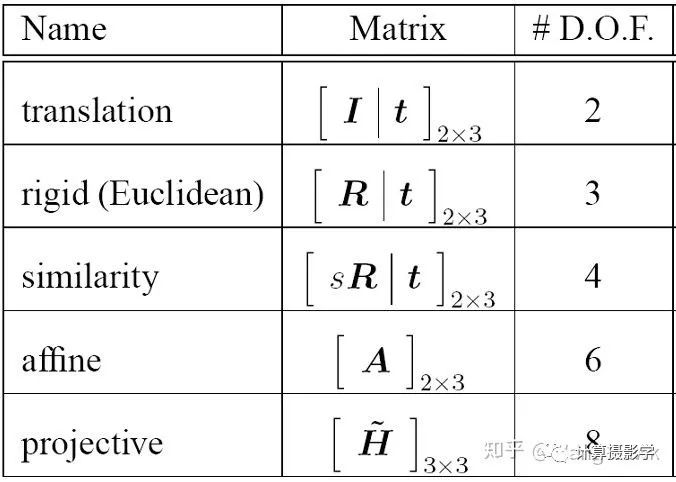
各种类型的2D图像变换都可以用变换矩阵来表示，如下图所示，其中包括平移变换(Translation)、刚体变换(Rigid)、相似变换(Similarity)、仿射变换(Affine)、投影变换(Projective)。

它们具有不同的内核和自由度：

那么，在全景拼接中我们用什么样的变换矩阵呢？事实上，此时我们通常采用的是投影变换，因为它的能力比起上面其他的变换形式都更强。下面是同样两张图像，三种不同变换形式的拼接结果，可以看到投影变换的结果是最自然正确的：

投影变换不仅仅用于全景拼接，我们还可以使用它来做视角变换，比如把正视图变换为俯视图或侧视图：

还可以用来模拟旋转视角：

校正多幅图像：

事实上，不仅仅是在数字图像处理时代人们使用投影变换，在平常的生活中人们早就在利用投影变换了。比如，你很可能了解甚至亲眼见过3D绘画，艺术家利用透视原理在地上作画，从而在某一个视角观看时可以有非常逼真的3D效果。这事实上是一种将2D图像反向变换为3D图像的过程。

艺术家也早就将投影变换应用到了画作中，例如下面这幅图左上角的人物脚下踩着的地面，就遵循投影变换中近大远小的规律。

而我们甚至可以反向利用投影变换，来看看他们脚下的图案的实际样子。可以想到画作作者倾注了多少心血在细节上：

文艺复兴时代投影变换刚刚被发现，所以类似上面的这种表现形式在那时候的画作中经常出现：

有一幅著名的油画叫做“大使们”，是画家小汉斯·霍尔拜因的作品。这幅画有非常多的解读，尤其是在画作前景有一个奇怪的、扭曲的物体：

可以利用反向投影变换将这个局部图像校正到正常的视角，原来是一个可怕的头骨：

事实上，还可以利用一些生活中常见的物体，例如一个勺子，来实现图像扭曲，从而理解画作中的物体。（将勺子靠近画作，勺子表面的曲面反射光线，从而可以让你看清画里面的物体）

二、什么时候可以使用投影变换

好了，你已经看到在绘画和全景拼接时，我们通常可以采用投影变换（又称为单应变换）来Warp图像，从而得到预期的结果。那么问题来了？投影变换在什么场景下适用，什么情况下不适用呢？

还是让我们看看29. 小孔相机的模型：

可以看到小孔成像时，物体方向的光线总是会通过共同的相机中心。这意味着拍照时，我们只是在用图像平面来选择部分光线。

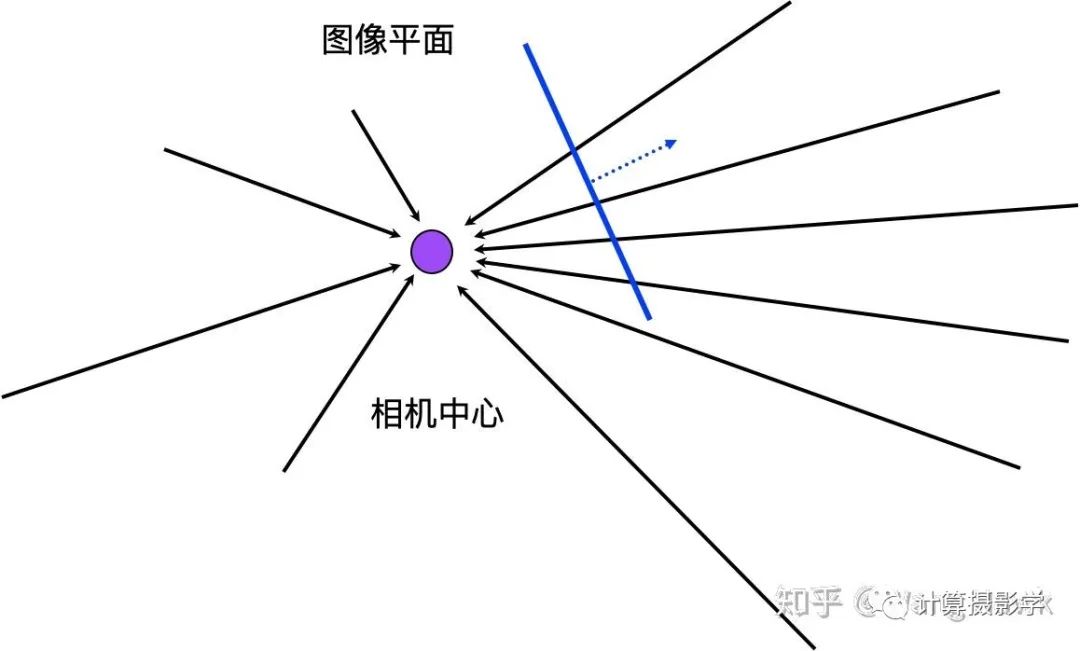
当我们用2D投影变换来讲图像变换到新的视角时，情况如下：

这里你可以看到，只要新的视角和原始视角有共同的光学中心，并且和原视角有共同的视线范围，就可以将原始视觉的图像利用投影变换变换到新的视角下。

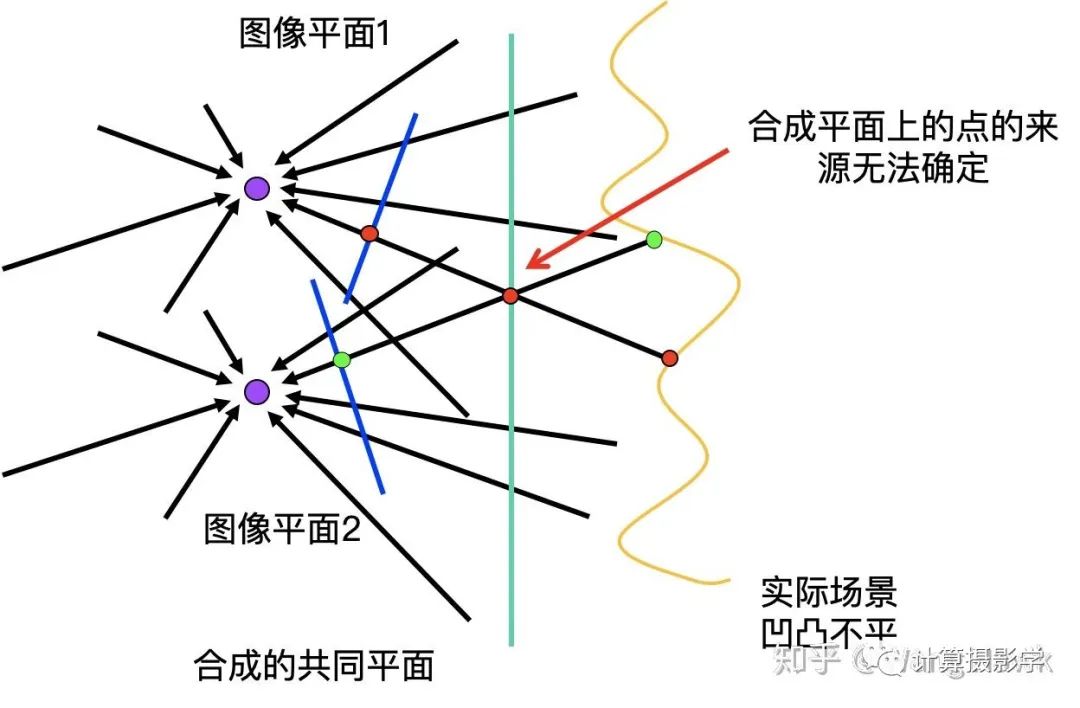
而在全景拼接中，假如我们要把在不同相机中心位置拍摄的图像通过投影变换拼接到一起时，会怎么样呢？比如下图，我们要将图像平面1和2通过投影变换到绿色线表示的共同平面上去，从而实现拼接，此时会怎样呢？

这个时候，你会发现合成平面上的点很可能会出现无法确定来源的情况，这实际上就是由于“视差”导致的。也就是说，在图像拼接时，2D投影变换（也称为单应变换）无法应对相机中心平移导致的视差现象。

但在少量的情况下，即便相机中心平移，也可以采用投影变换，如果：

如果你使用过微软的Onenote，或者“名片全能王”、“扫描全能王”这样的软件，你可以看到它们能比较好的将名片，或是照片等转换为正视图。其中也就利用了对平面物体采用投影变换的原理——特别要注意的是，采用这种方式，不需要知道实际相机的物理参数，纯粹采用2D图像变换即可做到。

三、投影变换矩阵的计算

投影变换矩阵，正如上面所讲，是一个3X3的矩阵，其中一共有8个自由度。一个图像上的点P变换到另外一个图像上的点P'的过程用下式来描述，其中H是2D投影变换矩阵，也称为单应矩阵。

将矩阵乘法展开可得：

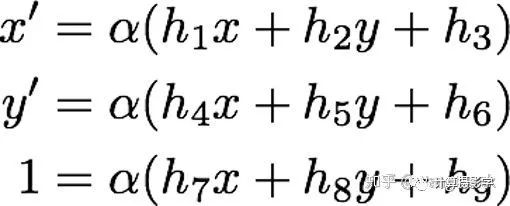
抛弃尺度量后有：

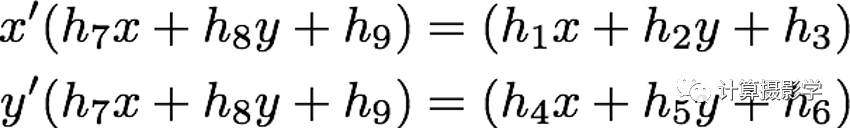
再稍加整理有：

所以如果知道原始图像和变换后的图像的一对对应点的坐标，可以构成两个线性方程。因此，如果要确定变换矩阵中的8个未知量，一共需要4对对应点，8个线性方程：

我们将上式写作矩阵和向量的乘法有：

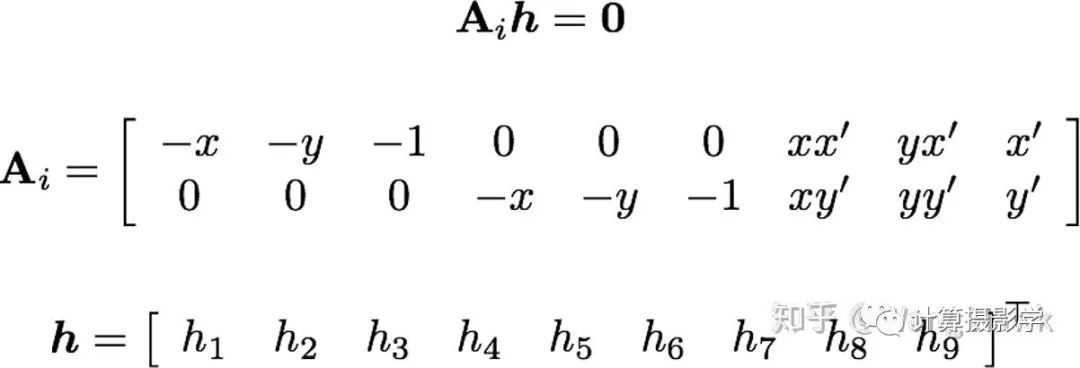
这样又多个对应点时，就成了：

这里的A可以是正定的（未知数==方程个数），也可以是超定的（未知数<方程个数)。可以简单的利用SVD分解来求解上述方程得到H，从而进行图像的变换。

在上面的过程中，我们忽略了获取不同图像视角对应点坐标的过程，事实上可以手动指定图像的对应坐标点来计算出单应矩阵。比如在“名片全能王”这样的应用中，就是通过检测到名片的四个角位置，然后指定屏幕上的名片框的四个角的位置，从而计算出单应矩阵并进行名片图像的变换的。

但是实际我们要做图像拼接的场景通常比名片更加复杂，没有可以轻易指定的边框角，有没有更智能的方法来获取图像间的对应点呢？这就是下一节所要讲的。

四、图像对齐时的特征点获取

正如上面所讲，要计算图像视角间的变换矩阵，需要确定图像的对应点的位置。那么什么样的点适合这个用途呢？我上面讲过名片全能王这样的应用采用的是名片的四角点，那么对于其他自然场景呢？

比如说上图，其中我们选择的点要求：

• 在两个视角中都很显著

• 在两个视角中都容易检测

• 不会和其他的点混淆

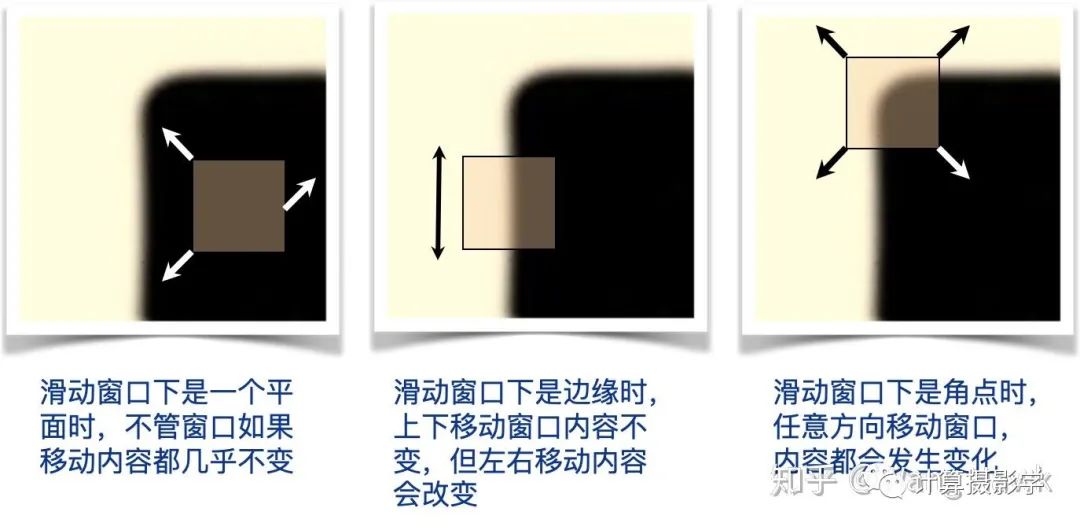
我们称这种点为”特征点“。有一种基础的，容易理解的特征点为”角点“，通过下图很容易可以理解：

有一种著名的角点检测算法是"Harris Corner”检测算法，其过程也非常容易理解：

稍稍解释下期中的关键步骤：

我已经在3. 数码相机内的图像处理-基本图像滤波中介绍过图像的梯度计算方法，而这里我们要求在一个很小的局部窗口内计算每个像素点的梯度值：

将梯度减去平均值，则是为了做一定程度的归一化. 利用这个归一化的梯度值，我们可以计算协方差矩阵，从而拟合一个抛物面（注意下图的P，代表梯度计算的局部图像块）

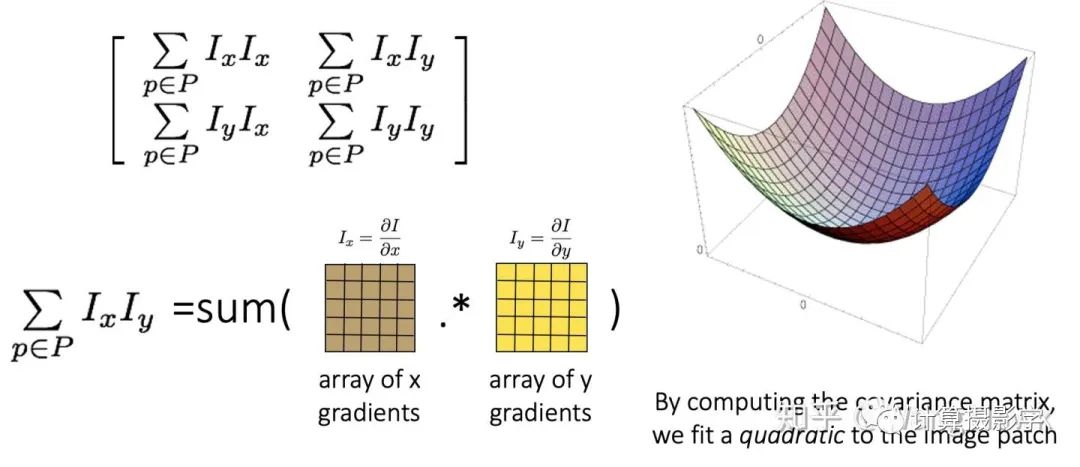
这个协方差矩阵的特征向量有着特殊的意义，它可以写作下式，从而反应出图像局部点的特点：

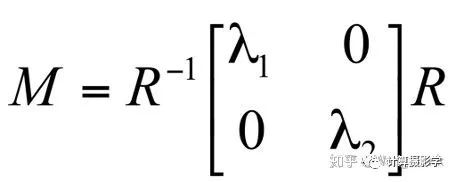
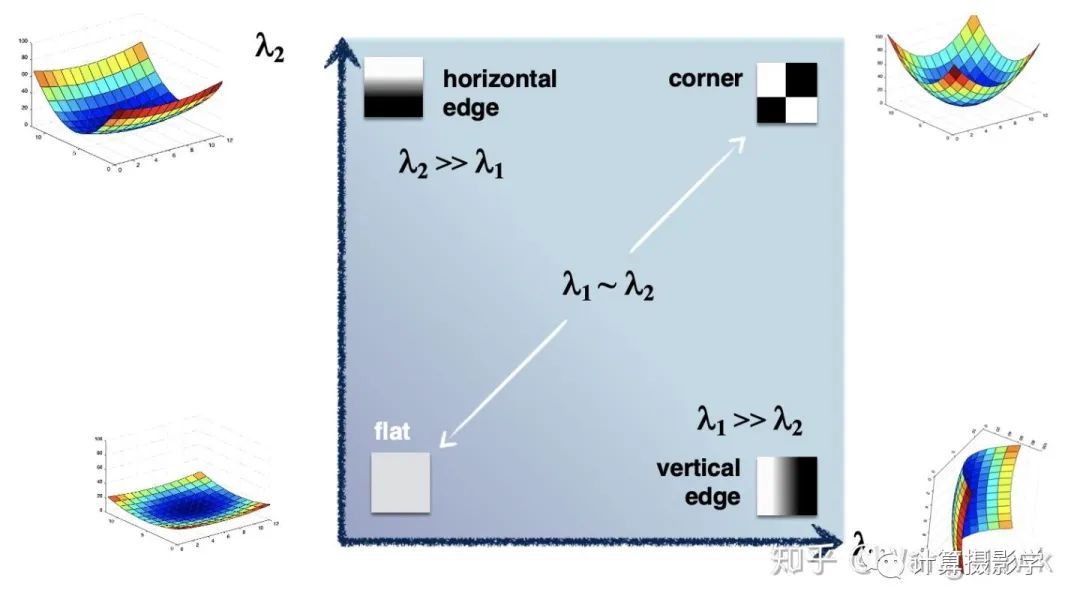
可以看到，只有两个特征值都比较大且没有明显的差距时，才是角点。因此可以通过  来确定是否是角点。更流行的方法则是通过下面的Harris角点检测算子来确定是否是角点，相比使用  这个算子计算量更小。

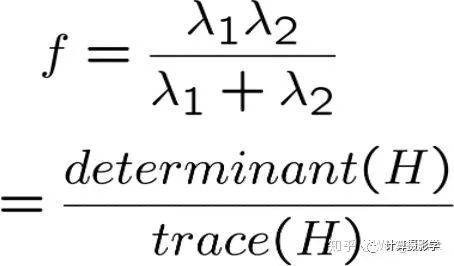
当然两者其实都很相似：

在实际使用时，会发现局部区域有大量点都满足算子>threshold的条件，因此还需要采用“非极大值抑制”的方法，选择局部区域算子最大的点作为最终的特征点。我们来实际看看在图像中寻找角点的过程：

五、总结

今天这篇文章从全景拼接开始，讲到了拼接中采用的2D图像变换主要是单应变换（投影变换），然后再讲了单应变换矩阵的直接计算方法。我们看到只需要知道至少4个非共线的点对就可以确定单应变换矩阵。最后讲了一种非常简单直观的获取图像特征点的方式——Harris Corner检测法。

事实上，图像的特征点检测还有很多高级的方法，你一定听说过像SIFT/SURF/ORB等方式，事实上从2003年SIFT的作者D.G.Lowe就另外一名大牛M. Brown合写了文章Recognising Panoramas，其中就用SIFT特征点来作为图像变换关系的计算基础。

由于篇幅原因，本文不再对此做展开，将来有机会时再深入探讨全景拼接中的高级方法。

六、参考资料

今天的主要参考资料为：

• CMU 2017 Fall Computational Photography Course 15-463, Lecture 19

• M. Brown and D. Lowe，Recognising Panoramas， 2003