【机器学习】降维代码练习
本课程是中国大学慕课《机器学习》的“降维”章节的课后代码。
课程地址:
https://www.icourse163.org/course/WZU-1464096179
课程完整代码:
https://github.com/fengdu78/WZU-machine-learning-course
代码修改并注释:黄海广,haiguang2000@wzu.edu.cn
Principal component analysis(主成分分析)
PCA是在数据集中找到“主成分”或最大方差方向的线性变换。它可以用于降维。在本练习中,我们首先负责实现PCA并将其应用于一个简单的二维数据集,以了解它是如何工作的。我们从加载和可视化数据集开始。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
data = pd.read_csv('data/pcadata.csv')
data.head()
| X1 | X2 | |
|---|---|---|
| 0 | 3.381563 | 3.389113 |
| 1 | 4.527875 | 5.854178 |
| 2 | 2.655682 | 4.411995 |
| 3 | 2.765235 | 3.715414 |
| 4 | 2.846560 | 4.175506 |
X = data.values
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1])
plt.show()
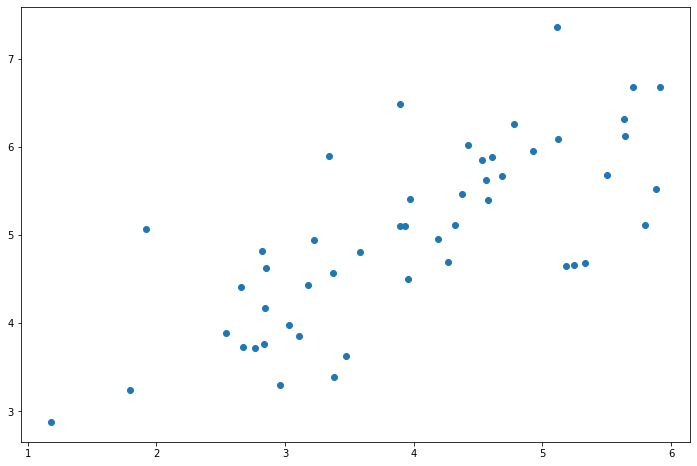
PCA的算法相当简单。在确保数据被归一化之后,输出仅仅是原始数据的协方差矩阵的奇异值分解。
def pca(X):
# normalize the features
X = (X - X.mean()) / X.std()
# compute the covariance matrix
X = np.matrix(X)
cov = (X.T * X) / X.shape[0]
# perform SVD
U, S, V = np.linalg.svd(cov)
return U, S, V
U, S, V = pca(X)
U, S, V
(matrix([[-0.79241747, -0.60997914],
[-0.60997914, 0.79241747]]),
array([1.43584536, 0.56415464]),
matrix([[-0.79241747, -0.60997914],
[-0.60997914, 0.79241747]]))
现在我们有主成分(矩阵U),我们可以用这些来将原始数据投影到一个较低维的空间中。对于这个任务,我们将实现一个计算投影并且仅选择顶部K个分量的函数,有效地减少了维数。
def project_data(X, U, k):
U_reduced = U[:,:k]
return np.dot(X, U_reduced)
Z = project_data(X, U, 1)
我们也可以通过反向转换步骤来恢复原始数据。
def recover_data(Z, U, k):
U_reduced = U[:,:k]
return np.dot(Z, U_reduced.T)
X_recovered = recover_data(Z, U, 1)
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(list(X_recovered[:, 0]), list(X_recovered[:, 1]))
plt.show()

请注意,第一主成分的投影轴基本上是数据集中的对角线。当我们将数据减少到一个维度时,我们失去了该对角线周围的变化,所以在我们的再现中,一切都沿着该对角线。
我们在此练习中的最后一个任务是将PCA应用于脸部图像。通过使用相同的降维技术,我们可以使用比原始图像少得多的数据来捕获图像的“本质”。
faces = loadmat('data/ex7faces.mat')
X = faces['X']
X.shape
(5000, 1024)
def plot_n_image(X, n):
""" plot first n images
n has to be a square number
"""
pic_size = int(np.sqrt(X.shape[1]))
grid_size = int(np.sqrt(n))
first_n_images = X[:n, :]
fig, ax_array = plt.subplots(nrows=grid_size,
ncols=grid_size,
sharey=True,
sharex=True,
figsize=(8, 8))
for r in range(grid_size):
for c in range(grid_size):
ax_array[r, c].imshow(first_n_images[grid_size * r + c].reshape(
(pic_size, pic_size)))
plt.xticks(np.array([]))
plt.yticks(np.array([]))
练习代码包括一个将渲染数据集中的前100张脸的函数。而不是尝试在这里重新生成,您可以在练习文本中查看他们的样子。我们至少可以很容易地渲染一个图像。
face = np.reshape(X[3,:], (32, 32))
plt.imshow(face)
plt.show()
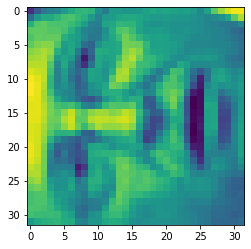
看起来很糟糕。这些只有32 x 32灰度的图像(它也是侧面渲染,但我们现在可以忽略)。我们的下一步是在面数据集上运行PCA,并取得前100个主要特征。
U, S, V = pca(X)
Z = project_data(X, U, 100)
现在我们可以尝试恢复原来的结构并再次渲染。
X_recovered = recover_data(Z, U, 100)
face = np.reshape(X_recovered[3,:], (32, 32))
plt.imshow(face)
plt.show()
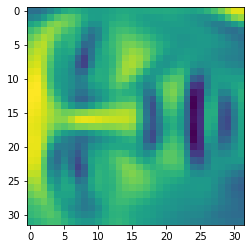
我们可以看到:数据维度减少,但细节并没有怎么损失。
参考
Prof. Andrew Ng. Machine Learning. Stanford University
