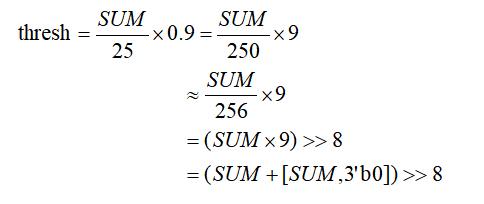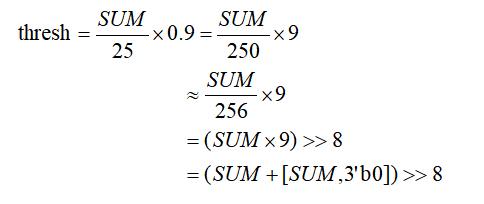首先,视频图像的采集与处理,最终无非是两个目的,或是供人查看审阅(视频录像、监控视觉等),或是供机器检测识别(二维码、车道线、物体姿态等检测)。对于人眼视觉,我们更关注图像的色彩、清晰度、分辨力等,更多的我们希望在画质上能够给人带来更加赏心悦目的感觉,所以手机很重要的一个指标就是拍照的效果——ISP,各家也都在ISP设计/Tuning上花精力,来提高产品的竞争力。但若是机器视觉,很多时候我们并不关心图像本身的色彩甚至灰度图像,而是具体的边缘轮廓等,比如二维码、车道线、运动检测、区域分割等,再比如循迹小车更关注的是路线的识别与跟踪,因此通常我们只需要二值化图像,最后再进行进一步的检测。
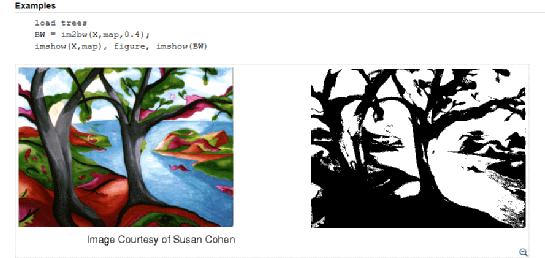
以上图为例,右图为左图的二值化结果,尽管存储容量降低到了1/24,但是仍然不耽误我们看整体形态,以及对数目的识别。
图像的二值化,是后续图像处理的基础,我们从彩色或者灰度图像上,获得二值化图像,然后在后续的图像算法中进行进一步的识别处理。图像二值化提取的质量,很大程度上决定了后续算法的效果与性能。那么,本章的核心,就是灰度图像的二值化处理算法的实现。这里由于篇幅的有限,前面全局阈值二值化的内容就不放出来了,我们直接进入进一步优化的主题:局部阈值二值化算法。
算法本身其实没有好坏,每一种算法都有其擅长的场景,相应的也有一些缺陷。
前面说的全局阈值二值化,对明暗均匀性比较好图像有一定的优势,并且计算量也很小。然而大千世界多姿多彩,图像场景明暗不一,我们采用全局阈值二值化针对所有场景,其效果不一定理想。进一步分析,图像像素在空域上是一个二维的分布,当前像素和其周边像素具有高斯特性的相似度,而离的相对较远的像素,其相干性就很小,甚至几乎可以忽略不计。但在进行全局阈值计算的时候,所有像素的权重都是相同的,这必然将引入很大的误差。采用以当前像素为中心的领域块去计算局部阈值,其结果的可信度往往比全局阈值二值化,要高的多。为此我随手拍一个明暗分明的图文场景,采用OSTU阈值二值化,以及采用5*5的局部阈值二值化,其结果对比如下,简直叹为惊止(详见代码Region_Binarization1.m):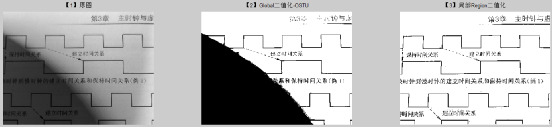
其中图一为真实场景中明暗分布的图片,采用OSTU全局阈值,其暗部的内容几乎全军覆没,而采用局部阈值的方式,其结果并不受到原始图像明暗的影响,相对较好的提取了图中的字符纹理。这也将是本节要介绍的重点:局部阈值二值化算法。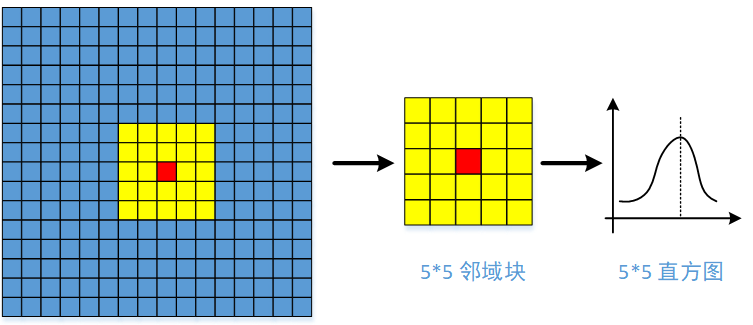
局部阈值二值化的核心思想,大致如上图所示。为了对红色像素进行二值化,我们需要知道红色像素邻域的阈值。这里假设采用5*5的邻域块,计算窗口内的阈值,然后根据阈值对红色像素进行二值化。
这里,如何计算窗口内像素的阈值,便成了局部阈值二值化的核心。类似全局阈值的计算,有以下几种方法:这里第一种又成了全局阈值二值化了,效果不理想;而第二种采用OSTU计算局部阈值,再遍历全图,这计算量比全局阈值还要大25倍,硬件不具备可实现性,软件也无比耗时。那么我们测试一下窗口内均值计算的方法,如下图所示,惨不忍睹:
从上图分析,确实我们在暗处也把纹理给提取出来了,但是同时也引入了很多的脏点。明明原本空白区域,多出了很多莫名其妙的异常点。我们假定5*5窗口内,没有文字图案,只有白色的纸张背景,那么25个像素必然在其均值附近分布,所以直接采用均值进行二值化,必然会有一些低于阈值的黑点产生。但这实际相对有效的纹理而言,这只是略微波动的背景噪声而已,不该被当作有纹理图案提取。要解决这个问题,我们需要一个容错的机制,或者说把这个条件稍微放宽一点,比如低于这个计算的阈值的一定比例,才算是有效的纹理。那么我们引入一个对阈值进行缩放的参数(这里主要是缩小),结合前面5*5区域计算均值进行局部阈值二值化,相关Matlab代码如下所示(详见region_bin_auto.m):% 灰度图像布局自动二值化实现
% IMG为输入的灰度图像
% n为求阈值的窗口大小,为奇数
% p为阈值的缩放
function Q=region_bin_auto(IMG,n,p)
[h,w] = size(IMG);
Q = zeros(h,w);
win = zeros(n,n);
bar = waitbar(0,'Speed of auto region binarization process...'); %创建进度条
for i=1 : h
for j=1:w
if(i<(n-1)/2+1 || i>h-(n-1)/2 || j<(n-1)/2+1 || j>w-(n-1)/2)
Q(i,j) = 255; %边缘像素不计算,直接赋255
else
win = IMG(i-(n-1)/2:i+(n-1)/2, j-(n-1)/2:j+(n-1)/2); %n*n窗口的矩阵
thresh = floor( mean(mean(win))) * p;
if(win((n-1)/2,(n-1)/2) < thresh)
Q(i,j) = 0;
else
Q(i,j) = 255;
end
end
end
waitbar(i/h);
end
close(bar); % Close waitbar.
核心代码主要是n*n窗口内的均值计算,我们累加后计算均值,再乘上了一个缩放的参数,得到最后n*n窗口内的阈值,再通过比较得到二值化后的图像。此时我们对比缩放前局部阈值二值化的结果,如下图所示,脏点已经被去除,但文字图案被很好的提取了出来:
见证了局部阈值二值化的优势,我们再来扒扒局部阈值二值化的劣势。上图中,我们在5*5的窗口内,进行局部阈值的计算。但如果是更大或者更小的字符,5*5窗口是否还可以得到较好的结果,请看下图: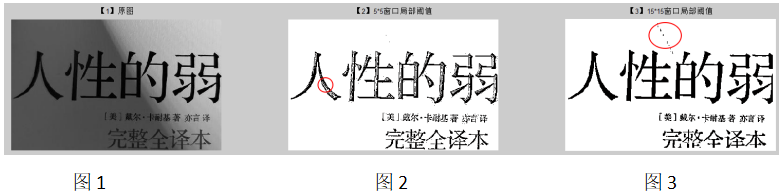
上图中,图2采用5*5的窗口进行局部阈值二值化计算,字符中间有被镂空,同时也出现了零星的脏点,这主要是窗口太小,覆盖在边缘与字体时,陷入了局部最优,无法计算得到合理的阈值。而图3采用15*15的窗口进行局部阈值的计算,由于窗口足够大,不会出现局部最优,很好的解决了图2的bug。1)但这也引入了一个问题,如图3圈圈所示,在明暗相间的区域,采用较大的窗口,错误的将分界线当作了图案纹理。并且15*15窗口,进行全图遍历阈值的计算,这个计算量也不小,所以,算法并没有严格的对与错,想要做到真正的局部阈值自适应,还是有一定的难度。
在前面高斯滤波中,我们采用行缓存,以流水线的方式实现5*5的滤波操作。这里我们的局部阈值二值化算法,其实现流程和5*5的高斯滤波基本一致,仍然是一种通用的滑窗计算方法。
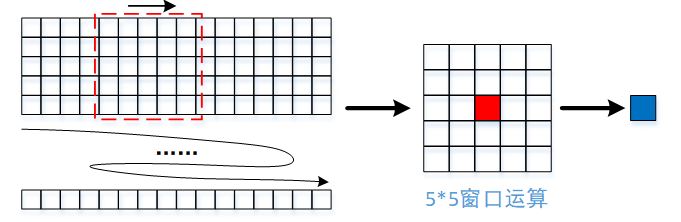
如上图所示,在FPGA中采用行缓存,实现流水线5*5窗口的获取,再采用流水线进行均值的计算,以及结合一定的缩放,得到最后的阈值,最后通过比较得到最终的二值化数据。这里相对5*5高斯滤波,只是多了如下几步操作,其核心实现方法还是一样的:2)对均值进行缩放,上述Matlab代码主要是缩小3)对采用2)值作为阈值,比较得到结果,而非直接替代最后输出因此在FPGA开发中,我们可以基于前面5*5高斯滤波的RTL代码,计算均值,并继续流水线方式进行2)3)的操作即可。主要流水线流程如下所示:
这里的均值涉及到了浮点操作,假设以缩放p=0.9为例,我们需要做一定的转换,如下所示,我们巧妙的结合除法再乘以浮点的操作,通过放大及近似的方法,将其转换为加法/移位操作,其中最后一步还可以直接去高8bit代替移位操作,节省LUT。