用 SVD 修改马氏距离及其应用
马氏距离(Mahalanobis distance)、高斯分布、奇异值分解(SVD)以及主成分分析(PCA)有内在联系。本文用一个简单的示例来揭示这层联系并且掌握它的实际应用。
1装备
library(ggplot2)
library(ggthemes)
c(R.version$os, R.Version()$version.string)
'linux-gnu'
'R version 3.6.1 (2019-07-05)'
2数据和内置函数
假设我们采集了一批共 16 个人的身高、体重数据,先把它们放入一个数据框。
hw <- data.frame(Height.cm=c(164, 167, 168, 169, 169, 170, 170, 170, 171, 172, 172, 173, 173, 175, 176, 178),
Weight.kg=c( 54, 57, 58, 60, 61, 60, 61, 62, 62, 64, 62, 62, 64, 56, 66, 70))
首先,我们先用最简单的方法来检测离群值。将那些离平均身高或平均体重超过两个标准差的点标记为离群值/异常值。
is.height.outlier <- abs(scale(hw$Height.cm)) > 2
is.weight.outlier <- abs(scale(hw$Weight.kg)) > 2
pch <- (is.height.outlier | is.weight.outlier) * 16
plot(hw, col=c("#56B4E9"), pch=pch)
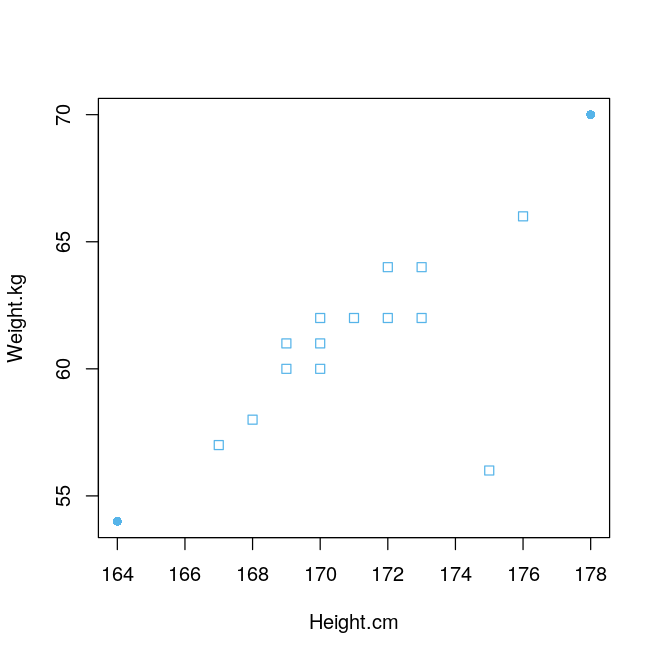
上图中实心点是所谓的异常值,然而,(175,56) 这个人明显偏瘦,直觉上很明显它应该是个异常值,可是上面的方法并没有检测出来。从散点图也可以看出来它偏离了正常点。
为了能够把它检测出来,我们不妨换个思路。换什么呢?换距离的计算方式。
我们先用 R 语言内置的计算马氏距离的函数 mahalanobis 来求解。
# 将离中心马氏距离最大的 3 个点选出来作为异常值
n.outliers <- 3
m.dist.order <- order(mahalanobis(hw, colMeans(hw), cov(hw)), decreasing=TRUE)
is.outlier <- rep(FALSE, nrow(hw))
is.outlier[m.dist.order[1:n.outliers]] <- TRUE
pch <- is.outlier * 16
plot(hw, col=c("#56B4E9"), pch=pch)
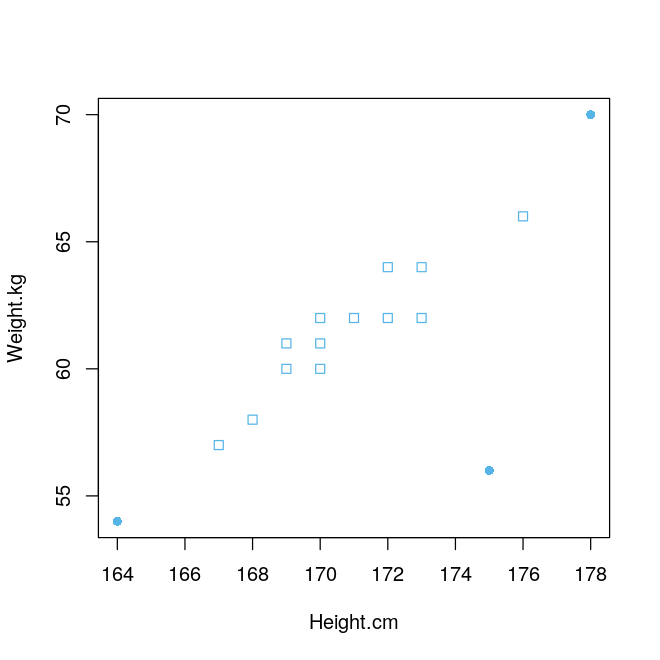
上图中实心的三个点被当作异常值,终于把那个离群点找出来啦。我们来看看内置函数计算出来的 16 个马氏距离到底是多少。
md <- mahalanobis(hw, colMeans(hw), cov(hw))
md
4.28192150772506
1.42890278811573
0.817645979562166
0.391759215459851
0.716013317982929
0.104756509429368
0.168876910394913
0.541756085090398
0.115869320988084
0.70286576627966
0.0713659019290032
0.408245827913156
0.519478289148748
12.4242733195133
2.04308127482557
5.26318798564204
发现没有,那个点的马氏距离确实是最大的,换句话说,它是最不合群的,这完全符合我们的直觉。
下面用本人最爱的 ggplot2 来展示一下上面检测到的异常值。
hw$isoutlier <- is.outlier
# 看看最后三行
tail(hw,3)
| Height.cm | Weight.kg | isoutlier | |
|---|---|---|---|
| 14 | 175 | 56 | TRUE |
| 15 | 176 | 66 | FALSE |
| 16 | 178 | 70 | TRUE |
sp <- ggplot(hw, aes(x=Height.cm, y=Weight.kg, color=isoutlier)) +
geom_point(size = 2) +
theme_economist() +
stat_ellipse(geom="polygon", aes(fill = isoutlier), alpha = 0.25, show.legend = FALSE, level = 0.95)
sp + scale_color_manual(values=c("#56B4E9", "#fF5600"))
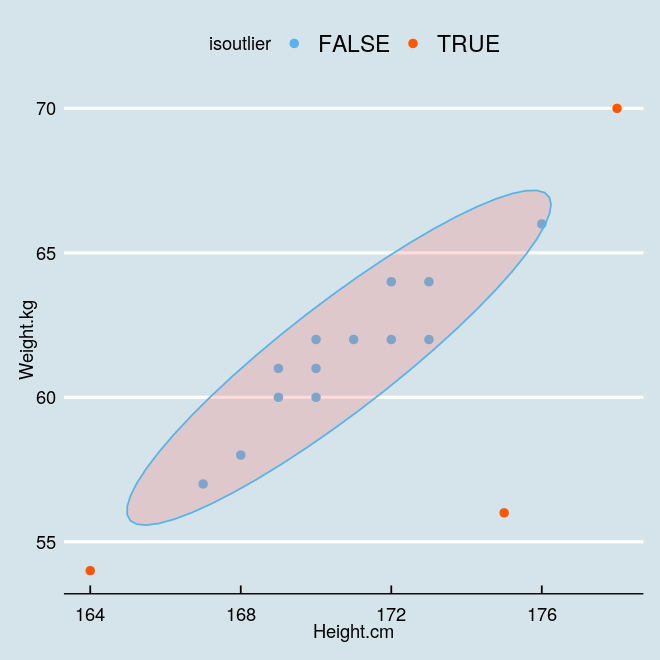
3手动计算马氏距离
马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(Mahalanobis)提出的,表示点与一个数据分布之间的距离。该数据分布的特征在于均值和协方差矩阵,因此被假设为多元高斯模型。协方差矩阵给出了数据在特征空间中分布的形状。
我们熟悉的欧氏距离有时有明显的缺点。它将样品的不同特征之间的差别等同看待,这一点有时不能满足实际要求。例如,在教育研究中,经常遇到对人的分析和判别,个体的不同属性对于区分个体有着不同的重要性。
因此,为了考虑不同特征的不同重要性,需要考虑协方差。下面我们直接从公式入手。已知矩阵的奇异值分解,
从而协方差矩阵的逆为,
点
其中,
注意,最后算出来的距离我们不开方,主要是为了跟 R 中内置马氏距离的计算保持一致。
.直接计算协方差矩阵
直接调用 R 内置的求协方差矩阵的函数 cov 以及 solve 函数来求逆矩阵,很容易得到跟内置马氏距离一样的结果。
X <- as.matrix(hw)
mhlbs <- function(X){
X_m <- scale(X,scale=F)
cov_mat <- cov(X_m)
cov_mat_inv <- solve(cov_mat)
md <- X_m %% cov_mat_inv %% t(X_m)
return(diag(md))
}
md = mhlbs(X)
md4.28192150772506
1.42890278811573
0.817645979562166
0.391759215459851
0.716013317982929
0.104756509429368
0.168876910394913
0.541756085090398
0.115869320988084
0.70286576627966
0.0713659019290032
0.408245827913156
0.519478289148748
12.4242733195133
2.04308127482557
5.26318798564204
.用 SVD 计算协方差矩阵
下面我们调用函数 SVD 来计算奇异值分解,再用右奇异向量和奇异值计算协方差矩阵的逆矩阵,最后求解马氏距离。
mhlbs_ <- function(X){
X_m <- scale(X,scale=F)
duv <- svd(X_m)
m = nrow(X_m)-1
W_inv <- duv$v %% diag(c(duv$d[1]^-2, duv$d[2]^-2)m) %*% t(duv$v)
md <- X_m %% W_inv %% t(X_m)
return(diag(md))
}
md = mhlbs_(X)
md
4.28192150772506
1.42890278811573
0.817645979562166
0.391759215459851
0.716013317982929
0.104756509429368
0.168876910394913
0.541756085090398
0.115869320988084
0.70286576627966
0.0713659019290032
0.408245827913156
0.519478289148748
12.4242733195133
2.04308127482557
5.26318798564204
没问题,计算结果也完全一致。
.改写异常值检测算法
上面例子中,除了马氏距离最大的那个离群点外,排在后面的两个点其实从身高体重的线性关系来看很正常啊,一定意义上来说不应该算作异常点。那么我们如何进一步修改距离的计算方式呢?
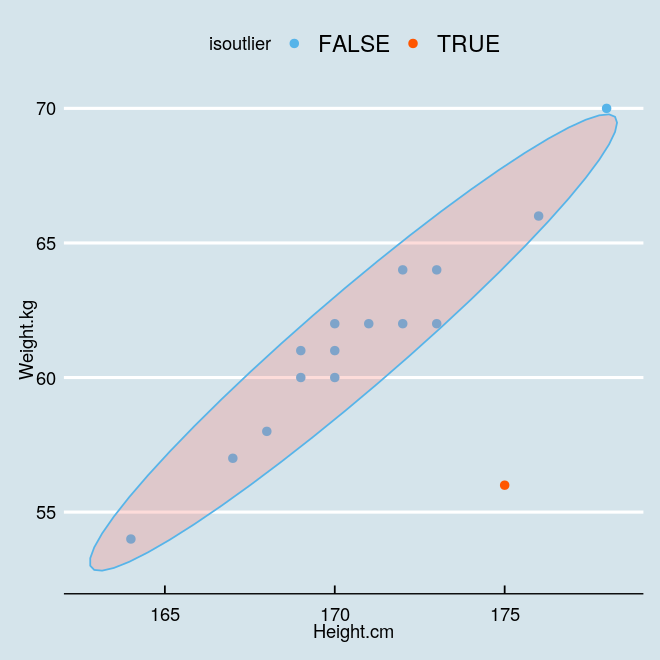
仔细观察马氏距离的计算公式,其实这里跟主成分分析(PCA)也有一定联系,相当于各个主方向上的度量不同(拉到文章开头看那个图片)。不妨这样想,沿上面第一个主方向上的延展不能算作异常,但是沿着垂直它的方向上可以认为是偏离航道了。因此,我们可以抛开第一个主方向,从第二个主方向来计算距离。
我们将第一个奇异值直接设成 0,这样相当于在计算距离的时候只考虑在第二个主方向上投影了。
mhlbs_v <- function(X){
X_m <- scale(X,scale=F)
duv <- svd(X_m)
m = nrow(X_m)-1
W_inv <- duv$v %% diag(c(0, duv$d[2]^-2)m) %*% t(duv$v)
md <- X_m %% W_inv %% t(X_m)
return(diag(md))
}
md = mhlbs_v(X)
md
0.113077461308034
0.0303515411319775
0.0144478656822281
0.183201236142446
0.623876699037339
0.000147961696133197
0.139877849888957
0.541461970704508
0.102390279273269
0.394139960952248
0.00919132026124367
0.261865093668431
0.0449225849552972
12.3515068432501
0.0973078250450808
0.0922335070027004
可以看到,此时那个离群点真的鹤立鸡群了,人群中一眼就能揪出来了吧。我们这里简单点,用平均值就能把这个点分割出来。
md > mean(md)
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
TRUE
FALSE
FALSE
hw$isoutlier <- md > mean(md)
# 看看最后三行
tail(hw,3)
| Height.cm | Weight.kg | isoutlier | |
|---|---|---|---|
| 14 | 175 | 56 | TRUE |
| 15 | 176 | 66 | FALSE |
| 16 | 178 | 70 | FALSE |
sp <- ggplot(hw, aes(x=Height.cm, y=Weight.kg, color=isoutlier)) +
geom_point(size = 2) +
theme_economist() +
stat_ellipse(geom="polygon", aes(fill = isoutlier), alpha = 0.25, show.legend = FALSE, level = 0.95)
sp + scale_color_manual(values=c("#56B4E9", "#fF5600")).其他应用
还根据马氏距离作判别问题,即假设有 n 个总体,计算某个样品 X 归属于哪一类的问题。此时虽然样品 X 离某个总体的欧氏距离最近,但是未必归属它,比如该总体的方差很小,说明需要非常近才能归为该类。对于这种情况,马氏距离比欧氏距离更适合作判别。
.缺点
但是请注意,如果所考虑的数据集中变量之间的关系是非线性的,那么用马氏距离也可能检测不到最明显的异常值。如下面例子,
my.dataframe <- data.frame(x=c(4, 8, 10, 16, 17, 22, 27, 33, 38, 40, 47, 48, 53, 55, 63, 71, 76, 85, 85, 92, 96),
y=c(6, 22, 32, 34, 42, 51, 59, 63, 64, 69, 70, 20, 70, 63, 63, 55, 46, 41, 33, 19, 6))
percentage.of.outliers <- 10 # Mark 10% of points as outliers
number.of.outliers <- trunc(nrow(my.dataframe) * percentage.of.outliers / 100)
m.dist <- mahalanobis(my.dataframe, colMeans(my.dataframe), cov(my.dataframe))
m.dist.order <- order(m.dist, decreasing=TRUE)
rows.not.outliers <- m.dist.order[(number.of.outliers+1):nrow(my.dataframe)]
is.outlier <- rep(TRUE, nrow(my.dataframe))
is.outlier[rows.not.outliers] <- FALSE
pch <- is.outlier * 16
plot(x=my.dataframe$x, y=my.dataframe$y, col=c("#56B4E9"), pch=pch)
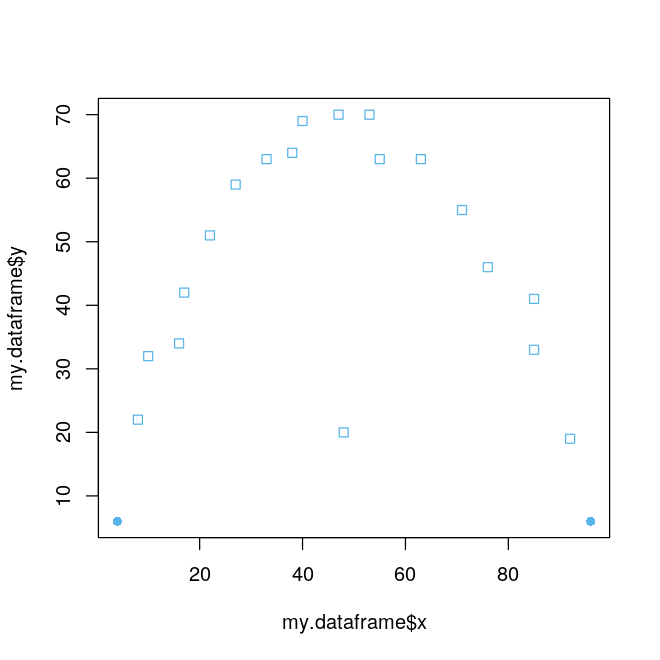
本篇使用了 R 语言,但如果要用 Python 来改写也很方便,有兴趣的话可以照着上面代码改一改。
⟳参考资料⟲
Matrix Algebra: https://www.statmethods.net/advstats/matrix.html
[2]Peter Rosenmai: https://eurekastatistics.com/using-mahalanobis-distance-to-find-outliers/