重磅！如何做到相机高精度标定？

点击下方卡片，关注“新机器视觉”公众号

重磅干货，第一时间送达

还记得当年的华南虎照片事件吗？我们能否从相机成像的原理来分析得知那是个纸板老虎？相机标定为什么能够达到小于0.01像素误差的精度？单相机能进行三维测量吗？这篇文章的下半部分里，将介绍与这些问题相关的知识。

  Ⅰ 前言  

时间过得好快。自从完成了这篇关于高精度相机标定的文章的上半部分以来，两个多月过去了。这两个多月，我每天忙忙碌碌地做着各种工作，这其中也有一些相机标定的工作。转眼已经11月，美国各大商店也早已摆满了节日相关的商品。于是我蹬开被窝，决定把这下半部分写完，这样今年年底以前还能够有空完成下一篇文章。

在上半部分里，我描述了针孔成像的原理、相机成像的模型、以及相机标定的基本原理。在这下半部分，我将介绍相机标定的具体实施和几个基本的应用。

  Ⅱ 相机的成像与标定模型回顾  

首先，我们回顾一下相机成像的数学模型。这个基于小孔成像的模型使得给定一个世界坐标系中的点，可以通过理论上的计算来得到它成像后在图像中的位置：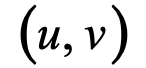

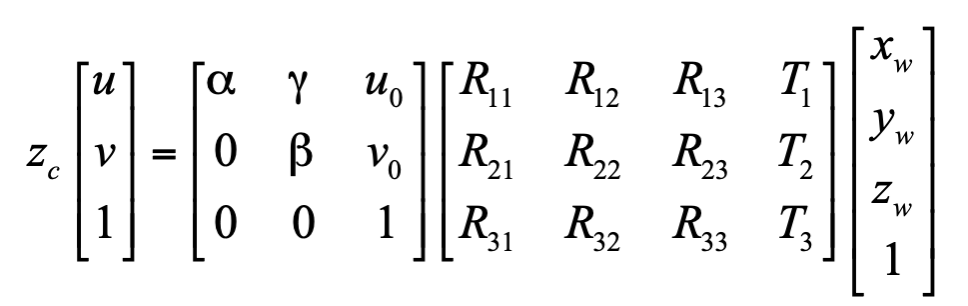
当考虑镜头畸变时，这个模型要分解为以下三步：

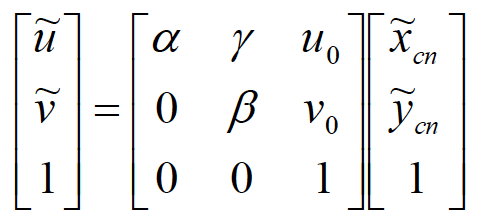
显然，相机的标定就是把这个数学模型中涉及到的参数确定下来。这些参数包括

• 18个内参数：

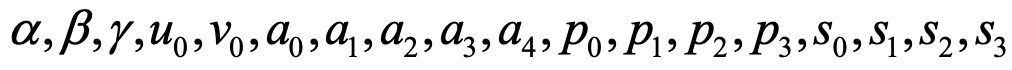
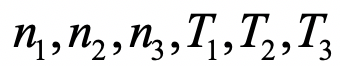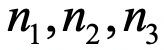• 6个外参数：。其中决定了9个转动参数。

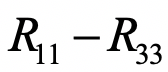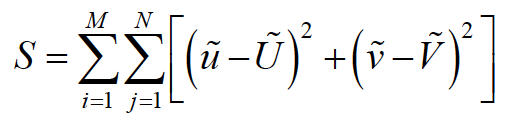
这里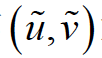，和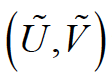分别是模型函数求得的标识控制点的像素坐标和实际图像中检测到的像素坐标。

基于以上分析，我们可以看到，相机标定的关键步骤有两点：（1）精确地得到相机采集到的标定板图像中标识控制点的像素坐标位置；（2）运用迭代的方法来获取相机的内外参数。

  Ⅲ 相机标定的实施  

 ·图像中标识控制点的位置获取 

如前所述，目前最常用的标定板图像有两种：棋盘格图案和圆点（环）图案。通常情况下，使用圆环图案能得到比使用圆点和棋盘格图案更高的精度。此外，同心圆环的个数可以超过2个。为了尽可能提高准确度，圆心的位置可以按照以下步骤来检测：

采用上面所述的方法再加上一些优化手段，相机标定的标识控制点的再次投影误差可控制在0.01像素以下，相比之下，最常用的OpenCV相机标定库和MATLAB相机标定工具箱只能得到0.1像素左右的误差。

 ·标定过程的算法实施 

Levenberg-Marquart非线性最小二乘算法是一种简单而非常强大的算法，它本质上是把高斯-牛顿算法和梯度下降算法结合了起来。大家如果没有用过，有时间的话可以自己写代码试一下。当然，如果实在觉得自己一行行地写这个相机标定优化的代码有难度，还有一个方法就是使用谷歌的开源库Ceres Solver以及相关的开源相机标定代码。现在，无论采用哪种方案，大家应该可以轻松搞定高精度相机标定了吧？！

其实事情还没有那么简单。原因是Levenberg-Marquart算法给出的是局部最优解，而不一定是全局最优解。为了解决这一问题，我们必须在迭代之前赋给标定参数们一些可靠的初始值。在所有的内参数中，我们其实只需要初始化α和β，其它的参数除了u0and v0设为图像宽度和高度的一半之外，一律设为0即可。当然，外参数是需要全部初始化的。

那么，如何初始化呢？其实也不难，但是具体的推导过程会需要一些篇幅。我建议大家去读一下Elan Dubrofsky的硕士论文[1]和张正友的那篇经典文章[2]，就可以了！

此外，前面其实忽视了一个技术细节，就是关于旋转矩阵和它相应的旋转向量。它们之间的互相转换，没什么难度。但是迭代算法所需要的相关求导，推导起来会让人有些头大。纵然不能一一列出推导过程，但本着严谨求实又简单快捷的科研精神，我把初始化和旋转矩阵相关的关键公式列在这里。我相信如果你了解了Levenberg-Marquart算法，又读了前面所提到的相关文章，是能够看到这些公式的有用之处的！

旋转矩阵对旋转向量的导数：

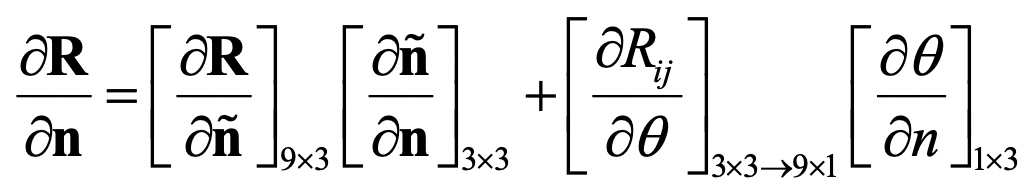
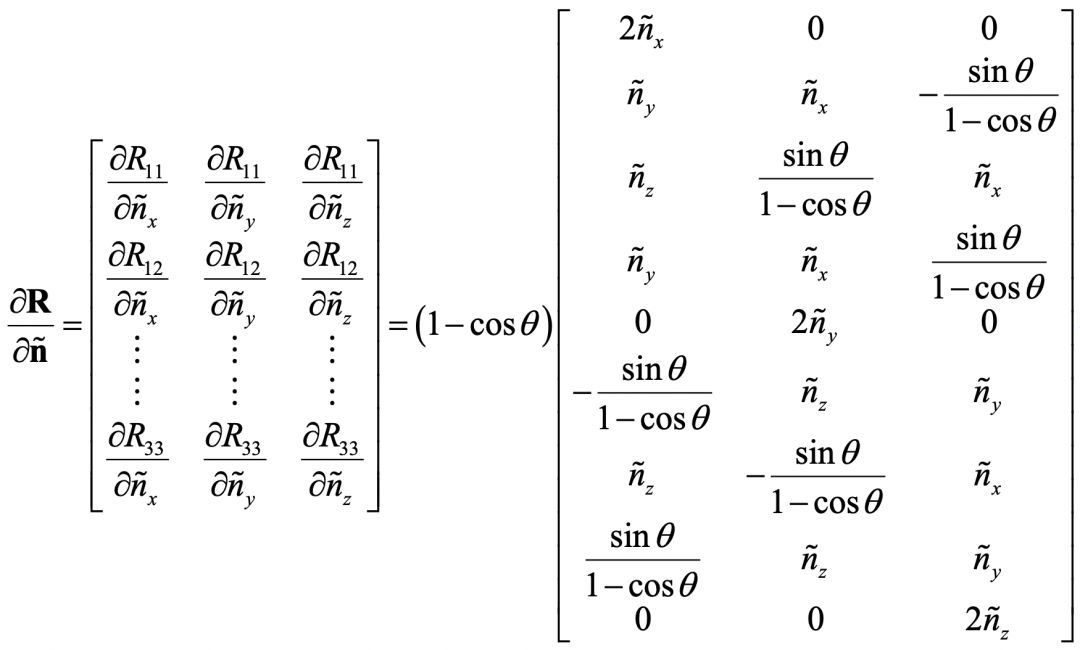
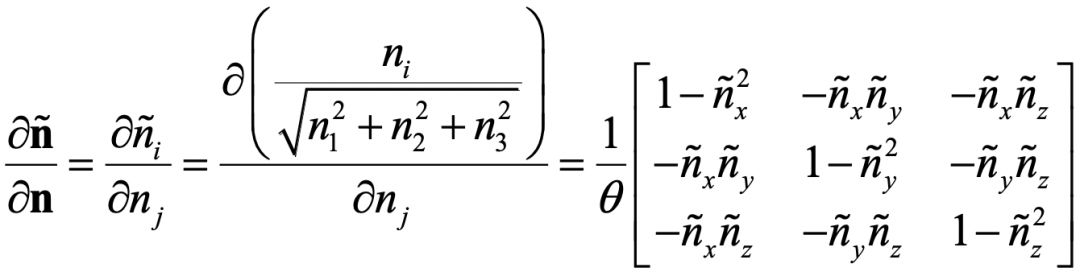
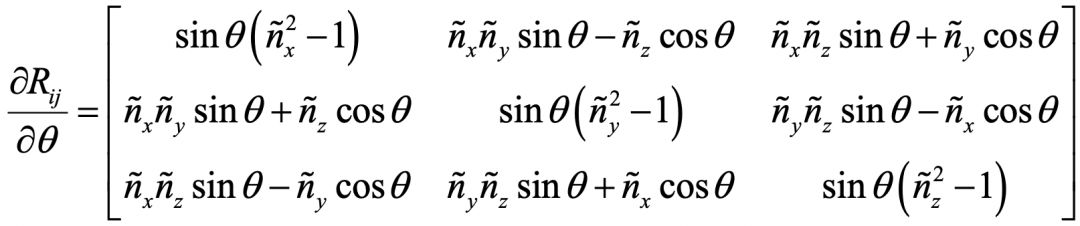
内参的初始化公式：

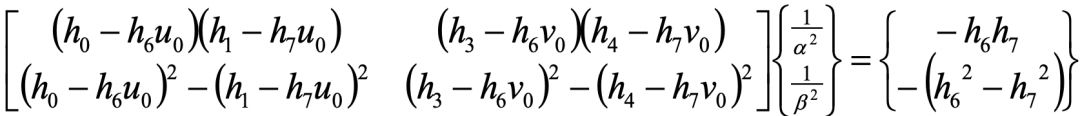
其中

H的计算以及实际编程中对一些变量的正则化，参考一下前述的文献就一目了然了。

外参的初始化公式：

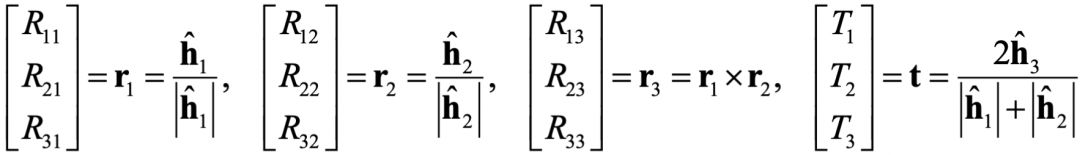
其中h的计算与上面的H类似，继续参考一下文献即可。

下面的动图，显示了上述相机标定的过程。

*高精度相机标定的步骤演示

  Ⅳ 相机标定的扩展  

得益于使用圆环图案、利用模板匹配更新圆心位置、以及使用复杂的镜头畸变模型等措施，上述的相机标定方法在实测中可以达到再次投影误差在0.005-0.01像素的范围内。而在后续的三维成像应用中，可以容易地帮助三维成像达到微米级的精度。但是，上述的相机标定的一个主要缺陷是它依赖于使用带标定图案的标定板。在小尺度视野的相机标定中，尚可以使用光刻的微小标定板和变更的成像模型来实现标定。而在稍大尺度视野下的相机标定中，可以使用编码的标定图案，因为图案是可以随意放置的，如下图所示的几块标定板可以同时且随意地放在视野中。

*编码的标定图案可以用来在较大视野下的相机标定

然而，在超大的视野下，采用标定板的相机标定方法是不可行的。如下图中对水坝位移的监测应用。关于这种情况的高精度标定方法，我将在接下来的几篇文章中有介绍，请耐心等待。

*采用标定板的相机标定方法在超大视野应用中是不可行的

  Ⅴ 相机标定的几个基本应用  

到此，相信大家已经清楚相机标定是怎么回事和怎么实施了。如果还有不明白的地方，就请把这篇文章的上下两部分再仔细读一遍。如果还需要帮助，那就......

但是，事情还没有结束。

既然我们花了这么长的篇幅介绍高精度相机标定，那就索性再多介绍一点儿关于相机标定的基本应用。比如，看下面这张几周前国庆70周年阅兵的一个镜头。假设相机或者摄像机是标定过了的话（注：这个标定其实属于超大视野标定），我们能够得到什么额外的常规相机不能提供的信息呢？

*国庆70周年阅兵现场的一个镜头

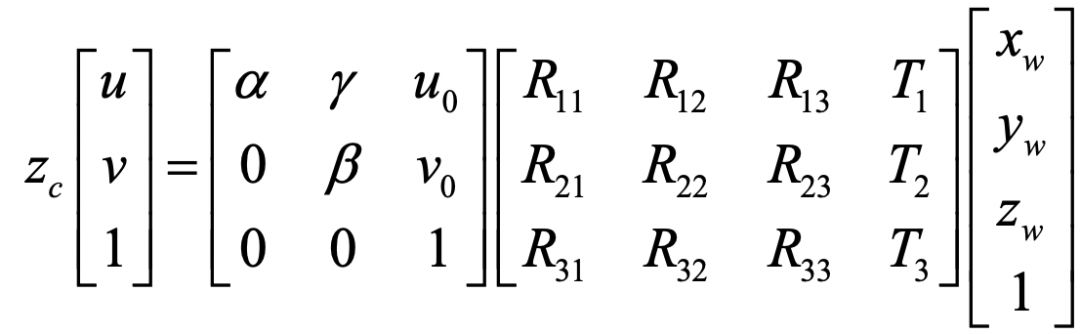
当我们拿到一幅由已经标定过的相机拍摄的照片后，对于照片中每一个基本单元—像素，上面公式中有四个未知量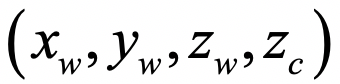：。方程有几个？只有三个！这就意味着我们是不能解得那四个未知量的。这倒也符合我们的常识：单凭单个相机是不能用来做三维成像的。接下来，问题来了。我们本着爱钻研的精神，想：能不能引入一些额外信息，使得方程可解呢？答案是肯定的。

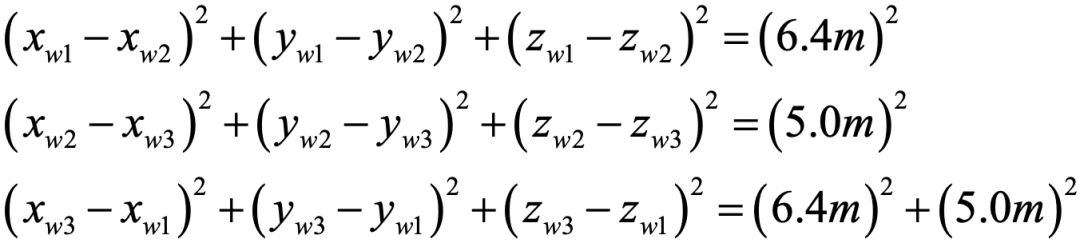
完美！因为现在我们有12个未知量和12个方程，问题可以解决了！也就是说，我们是可以通过解方程来得到画像的三维坐标的。即便画像在图像中不是正对着相机而是倾斜的，也没有问题。另外，我们也可以得到其它的一些信息，比如拍摄者距离天安门有多远。这个例子在当前的热门领域—网售和物流—是有重要应用的，它可以检测商品和包装盒的姿态来配合机械臂进行分拣。

在写上面单相机进行三维测量的过程中，我想起了多年前的华南虎照片一事。相信大家都知道此事，实在不知道怎么一回事的就百度一下吧。这件事情的核心，就是陕西省安康市某村一个叫周正龙村民，从年画上复印了一张老虎的图片，再贴到纸板上并立到草丛中，然后在几米到10米不等的距离处拍了几十张照片。之后，宣称自己拍摄到了濒危动物野生华南虎。一出闹剧之后，陕西省政府正式通报，照片中的老虎其实是纸板老虎。

*曾经轰动一时的周正龙所拍摄的“华南虎”照片

我提这件事情的原因是想给大家出一道“作业题”：根据周正龙所拍的一系列照片，虽然我们不能去标定当时的相机，通过本篇文章所介绍的知识，你能否通过计算分析得出那个老虎是个平面老虎？

让我们再回到四个未知量和三个方程。现在假设我们有两个相机，在共同的世界坐标系下标定后，那么对于物体或场景中的任何一个实际点来说，如果它能同时出现在两个相机分别拍摄的照片中，总共就有五个未知量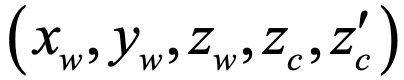：和六个方程。也就是，未知量居然比方程数还少一个！毫无疑问，问题是可解的。这也就是我们常说的立体视觉。例如下图中的人脸三维成像。

*使用双相机的人脸三维成像

当然，这种基于双相机的三维成像有一个难点：左右图像的匹配。也就是对于一幅图像中的一个像素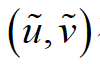，必须在另一幅图像中找到对应的另一个像素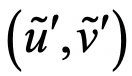。为了使匹配容易，一些产品例如苹果手机的三维人脸成像传感器、英特尔的RealSense三维测量传感器，都会采用红外的点结构光来辅助图像的匹配。关于这个话题，我将在以后专门写一篇文章。

事情到这里，细心的读者也许会有一个疑问：我们既然“一不小心”把未知量数目减少得比方程数目多了从而使得事情变复杂了—也就是需要左右图像的匹配，那么我们能否把未知量数目增加一个回去，从而使得匹配的问题变简单呢？

答案是可以的。比如我们只匹配水平方向的像素，那么未知量的数目是六个：，结合六个方程，问题是可解的！可是，怎么实现呢？

这时，有的读者也许会马上想到：Image Rectification 呀!不错，Image Rectification正是只匹配了一个方向！不过遗憾的是，如果这个Rectification的方案可行，那么有了图像后，马上解方程好了，根本不再需要做任何匹配。而那个Middleburry数据库和评估网站也可以马上关掉了。显而易见，这个方案是有问题的。至于原因，就再留给大家思考好了！

可行的方案是什么呢？请允许我继续卖个关子，鼓励大家思考一下好了。在本篇结束之前，趁机给大家一个提示：下面这一段基于高精度相机标定而进行的三维成像，正是采用了此方案。

*基于高精度相机标定进行的三维成像

本文已经接近结束，我也该拉上被窝了。文中提到的三个问题，你是否有了答案？为了拖更，这些答案我们下一次再公布吧。如果读者在阅读过程中有疑问，可以关注我们公司的公众号留言进行交流，我们稍后也会推出技术论坛和技术交流群，方便大家相互交流相互学习。

参考文献：

[1] Elan Dubrofsky,Homography Estimation, Master's thesis, University of British Columbia, (2009)http://cseweb.ucsd.edu/classes/wi07/cse252a/homography_estimation/homography_estimation.pdf

[2]  Z. Zhang, "A flexible new technique forcamera calibration'", IEEE Transactions on Pattern Analysis and MachineIntelligence, Vol.22, No.11, pages 1330–1334, 2000.http://research.microsoft.com/en-us/um/people/zhang/Papers/TR98-71.pdf