光照不均匀图像分割技巧1——分块阈值-技术圈

点击上方“程序员大白”，选择“星标”公众号

重磅干货，第一时间送达

前言
在数字图像处理中，图像分割是很关键的一步，当图像质量较好，光照很均匀的时候只需用全局阈值的方法就能很完美地完成图像分割任务，但是有些时候会遇到光照不均匀的现象，这个时候就需要用一些技巧才能达到比较好的分割效果，本文要介绍的是一种通过分块阈值进行分割的方法。

实例
在进入正题之前，我们先看一个实例，下面图1和图3为做硬币面额识别拍摄的，可以看到，由于硬币表面的反光以及打光角度的原因，图片存在严重的光照不均现象。
如果对两幅图像直接进行全局阈值可以得到图2和图4的结果，可以看到分割的效果很差，比如第一幅，右上角的光照要强一些，而且右上角的硬币存在一定的反光，灰度值整体偏高，导致最后分割效果很差。第二幅则是左边部分光照太强，左边的硬币分割效果很差。
本文将用分块阈值的方法解决这一问题。

图1 光照不均匀图像1 图2 全局阈值处理结果

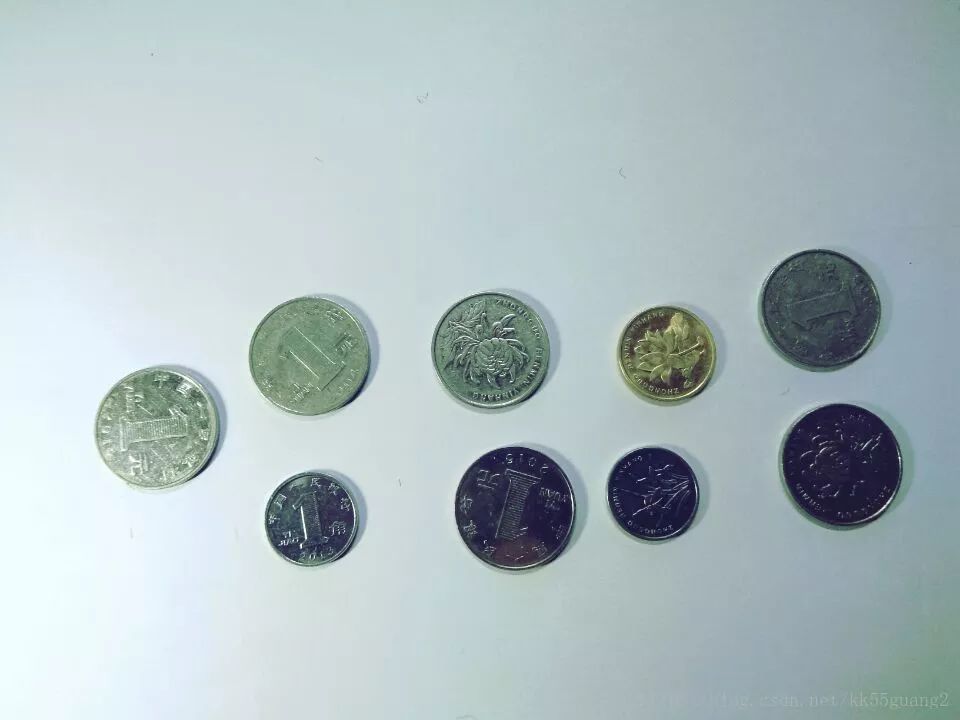
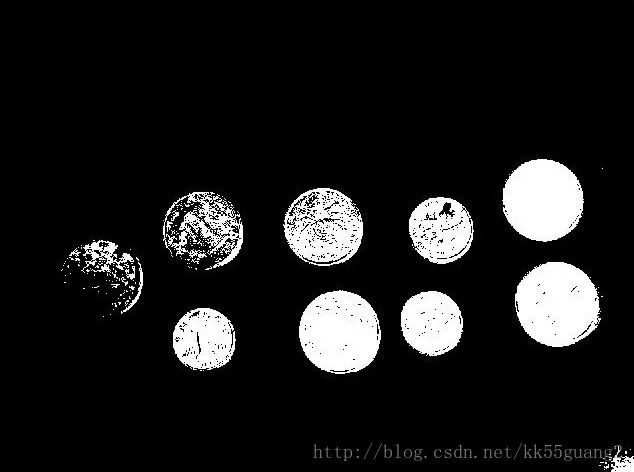
图3 光照不均匀图像2 图4 全局阈值处理结果

分块阈值思路
通过将图像分割成若干块，分别进行阈值分割，可以在一定程度上解决光照或反射造成的不均匀影响。选择的块要足够小，以便每个块的光照都近似均匀的，这样自动阈值时，在高灰度区域就会用高阈值分割，在低灰度区域就会用低阈值分割。
图5为分块结果，示例中分块与硬币大小相当，分完块之后就可以按块进行全局阈值法（这里采用常用的最大类间方差法，otsu法）处理了，但是需要注意的是有的块中只有背景，这个时候需要进行判断，排除对这种块的处理。
对于这种块的判断，笔者尝试过用otsu方法中提到的可分性度量：

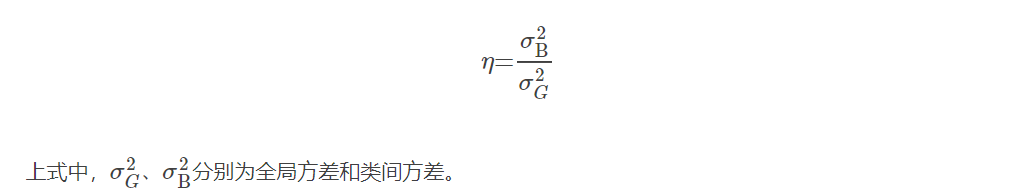
笔者在计算出各个块的可分性度量之后，发现区分效果并不是很好，后来通过分析最大类间方差法，有个想法就是用分割阈值处的类间平均灰度差判断图像块的可分性，当图像中只有背景或只有物体时，由于灰度值比较接近，则用otsu法算出的“背景”和“前景”平均灰度差（类间灰度差）会很小，类间平均灰度差 Δm 的数学表达式如下：

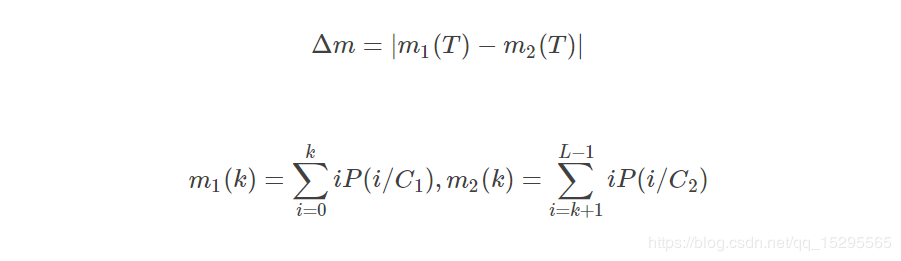
如图5中各块标注的文字所示，T为分割阈值，d为类间平均灰度差，可以看到当块中只有背景时，平均灰度差与有物体时相差很大，选取特征区分效果很好。本示例中，选灰度差20就能将两种不同的块很好的区分开。

图5 分块情况

之后仅对既有物体又有背景的块进行自动阈值处理、二值化、填充孔洞，可以得到图6的结果，可以看到每个硬币都被很好的分割出来

图6 分块阈值处理结果

代码

%功能：对一副图像进行分块阈值，可解决光照不均分割不足的问题%通过判断类间灰度差以排除纯背景或纯物体的干扰%作者：wikiwen%日期：2017/10/24%平台：matlab R2014clc,clear;close all;rn=5;cn=5;I = rgb2gray(imread('d.jpg'));[R , C]=size(I);%分别返回行和列数rblk=R/rn;cblk=C/cn;%小块的行数和列数x = 0:cblk:C;y = 0:rblk:R;M = meshgrid(x,y); %产生网格N = meshgrid(y,x);  %产生网格imshow(I);hold onplot(x,N,'r'); %画出水平横线plot(M,y,'r'); %画出垂直竖线T = zeros(rn,cn);dif = zeros(rn,cn);J = false(R,C);%初始化二值图X = uint8(zeros(rblk,cblk));%分块阈值，并判断类间灰度差以排除纯背景或纯物体的干扰for r=1:rn    for c=1:cn        r0=rblk*(r-1)+1;r1=rblk*r;        c0=cblk*(c-1)+1;c1=cblk*c;        X = I(r0:r1,c0:c1);        T(r,c) = graythresh(X);        [h,~] = histcounts(X,0:255);        T_int =uint8(T(r,c)*255);        dif(r,c) = graydiffer(h,T_int);%计算类间灰度差的函数略        str = ['T=',num2str(T_int),' d=',num2str(dif(r,c))];        text(c0+cblk/4,r0+rblk/2,str,'color','black');%显示信息        if dif(r,c)>20            J(r0:r1,c0:c1) = ~im2bw(X,T(r,c));        end    endendJ = imfill(J,'holes');%填充孔洞figure;imshow(J)

%功能：计算一幅图像前景和背景类间平均灰度差%输入：直方图数据h,分割阈值T%输出：类间平均灰度差%作者：wikiwen%日期：2017/10/26function[differ] = graydiffer(h,T)s1 = sum(h(1:T));s2 = sum(h(T:255));n1 = 1:T;n2 = T:255;u1 = double(n1)*h(1:T)' / s1; %背景灰度均值u2 = double(n2)*h(T:255)' / s2; %前景灰度均值differ = uint8(u2-u1);end

推荐阅读
13个你一定要知道的PyTorch特性
解读：为什么要做特征归一化/标准化？
一文搞懂 PyTorch 内部机制
张一鸣：每个逆袭的年轻人，都具备的底层能力

关于程序员大白

程序员大白是一群哈工大，东北大学，西湖大学和上海交通大学的硕士博士运营维护的号，大家乐于分享高质量文章，喜欢总结知识，欢迎关注[程序员大白]，大家一起学习进步！