浅谈Union-Find并查集
Union-Find并查集作为一种树型的数据结构,用于高效进行不相交集合的合并、查询
基本原理
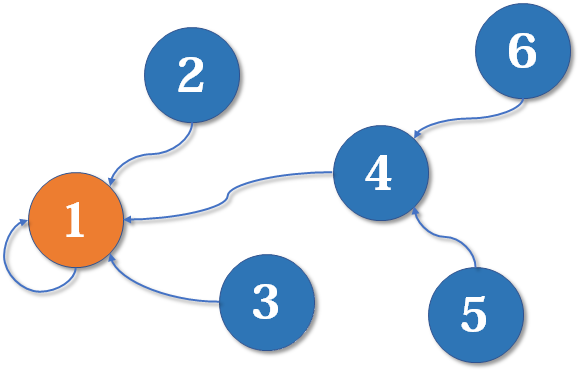
并查集的基本思路是用一个数组表示整个森林,其中树的根节点唯一标识了一个集合。当我们搜索找到了某元素的的根节点时,就能确定其所属的集合。顾名思义,对于一个并查集而言,其支持的操作方法自然包括:union、find。前者用于对指定的两个元素建立连接,将二者归属为一个集合,即所谓的属于同一个连通分量;后者用于查找指定元素所在连通分量的标识。同时如果期望判断两个元素是否存在连接,即判断并查集中的两个元素是否存在于同一个连通分量。则可以通过find方法进行实现。具体地,分别查询两个元素的连通分量标识,然后判断是否相同即可。并查集常见的API操作,如下所示
// 建立p节点、q节点之间的连接
public void union(int p, int q);
// 获取p节点所在连通分量的标识
public int find(int p);
// 获取连通分量的数量
public int getCount();
// 判断两个节点是否存在于同一个连通分量当中
public boolean isConnected(int p, int q);
朴素实现
假设存在编号分别为0~N-1的N个节点,那么在实现一个包含N个节点的并查集过程时。一个朴素的思想:我们可以通过一个数组进行维护。其中,数组的索引为节点编号,数组的值为该节点对应的连通分量标识。具体地,在union操作过程中,当两个节点的连通分量标识不一致时,需要遍历数组,将其中一个节点的连通分量标识全部修改为其中另外一个节点的连通分量标识。具体实现过程如下所示,可以看到这里直接将节点编号用来作为连通分量标识。不难看出该实现非常简单,虽然find操作非常快。但对于union操作而言,效率却不容乐观。因为其需要遍历整个数组
/**
* 并查集
* @author Aaron Zhu
* @date 2022-02-20
*/
public class UnionFind {
/**
* Key: 节点; Value: 节点对应的连通分量标识
*/
private int[] id;
/**
* 连通分量的数量
*/
private int count;
/**
* 构造并查集实例
* @param size 节点数量
*/
public UnionFind(int size) {
count = size;
id = new int[size];
for (int i=0; i id[i] = i;
}
}
/**
* 获取连通分量的数量
* @return
*/
public int getCount() {
return count;
}
/**
* 判断两个节点是否存在于同一个连通分量当中
* @param p
* @param q
* @return
*/
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 获取p节点所在连通分量的标识
* @param p
* @return
*/
public int find(int p) {
return id[p];
}
/**
* 建立p节点、q节点之间的连接
* @param p
* @param q
*/
public void union(int p, int q) {
int pId = find(p);
int qId = find(q);
if( pId == qId ) {
// p节点、q节点已经位于同一连通分量当中, 故直接返回
return;
}
// 将p节点所在连通分量的标识全部更改为q节点所在连通分量的标识
for(int i=0; i if( id[i] == pId ) {
id[i] = qId;
}
}
// 连通分量的数量减1
count--;
}
}
一种改进版本的并查集实现方案,即是提高优化union操作的时间效率。这时数组的值不再直接存储该节点对应的连通分量标识,而是存储当前节点所在连通分量的下一个节点。显然当数组的索引、值相同时,此时该索引对应的节点即是该连通分量的标识。事实上,这就是find操作的逻辑。而对于union操作而言,同样需要先通过find分别获取两个节点各自的根节点。如果不一致,则将其中一个节点的根节点指向另外一个节点的根节点即可。具体实现如下所示。不难看出在该实现下,Union操作效率得到了显著提高。一个连通分量中的各节点实际上构成了一种树形结构
/**
* Quick Union版本的并查集
* @author Aaron Zhu
* @date 2022-02-20
*/
public class QuickUnionUF {
/**
* Key: 节点; Value: 当前节点所在连通分量的下一个节点
*/
private int[] parent;
/**
* 连通分量的数量
*/
private int count;
/**
* 构造并查集实例
* @param size 节点数量
*/
public QuickUnionUF(int size) {
count = size;
parent = new int[size];
for (int i=0; i parent[i] = i;
}
}
/**
* 获取连通分量的数量
* @return
*/
public int getCount() {
return count;
}
/**
* 判断两个节点是否存在于同一个连通分量当中
* @param p
* @param q
* @return
*/
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 获取p节点所在连通分量的标识
* @param p
* @return
*/
public int find(int p) {
// 直到找到根节点
while (p != parent[p]) {
p = parent[p];
}
return parent[p];
}
/**
* 建立p节点、q节点之间的连接
* @param p
* @param q
*/
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if( pRoot==qRoot ) {
// p节点、q节点的根节点一样, 故直接返回
return;
}
// 将 p节点的根节点 指向 q节点的根节点
parent[pRoot] = qRoot;
// 连通分量的数量减1
count--;
}
}
优化
按秩合并
在Quick Union版本的并查集QuickUnionUF中,当进行union操作的两个节点并不是属于同一连通分量时。我们需要将其中一棵树的根节点指向另一颗树的根节点,以实现将两颗树合并为一棵树。但上述实现过程中,合并过程是随意的。可能是将大树的根节点指向小树的根节点,也可能是将小树的根节点指向大树的根节点。这里就引出另外一个问题了——何为大树?何为小树?理论上来说,按树的高度、树中节点的数量都可以作为树的比较标准。甚至从某种意义上来说,按树的高度可能更为贴切。但这样即会导致在同时使用路径压缩的场景时,树的实际高度也会发生变化。换言之这两种优化策略将会不完全兼容,树的高度实际上只是一个估计值了。故这里将树中节点的数量定义为秩Rank,将树中节点的数量作为树的比较标准。因为理论上来说,树越小、树中节点的数量越少,则树的高度自然也越小。而且其还能很好地与路径压缩优化策略进行兼容,因为一棵树无论怎么压缩路径,节点数都不会发生变化。至此,所谓按秩合并的策略就是在union操作过程中始终将 小树的根节点 指向 大树的根节点,以尽可能避免将二者合并为一颗高度更大的树

路径压缩
在Quick Union版本的并查集QuickUnionUF中,在不断进行union操作后。树的高度会越来越大,即使使用了按秩合并这一策略,也无法避免。所以一旦树中的节点距离根节点的路径过长,其显然会大大降低find操作的效率。为此我们需要在find操作中引入路径压缩这一优化策略,具体可分为:隔代路径压缩、完全路径压缩
「1. 隔代路径压缩」
所谓隔代路径压缩指的是在find操作过程中遍历某条路径时,不断将当前节点直接指向祖父节点(即父节点的父节点)。可以看到隔代路径压缩虽然压缩的不够彻底,但只需遍历一次效率较高
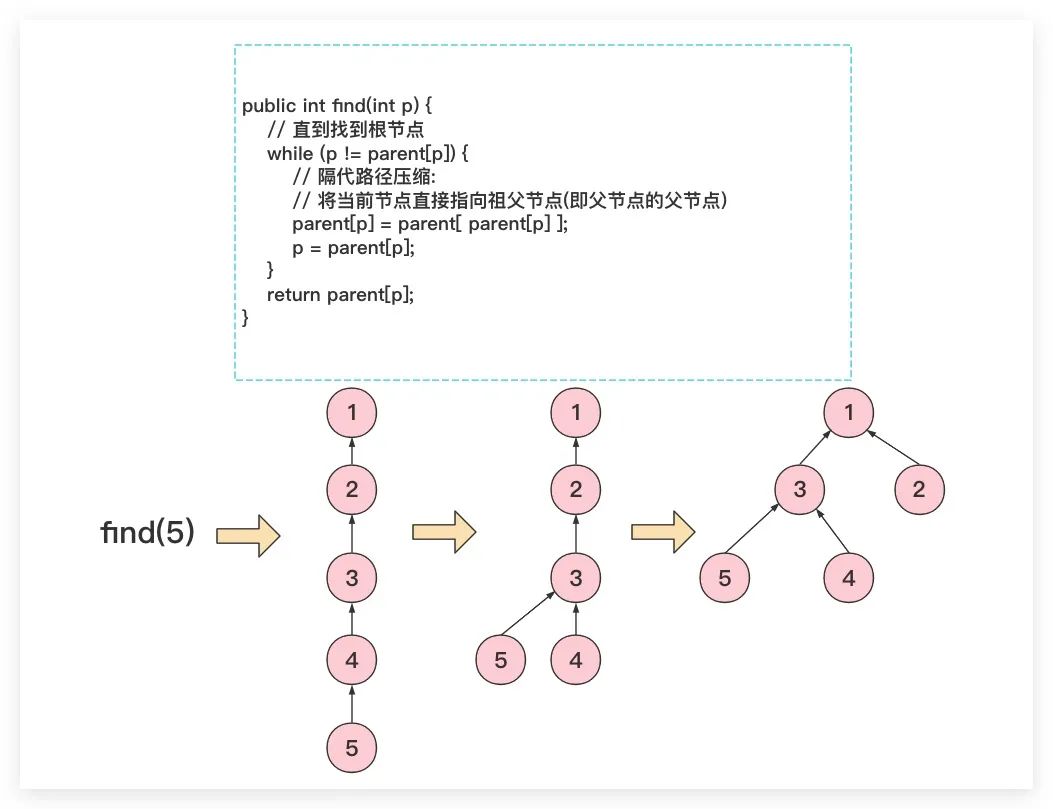
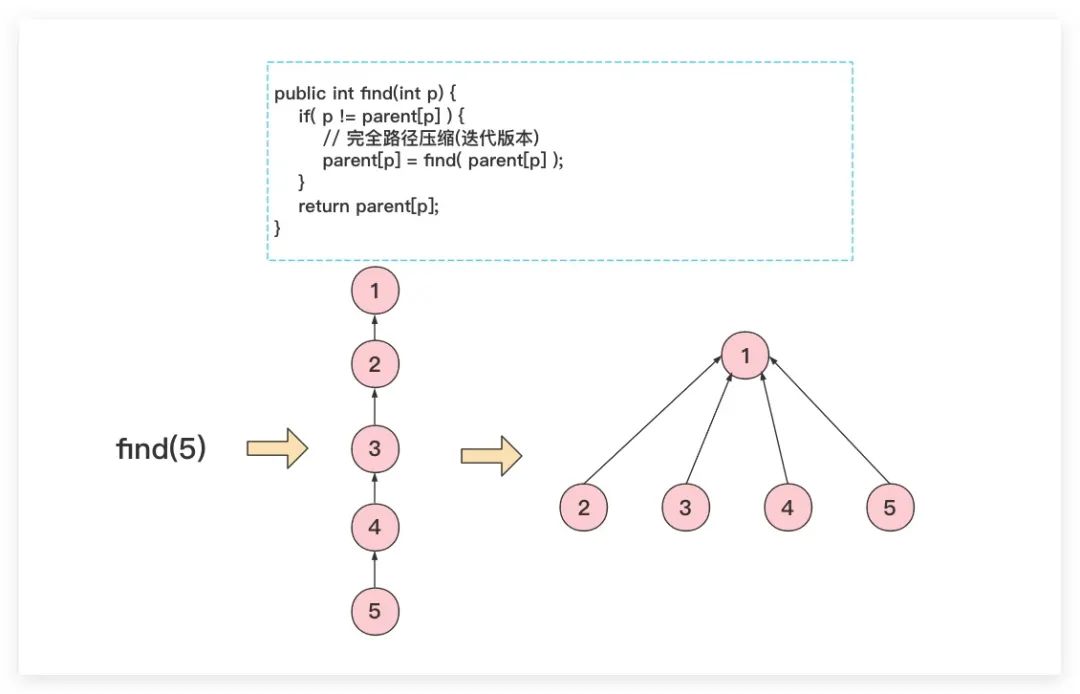
「2. 完全路径压缩」
如果期望将待查找节点到根节点到路径进行彻底压缩,即该条路径上点全部直连根节点。这就是所谓的完全路径压缩。而实现方式上较为简单的就是通过递归的方式进行实现;否则如果期望通过非递归的方式实现,则需要进行两次遍历。具体地:第一次遍历先找到根节点,第二次遍历则需将此条路径上的所有节点全部指向根节点
优化实现
这里我们将在朴素的Quick Union版本实现的基础上,对上述提到的两种优化思路进行实践落地、集中展示
package com.aaron.Algo;
/**
* 优化版本的并查集
* @author Aaron Zhu
* @date 2022-02-20
*/
public class UF2 {
/**
* Key: 节点; Value: 当前节点所在连通分量的下一个节点
*/
public int[] parent;
/**
* 根节点对应的秩, 即连通分量中的节点数
*/
private int[] rank;
/**
* 连通分量的数量
*/
private int count;
/**
* 构造并查集实例
* @param size 节点数量
*/
public UF2(int size) {
count = size;
parent = new int[size];
rank = new int[size];
for(int i=0; i parent[i] = i;
rank[i] = 1;
}
}
/**
* 获取连通分量的数量
* @return
*/
public int getCount() {
return count;
}
/**
* 判断两个节点是否存在于同一个连通分量当中
* @param p
* @param q
* @return
*/
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 获取p节点所在连通分量的标识
* @param p
* @return
* @apiNote 路径压缩: 隔代路径压缩
*/
public int find(int p) {
// 直到找到根节点
while (p != parent[p]) {
// 隔代路径压缩: 将当前节点直接指向祖父节点(即父节点的父节点)
parent[p] = parent[ parent[p] ];
p = parent[p];
}
return parent[p];
}
/**
* 获取p节点所在连通分量的标识
* @param p
* @return
* @apiNote 路径压缩: 完全路径压缩(迭代版本)
*/
/*
public int find(int p) {
if( p != parent[p] ) {
parent[p] = find( parent[p] );
}
return parent[p];
}
*/
/**
* 获取p节点所在连通分量的标识
* @param p
* @return
* @apiNote 路径压缩: 完全路径压缩(循环版本)
*/
/*
public int find(int p) {
// 1. 找到根节点Root
int root = p;
while(root!=parent[root]) {
root = parent[root];
}
// 2. 循环压缩 p->...->root 的路径
while( p != root ) {
// 暂存当前节点的下一个节点
int temp = parent[p];
// 将当前节点直接指向Root
parent[p] = root;
// 继续处理下一个节点
p = temp;
}
return root;
}
*/
/**
* 建立p节点、q节点之间的连接
* @param p
* @param q
*/
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if( pRoot==qRoot ) {
// p节点、q节点的根节点一样, 故直接返回
return;
}
// 将 小树的根节点 指向 大树的根节点
// 同时, 更新大树根节点对应的节点数
if(rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
rank[qRoot] += rank[pRoot];
} else {
parent[qRoot] = pRoot;
rank[pRoot] += rank[qRoot];
}
// 连通分量的数量减1
count--;
}
}
参考文献
算法·第4版 Robert Sedgewick、Kevin Wayne著
