用NumPy“弹奏”一首CD级音质的《爱的罗曼史》
Crossin的编程教室
共 30224字，需浏览 61分钟
· 2021-05-11
1 前言
pip install PyAudio
2 发出单一频率的声音
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 1158*np.pi, 66150, endpoint=False)
>>> y = np.sin(x) * 32767
>>> y.dtype
dtype('float64')
>>> y = y.astype(np.int16)
>>> y.dtype
dtype('int16')
>>> plt.plot(x, y, color='green')
>>> plt.show()
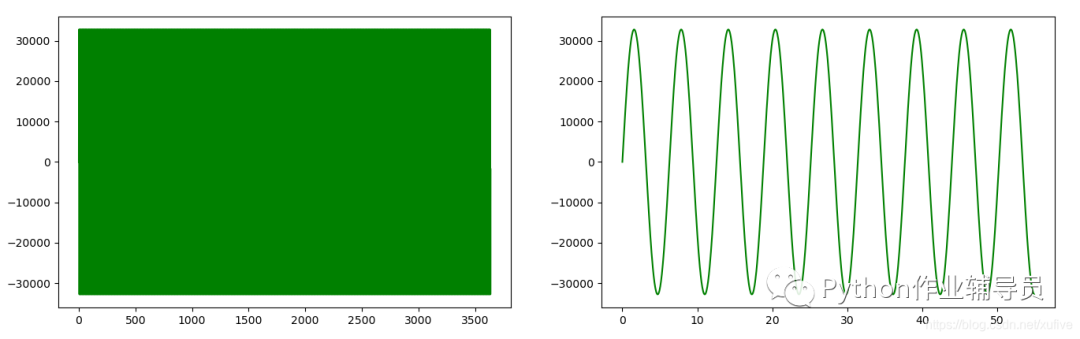
>>> import wave
>>> with wave.open(r'd:\sound_196Hz_3s.wav', 'wb') as fp:
fp.setparams((1, 2, 22050, 0, 'NONE', 'NONE'))
fp.writeframes(y.tobytes())
import pyaudio
import numpy as np
import time
def capture(rate, chunk):
pa = pyaudio.PyAudio()
stream = pa.open(
format = pyaudio.paInt16, # 设置量化精度（每个采样数据占用的位数）
channels = 1, # 设置单声道模式
rate = 22050, # 设置采样频率
frames_per_buffer = 2205, # 设置声卡读写缓冲区
input = True # 设置声卡输出模式
)
data = list()
while len(data) < 50:
data.append(np.frombuffer(stream.read(2205), dtype=np.int16))
stream.close()
pa.terminate()
return np.hstack(data)
if __name__ == '__main__':
for i in range(5):
print(5-i)
time.sleep(1)
print('Start')
data = capture(22050, 1024)
np.save('吉他10.npy', data)
import numpy as np
import matplotlib.pyplot as plt
import time
import wave
plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False
d1 = np.load('吉他10.npy')
d2 = np.load('吉他20.npy')
plt.subplot(221)
plt.plot(d1, c='g')
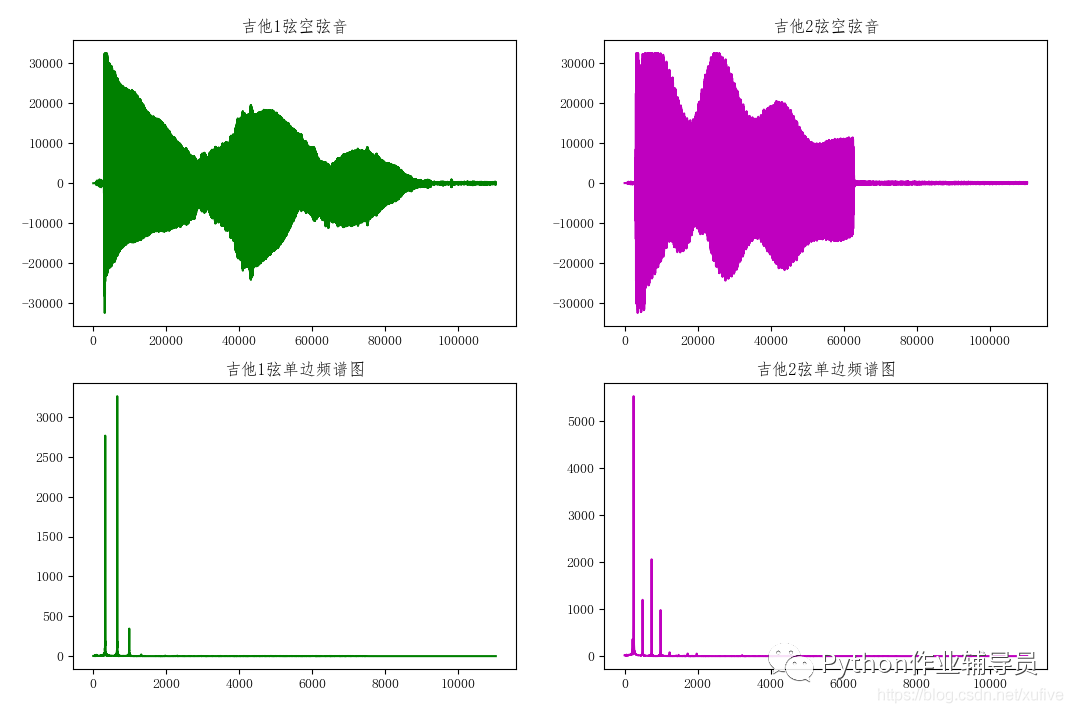
plt.title('吉他1弦空弦音')
plt.subplot(222)
plt.plot(d2, c='m')
plt.title('吉他2弦空弦音')
#plt.show()
fd1 = np.fft.fft(d1[22050:44100]) # 截取吉他1弦空弦音1秒钟的数据进行傅里叶分析
fd2 = np.fft.fft(d2[22050:44100]) # 截取吉他2弦空弦音1秒钟的数据进行傅里叶分析
plt.subplot(223)
plt.plot(np.abs(fd1[:11025]/22050), c='g')
plt.title('吉他1弦单边频谱图')
plt.subplot(224)
plt.plot(np.abs(fd2[:11025]/22050), c='m')
plt.title('吉他2弦单边频谱图')
plt.show()
声音幅度在振动中逐渐变小
频谱显示存在较强幅度的二倍频、三倍频、四倍频
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 3*np.pi, 22050, endpoint=False)
>>> y1 = 1-x/(10*np.pi)+(1-x/(6*np.pi))*np.sin(x)*0.5
>>> x = np.arange(3*22050)/22050
>>> y2 = 0.7*np.exp(-x)
>>> GUITAR_EFFECT_ARRAY = np.hstack((y1, y2))
>>> y_guitar = y*GUITAR_EFFECT_ARRAY[:y.shape[0]]
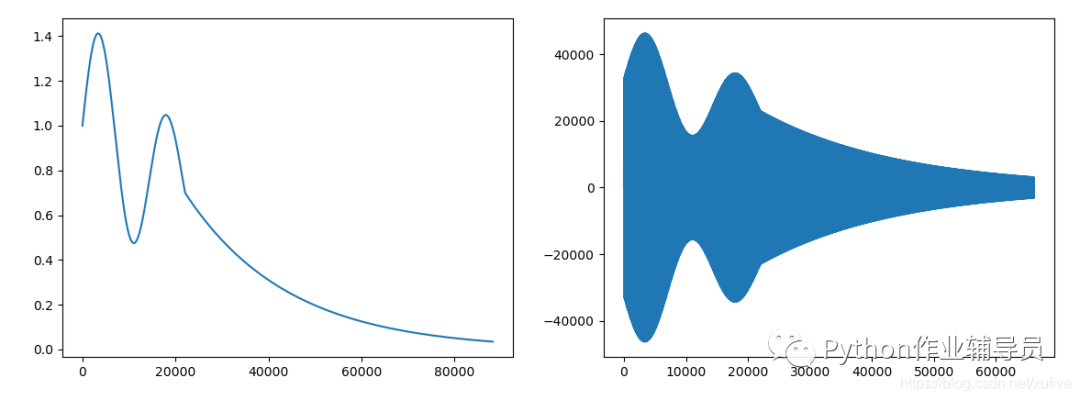
>>> plt.subplot(121)
>>> plt.plot(GUITAR_EFFECT_ARRAY)
>>> plt.subplot(122)
>>> plt.plot(y_guitar)
>>> plt.show()
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> plt.rcParams['font.sans-serif']=['FangSong']
>>> plt.rcParams['axes.unicode_minus']=False
>>> x1 = np.linspace(0, 4*np.pi, 300)
>>> x2 = np.linspace(0, 8*np.pi, 300)
>>> x3 = np.linspace(0, 12*np.pi, 300)
>>> y1 = np.sin(x1)
>>> y2 = np.sin(x2)
>>> y3 = np.sin(x3)
>>> y = np.sum(np.dstack((y1,y2,y3))[0], axis=1)
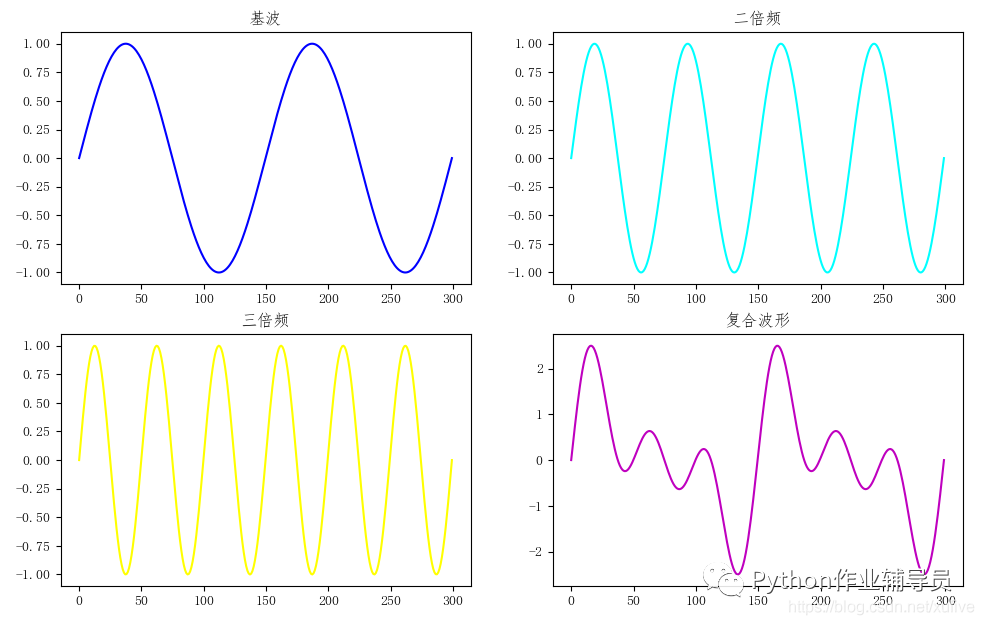
>>> plt.subplot(221)
>>> plt.title('基波')
>>> plt.plot(y1, c='be')
>>> plt.subplot(222)
>>> plt.title('二倍频')
>>> plt.plot(y2, c='cn')
>>> plt.subplot(223)
>>> plt.title('三倍频')
>>> plt.plot(y3, c='y')
>>> plt.subplot(224)
>>> plt.title('复合波形')
>>> plt.plot(y, c='m')
>>> plt.show()
def get_frequency(pos):
"""返回指定弦品pos的频率"""
fs = (329.6, 246.9, 196.0, 146.8, 110.0, 82.4)
if pos[0] == '0':
return 0
else:
return fs[int(pos[0])-1] * pow(2, int(pos[1:])/12)
5 吉他谱的格式约定
castle_in_the_sky= [
[ # 第1节
[('10',0.5),('12',0.5)] # 1弦
],
[ # 第2节
[('13',1.5),('12',0.5),('13',1),('13',0.5),('17',0.5)], # 1弦
[('0',1),('20',3)], # 2弦
[('0',0.5),('30',2),('30',1.5)], # 3弦
[('60',2),('60',2)] # 6弦
],
[ # 第3节
[('12',4)], # 1弦
[('0',1),('23',2),('20',1)], # 2弦
[('0',0.5),('32',1),('32',2.5)], # 3弦
[('40',2),('40',2)] # 4弦
],
[ # 第4节
[('10',2),('10',1),('13',1)], # 1弦
[('21',1.5),('23',2.5)], # 2弦
[('0',1),('30',1.5),('30',1),('30',0.5)], # 3弦
[('0',0.5),('42',3.5)], # 4弦
[('53',4)] # 5弦
],
[ # 第5节
[('23',3),('20',1)], # 2弦
[('0',1),('30',1),('30',2)], # 3弦
[('0',0.5),('40',1),('40',2.5)], # 4弦
[('52',4)] # 5弦
],
[ # 第6节
[('0',2.5),('13',1.5)], # 1弦
[('21',1.5),('20',0.5),('21',2)], # 2弦
[('0',1),('30',2.5),('30',0.5)], # 3弦
[('0',0.5),('42',2.5),('42',1)], # 4弦
[('50',2),('50',2)] # 5弦
],
[ # 第7节
[('0',3),('13',0.5),('13',0.5)], # 1弦
[('20',2),('20',2)], # 2弦
[('0',1),('30',3)], # 3弦
[('0',0.5),('42',1),('42',2.5)], # 4弦
[('60',4)] # 6弦
],
[ # 第8节
[('12',3),('12',0.5),('10',0.5)], # 1弦
[('0',1.5),('22',0.5),('22',2)], # 2弦
[('0',1),('33',1.5),('33',1.5)], # 3弦
[('0',0.5),('44',3.5)], # 4弦
[('62',2),('62',2)] # 6弦
],
[ # 第9节
[('12',2),('12',2)], # 1弦
[('0',1.5),('24',0.5),('24',2)], # 2弦
[('0',1),('34',1),('34',2)], # 3弦
[('0',0.5),('44',1.5),('44',2)], # 4弦
[('51',4)] # 5弦
]
]
6 弹奏吉他谱
import numpy as np
import wave
import pyaudio
SPEED = 80 # 用每分钟节拍数表示弹奏速度
FRAME_RATE = 44100 # 采样速率（44100为CD音质，22050为调频广播音质）
STEREO = True # 立体声（双声道）
# 生成吉他音色包络线
x = np.linspace(0, 3*np.pi, 2*int(FRAME_RATE*60/SPEED), endpoint=False)
y1 = 1 - x/(10*np.pi) + (1-x/(6*np.pi))*np.sin(x)*0.5
x = np.arange(6*int(FRAME_RATE*60/SPEED))/int(FRAME_RATE*60/SPEED)
y2 = 0.7*np.exp(-x)
GUITAR_EFFECT_ARRAY = np.hstack((y1, y2))
def get_frequency(pos):
"""返回指定弦品pos的频率"""
fs = (329.6, 246.9, 196.0, 146.8, 110.0, 82.4)
if pos[0] == '0':
return 0
else:
return fs[int(pos[0])-1] * pow(2, int(pos[1:])/12)
def get_wave(f, beat):
"""返回指定频率和节拍数的波形数据"""
data = list()
duration = beat*60/SPEED
sample_num = int(duration*FRAME_RATE)
for k, p in [(1,0.4), (2,0.3), (3,0.2), (4,0.1)]:
x = np.linspace(0, 2*duration*f*k*np.pi, sample_num, endpoint=False)
y = np.sin(x)*p
data.append(y)
return guitar_effect(np.sum(np.dstack(data)[0], axis=1))
def guitar_effect(data):
"""将等幅声波变成吉他音色的声波数据"""
return data*GUITAR_EFFECT_ARRAY[:data.shape[0]]
def play(melody, wave_file=None):
"""弹奏吉他谱，若wave_file存在，同时生成.wav文件"""
data = list()
for section in melody:
data_section = list()
for cord in section:
data_cord = list()
for pos, beat in cord:
f = get_frequency(pos)
dw = get_wave(f, beat)
data_cord.append(dw)
data_cord = np.hstack(data_cord)
data_section.append(data_cord)
d = data_section[0]
for i in range(1, len(data_section)):
if d.shape[0] > data_section[i].shape[0]:
d[:data_section[i].shape[0]] += data_section[i]
else:
data_section[i][:d.shape[0]] += d
d = data_section[i]
data.append(d)
data = np.hstack(data)
data = data*20000/data.max()
data = data.astype(np.int16)
if STEREO:
blank = np.zeros(int(0.006*FRAME_RATE), dtype=np.int16)
d_left = np.hstack((data, blank))
d_right = np.hstack((blank, data))
data = np.dstack((d_left, d_right))[0].ravel()
if wave_file:
with wave.open(wave_file, 'wb') as fp:
fp.setparams((int(STEREO)+1, 2, FRAME_RATE, 0, 'NONE', 'NONE'))
fp.writeframes(data.tobytes())
pa = pyaudio.PyAudio()
stream = pa.open(
format = pyaudio.paInt16, # 设置量化精度：每个采样数据占用的位数
channels = int(STEREO)+1, # 设置通道数量
rate = FRAME_RATE, # 设置采样频率
frames_per_buffer = 1024, # 设置声卡读写缓冲区
output = True # 设置声卡输出模式
)
for i in range(0, data.shape[0], 1024):
stream.write(data[i:i+1024].tobytes())
stream.stop_stream()
stream.close()
pa.terminate()
romance= [
[
[('17',1),('17',1),('17',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('17',1),('15',1),('13',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('13',1),('12',1),('10',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('10',1),('13',1),('17',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('112',1),('112',1),('112',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('112',1),('110',1),('18',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('18',1),('17',1),('15',1)],
[('0',0.33),('25',1),('25',1),('25',0.66)],
[('0',0.66),('35',1),('35',1),('35',0.33)],
[('50',3)]
],
[
[('15',1),('17',1),('18',1)],
[('0',0.33),('25',1),('25',1),('25',0.66)],
[('0',0.66),('35',1),('35',1),('35',0.33)],
[('50',3)]
],
[
[('17',1),('18',1),('17',1)],
[('0',0.33),('27',1),('27',1),('27',0.66)],
[('0',0.66),('38',1),('38',1),('38',0.33)],
[('67',3)]
],
[
[('111',1),('18',1),('17',1)],
[('0',0.33),('27',1),('27',1),('27',0.66)],
[('0',0.66),('38',1),('38',1),('38',0.33)],
[('67',3)]
],
[
[('17',1),('15',1),('13',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('13',1),('12',1),('10',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('60',3)]
],
[
[('12',1),('12',1),('12',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('32',1),('32',1),('32',0.33)],
[('52',3)]
],
[
[('12',1),('13',1),('12',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('32',1),('32',1),('32',0.33)],
[('52',3)]
],
[
[('10',1),('10',1),('10',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('30',1),('30',1),('30',0.33)],
[('42',1),('52',1),('63',1)]
],
[
[('10',3)],
[('20',3)],
[('30',3)],
[('60',3)]
],
[
[('14',1),('14',1),('14',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('31',1),('31',1),('31',0.33)],
[('60',3)]
],
[
[('14',1),('12',1),('10',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('31',1),('31',1),('31',0.33)],
[('60',3)]
],
[
[('25',1),('24',1),('24',1)],
[('0',0.33),('32',1),('32',1),('32',0.66)],
[('0',0.66),('44',1),('44',1),('44',0.33)],
[('50',3)]
],
[
[('24',1),('23',1),('24',1)],
[('0',0.33),('32',1),('32',1),('32',0.66)],
[('0',0.66),('44',1),('44',1),('44',0.33)],
[('50',3)]
],
[
[('19',1),('19',1),('19',1)],
[('0',0.33),('27',1),('27',1),('27',0.66)],
[('0',0.66),('38',1),('38',1),('38',0.33)],
[('67',3)]
],
[
[('19',1),('111',1),('19',1)],
[('0',0.33),('27',1),('27',1),('27',0.66)],
[('0',0.66),('38',1),('38',1),('38',0.33)],
[('67',3)]
],
[
[('19',1),('17',1),('17',1)],
[('0',0.33),('29',1),('29',1),('29',0.66)],
[('0',0.66),('39',1),('39',1),('39',0.33)],
[('60',3)]
],
[
[('17',1),('19',1),('111',1)],
[('0',0.33),('29',1),('29',1),('29',0.66)],
[('0',0.66),('39',1),('39',1),('39',0.33)],
[('60',3)]
],
[
[('112',1),('112',1),('112',1)],
[('0',0.33),('29',1),('29',1),('29',0.66)],
[('0',0.66),('39',1),('39',1),('39',0.33)],
[('60',3)]
],
[
[('112',1),('111',1),('110',1)],
[('0',0.33),('29',1),('29',1),('29',0.66)],
[('0',0.66),('39',1),('39',1),('39',0.33)],
[('60',3)]
],
[
[('19',1),('19',1),('19',1)],
[('0',0.33),('25',1),('25',1),('25',0.66)],
[('0',0.66),('36',1),('36',1),('36',0.33)],
[('50',3)]
],
[
[('19',1),('17',1),('15',1)],
[('0',0.33),('25',1),('25',1),('25',0.66)],
[('0',0.66),('36',1),('36',1),('36',0.33)],
[('50',3)]
],
[
[('14',1),('14',1),('14',1)],
[('0',0.33),('24',1),('24',1),('24',0.66)],
[('0',0.66),('32',1),('32',1),('32',0.33)],
[('52',3)]
],
[
[('14',1),('15',1),('12',1)],
[('0',0.33),('24',1),('24',1),('24',0.66)],
[('0',0.66),('32',1),('32',1),('32',0.33)],
[('52',3)]
],
[
[('10',1),('10',1),('10',1)],
[('0',0.33),('20',1),('20',1),('20',0.66)],
[('0',0.66),('31',1),('31',1),('31',0.33)],
[('42',1),('52',1),('64',1)]
],
[
[('10',3)],
[('20',3)],
[('30',3)],
[('60',3)]
]
]
play(romance)
play(romance, '爱的罗曼史.wav')
还不错吧？
完整代码都在文中了，感兴趣的同学可以自己复制到代码中试一下，也可以改成你喜欢的曲目。
如果文章对你有帮助，欢迎转发/点赞/收藏~
作者：天元浪子
_往期文章推荐_
评论
真高！比亚迪员工爆料比亚迪在越南的薪资水平：基本工资480万，全勤奖35万，交通补助20万，餐补110万，每周6天，每天10小时
上一篇：某大公司为逼迫员工离职，竟然把他的工位安排到厕所旁，没想到他直接开始记录领导的如厕时间，还发到公司大群...对此，你怎么看？--完--PS：欢迎在留言区留下你的观点，一起讨论提高。如果今天的文章让你有新的启发，欢迎转发分享给更多人。全文完，感谢你的耐心阅读。如果你还想看到我的文章，请一定给本
开发者全社区
0
太敢穿了！透视纱裙！性感火辣的身材
绝了呀今天的厂花：吴宣仪1995年1月26日，吴宣仪出生于海南省海口市，中国内地流行乐女歌手、影视演员。2016年2月，吴宣仪随宇宙少女发行首张迷你专辑正式出道。2018年4月，她参加《创造101》综艺选秀，获得第二名，成功加入火箭少女101组合。吴宣仪的颜值一直备受称赞，她的五官立体精致，皮肤白皙
逆锋起笔
0
某大公司为逼迫员工离职，竟然把他的工位安排到厕所旁，没想到他直接开始记录领导的如厕时间，还发到公司大群...
上一篇：字节的跳动职级与薪资（2024年）我们与公司间的合作，宛如两艘船只在茫茫大海上相互依靠，共同抵御风浪，携手驶向成功的彼岸。然而，当航向开始产生分歧，或是波涛汹涌的风浪改变了我们的初衷，我们或许应当冷静地选择和平分手，而非在风雨中硬撑。最近，一位网友的遭遇引起了广大职场人的关注和热议。这位网友
开发者全社区
0
金融研究 | 使用Python测量关键审计事项的「信息含量」
Tips: 公众号推送后内容只能更改一次，且只能改20字符。如果内容出问题，或者想更新内容， 只能重复推送。为了更好的阅读体验，建议阅读本文博客版， 链接地址https://textdata.cn/blog/2023-01-13-information-content-of-critical-aud
大邓和他的Python
0
我看阿里的年终奖总算发了！
到4月底了，这两天看朋友圈，发现阿里的年终奖终于发了，问了问老同学，也从网上检索了不少信息，基本搞清楚了阿里今年的年终奖情况。近来来阿里一些集团对绩效等级做了较大的调整，以前的旧绩效系统中，绩效分为3.25、3.5、3.75、4和5五个等级，其中4和5是较高绩效等级，较少见。而且之前3.5绩效内部划
公子龙
0
CVPR 2024｜大视觉模型的开山之作！无需任何语言数据即可打造大视觉模型
↑ 点击蓝字 关注极市平台作者丨科技猛兽编辑丨极市平台极市导读 本文提出一种序列建模 (sequential modeling) 的方法，不使用任何语言数据，训练大视觉模型。>>加入极市CV技术交流群，走在计算机视觉的最前沿本文目录1 序列建模打造大视觉模型(来自 U
极市平台
1
金融研究(更新) | 使用Python构建关键审计事项的「信息含量」
Tips: 公众号推送后内容只能更改一次，且只能改20字符。如果内容出问题，或者想更新内容， 只能重复推送。为了更好的阅读体验，建议阅读本文博客版， 链接地址https://textdata.cn/blog/2023-01-13-information-content-of-critical-aud
大邓和他的Python
0
字节的跳动职级与薪资（2024年）
上一篇：阿里公布年终奖，P7, 3.5+，22W年终奖，还有35W长期现金激励，真香字节跳动自2012年3月成立以来，已经迅速成长为一个全球性的科技公司。其产品和服务已经遍布全球150多个国家与地区，并且支持超过75种不同的语言。在字节跳动的官方网站上，列出了一系列引人注目的产品和服务，包括但不限于
开发者全社区
0