使用 NumPy 的标准化技巧-技术圈

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

数据科学不仅仅是开发模型，也有很多像清洗数据和选择有效特征的工作。将特征插入到一个具有相似的分布但是方式明显不同的模型中，或者是在极不相同的尺度上，可能会导致错误的预测。解决这些问题的通用方法是首先使用“标准化”特征来消除均值和方差的显著差异。

术语“标准化”可能会产生误导(也不应该与数据库规范化混淆) ，因为它在统计学中有很多含义。然而，在标准化技术中有一个共同的主题，那就是将单独的数据集对齐以便于比较。我们将关注的两个技术是提取残差，它改变了数据集的均值，以及重新缩放数据集中的值从0到1的尺度。

提取平均差

让我们首先探索提取平均差技术。平均差是数据集中的值与数据集的平均值之间的相对差异。当数据集具有相似的分布但是方法明显不同，从而使得数据集之间的比较变得困难时，这种技术非常有用。例如，假设我们有一个同等规模的两个不同班级参加的考试。问题是一样的，顺序是一样的，答案也是一样的。然而，这两个班级的平均分数是不同的。一班的平均成绩是82分，二班的平均成绩是77分。我们怎样才能把这两个班的成绩合并起来呢？

让我们从设置 Python 环境开始：

import numpy as npimport scipy.stats as stfrom sci_analysis import analyze%matplotlib inlinenp.random.seed(12)

上面的代码导入 NumPy 包 as np，导入 scipy.stats as st 用于创建我们的数据集，sci_analysis 中的 analyze 函数可以用来绘图最终结果，最后，我们设置随机数生成器的种子值以使结果可重复。作为参数传递给 np.random.seed()的数字12是任意选择的。现在，让我们为每个类创建两个数据集：

dist1 = st.norm.rvs(82, 4, size=25).astype(int)dist2 = st.norm.rvs(77, 7, size=25).astype(int)print(dist1)print(dist2)

输出：

[83 79 82 75 85 75 82 81 78 93 79 83 86 77 87 81 86 78 77 86 84 82 84 84 77][61 65 64 61 72 73 76 78 74 75 77 70 72 77 72 72 76 86 79 74 72 76 92 54 80]

类1用 dist1表示，类2用 dist2表示。这两个变量都是 NumPy 数组，由25个正态分布的随机变量组成，dist1的平均值为82，标准差为4，dist2的平均值为77，标准差为7。两个数组都被转换为整数数据类型，以完成我们的考试成绩示例。我们可以通过下面的代码直观地看到这个课程的分数：

analyze(    {'dist1': dist1, 'dist2': dist2},    title='Different means',    nqp=False,)print(f'dist1 mean: {np.mean(dist1)} std dev: {np.std(dist1)}')print(f'dist2 mean: {np.mean(dist2)} std dev: {np.std(dist2)}')

输出：

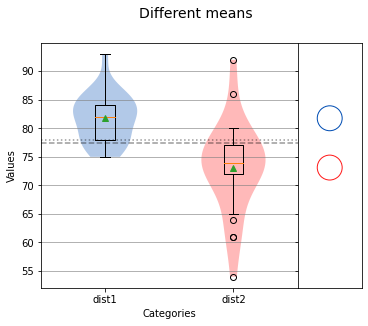
dist1 mean: 81.76 std dev: 4.197904239022134dist2 mean: 73.12 std dev: 7.7785345663563135

从上面的图以及 dist1和 dist2的均值和标准差，我们可以判断这些分布是不匹配的。

现在我们来计算 dist1和 dist2的平均差：

dist1_norm = dist1 - int(np.mean(dist1))dist2_norm = dist2 - int(np.mean(dist2))print(dist1_norm)print(dist2_norm)

输出：

[   2  -2   1  -6   4   -6   1   0  -3  12   -2   2   5  -4   6    0   5  -3  -4   5    3   1   3   3  -4][ -12  -8  -9 -12  -1    0   3   5   1   2    4  -3  -1   4  -1   -1   3  13   6   1     -1   3  19 -19   7]

平均差是每个值与平均值之间的差值。换句话说，每个平均差是到每个分布的平均值（此时为0）的距离。由于每个分布现在都有一个平均值为零，它们现在可以直接相互比较。

analyze(    {'dist1': dist1_norm, 'dist2': dist2_norm},    title='Normalized',    nqp=False,)print(f'dist1 mean: {np.mean(dist1_norm)} std dev: {np.std(dist1_norm)}')print(f'dist2 mean: {np.mean(dist2_norm)} std dev: {np.std(dist2_norm)}')

输出：

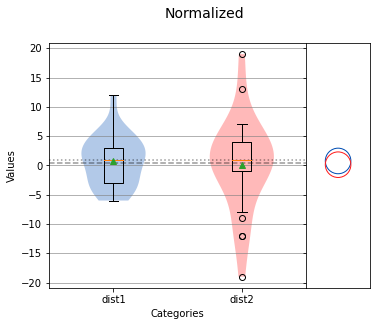
dist1 mean: 0.76 std dev: 4.197904239022134dist2 mean: 0.12 std dev: 7.7785345663563135

我们可以看到，平均值现在接近于零(如果将值转换为整数时没有舍入误差，平均值将为零) ，但是每个分布的方差并没有改变。这表明计算平均差是如何有效地改变每个分布的均值，以便对齐它们进行直接比较。

Min-Max Re-scaling

另一种标准化技术是重新缩放数据集。当试图比较不同因素的数据集或使用不同单位的数据集时，比如比较英里数和米数时，这是非常有用的。让我们生成两个不同尺度（相差大概100倍）的数据：

dist3 = st.gamma.rvs(1.7, size=25)dist4 = st.gamma.rvs(120, size=25)print(dist3)print(dist4)

输出：

[   0.49529541   1.42598239   0.38621773   0.96738928   0.53575876    1.72574991   0.3431045    0.80584646   0.77543188   1.84272915    2.049985     0.76373308   3.54020309   0.36979422   4.67967817    0.6311116    2.51371776   1.12812921   0.62183125   2.03923847    1.15269735   0.72795499   1.86093872   0.52560778   0.65314453] [113.88768554 108.94661696 118.40872068 124.94416222 150.91953839  116.86987547 107.05486021  89.61392457 126.28254195 123.32858014  108.31036684 114.52812809 109.43092709 114.17768634 114.54545154  111.21616394 102.08437696 127.42455395 105.82224292 127.28966453  114.03632754 120.02256655 120.77792085 103.43640076 112.24143473]

从上面的输出中，你可以看到 dist3在0到10之间，dist4比 dist3大100倍。通过检查平均值和标准差，我们可以看出这些分布是无法相互比较的。

analyze(    {"dist3": dist3, "dist4": dist4},    title="Different Scales",    nqp=False,)print(f'dist3 mean: {np.mean(dist3)} std dev: {np.std(dist3)}')print(f'dist4 mean: {np.mean(dist4)} std dev: {np.std(dist4)}')

输出：

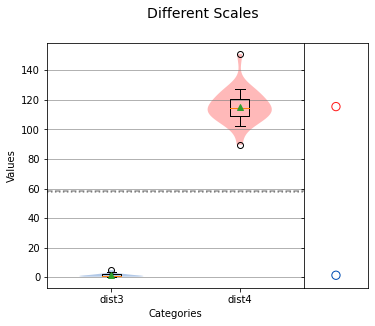
dist3 mean: 1.3024508282047844 std dev: 1.0372657584518052dist4 mean: 115.42402875045401 std dev: 11.29662689178773

幸运的是，我们可以通过每个数据集中的值和最小值的差值到最大值和最小值的差值的比值对数据进行处理。用公式表示如下：

(x - min) / (max - min)

通过在 Python 中应用这个方程，我们可以得到 dist3和 dist4的处理后的结果：

max = np.max(dist3)min = np.min(dist3)dist3_scaled = np.array([(x - min) / (max - min) for x in dist3])max = np.max(dist4)min = np.min(dist4)dist4_scaled = np.array([(x - min) / (max - min) for x in dist4])print(dist3_scaled)print(dist4_scaled)

输出：

[0.03509474 0.24970817 0.00994177 0.14395807 0.04442546 0.3188336  0.         0.10670681 0.09969331 0.34580864 0.39360118 0.09699561 0.7372407  0.00615456 1.         0.06641352 0.50053647 0.18102418 0.0642735  0.39112306 0.18668952 0.08874529 0.35000771 0.04208467 0.07149424] [0.39594679 0.31534946 0.46969265 0.57629694 1.         0.44459144 0.28449166 0.         0.59812822 0.54994402 0.30497113 0.40639351 0.32324939 0.4006772  0.40667608 0.35236968 0.20341453 0.6167564  0.26438555 0.61455612 0.3983714  0.49601725 0.50833838 0.22546836 0.36909361]

通过重新缩放 dist3和 dist4，每个数据集的最大值现在是1，而最小值现在是0。这很方便，因为现在每个数据集都在同一尺度上，并且每个分布的形状都保留了下来。实际上，每个分布都被压缩并移动到0到1之间。现在，让我们检查一下重新缩放的 dist3和 dist4的平均标准差：

analyze(    {'dist3': dist3_scaled, 'dist4': dist4_scaled},    title='Scaled',    nqp=False,)print(f'dist3 mean: {np.mean(dist3_scaled)} std dev: {np.std(dist3_scaled)}')print(f'dist4 mean: {np.mean(dist4_scaled)} std dev:{np.std(dist4_scaled)}')

输出：

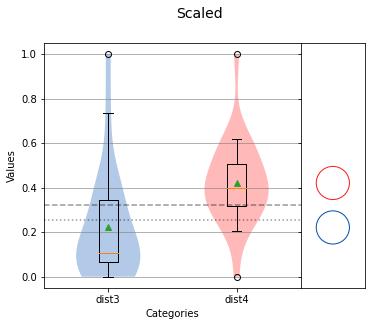
dist3 mean: 0.2212221913870349 std dev: 0.2391901615794912dist4 mean: 0.42100718959757816 std dev: 0.18426741349056594

我们现在可以看到，对于dist3_scaled和dist4_scaled，在相似的标准偏差下，两者有着显著的不同。

使用 NumPy 标准化大数据集

平均差和重新缩放都是用于分析的数据集标准化的有用技术。然而，这些数据集通常不止25个值，因此值得考虑如何计算平均差并有效地执行重新缩放。值得庆幸的是，NumPy 可以帮助快速有效地执行这些计算。

NumPy 是一个用于高性能科学计算的 Python 包。与使用常规 Python 列表相比，NumPy 有两个特性可以使计算更快、更高效。首先，NumPy 使用数组作为其主数据结构，与 Python 列表相比，它使用的内存更少，并且要求数组中的每个值都是相同的类型。数组也可以由标量操作ーー对数组的每个值应用标量操作。实际上，我们在通过从分布(数组)中减去分布(标量)的平均值来计算平均差时已经看到了这一点。

让我们比较一下使用 Python 列表解析和数组操作计算平均差的速度差异。首先，我们创建一个随机的、正态分布的变量数组，其值为100,000：

dist5 = st.norm.rvs(82, 5, size=100000)

让我们看看使用列表解析计算 dist5的平均差需要多长时间：

avg = np.mean(dist5)%timeit [val - avg for val in dist5]

输出：

10 loops, best of 3: 24.9 ms per loop

在 dist5中迭代每个值大约需要25毫秒，这个列表解析还不错。然而，让我们再次计算 dist5的平均差，但是使用 NumPy 标量操作：

avg = np.mean(dist5)%timeit dist5 - avg

输出：

10000 loops, best of 3: 144 µs per loop

仅仅从 dist5(NumPy 数组)减去平均值就需要144ms！这要感谢 NumPy 数组的高效设计。

现在，如果我们想要操作一个带有函数的数组，而不仅仅是一个简单的标量，那么该怎么办呢？这是 NumPy 第二次以通用函数的形式提高 Python 的性能。通用函数是“向量化”操作，它利用 CPU 优化来实现迭代数组中的每个值时的计算速度加快。NumPy 有许多内置的通用函数，但我们也可以使用 NumPy 的 frompyfunc()函数编写自己的函数。

让我们来看看使用列表解析和自定义通用函数重新缩放数组值的速度差异：

min = np.min(dist5)max = np.max(dist5)%timeit [(val - min) / (max - min) for val in dist5]

输出：

10 loops, best of 3: 47.2 ms per loop

列表内涵对dist5进行re-scale操作仅使用了47ms，可以实现令人钦佩的性能。让我们将其与创建一个称为 scale 的自定义通用函数相比较。

scale = np.frompyfunc(lambda x, min, max: (x - min) / (max - min), 3, 1)

我们将使用 np.frompyfunc()函数，它接受一个可调用的、输入的数量和输出的数量作为参数。在这种情况下，可调用的是以 lambda 函数形式出现的重定标方程。如果您不熟悉 lambda 函数，可以将它们看作一行未命名的函数。我们的 lambda 函数有三个参数: x、 min 和 max。这三个参数是在调用 np.frompyfunc()时指定的三个输入。同样值得注意的是，min 和 max 是由 dist5计算的标量，而 x 表示 dist5中的每个值。现在，让我们计算 min 和 max 并调用 scale 函数：

min = np.min(dist5)max = np.max(dist5)%timeit scale(dist5, min, max).astype(float)

输出：

10 loops, best of 3: 20.4 ms per loop

正如你所看到的，自定义通用函数与列表解析相比只需要一半的时间就可以完成。

总结

我们研究了两种归一化技术：提取平均差和最小最大值重新缩放。提取平均差可以被认为是一个分布的转移，所以它的平均值是0。最小-最大值重新缩放可以被认为是移动和压缩数据集的分布，以便取值归一化值0和1之间。平均差提取可用于比较不同方法但具有相似分布的情况。最小-最大值重新缩放是比较不同尺度和不同形状分布的有用方法。

当分布被表示为 NumPy 数组时，这两种规范化技术都可以通过 NumPy 有效地执行。NumPy 数组上的标量操作快速且易于读取。当需要对数组进行更复杂的操作时，可以使用通用函数高效地执行操作。

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目31讲

在「小白学视觉」公众号后台回复：Python视觉实战项目31讲，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲

在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

下载4：leetcode算法开源书

在「小白学视觉」公众号后台回复：leetcode，即可下载。每题都 runtime beats 100% 的开源好书，你值得拥有！

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~