点击上方“程序员大白”，选择“星标”公众号

重磅干货，第一时间送达

跳表(SkipList)

简介

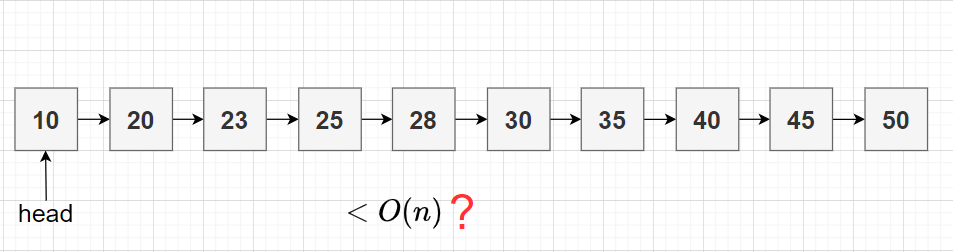
首先，我们在心里思考一个问题：排序单链表的查找时间复杂度能否比好呢？

对于一个已经排好序的单链表来说，想要查询其中的一个数据，也只能从头开始遍历链表，不能跳过节点（skip nodes）查找，这样效率很低，时间复杂度为。

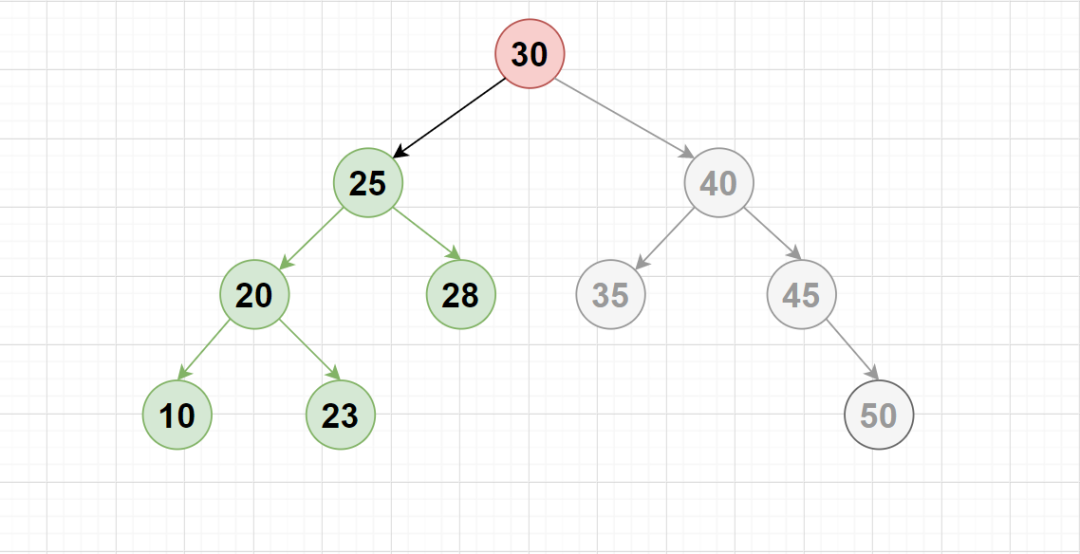
如上图所示，对于平衡二叉搜索树（AVL 树），在与根进行一次比较后，我们跳过了几乎一半的节点。

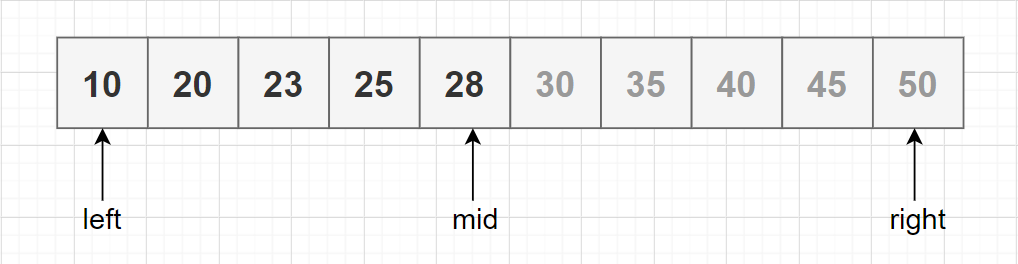
对于排序的数组，我们可以随机访问，并且可以对数组应用二分查找法。

那我们是不是可以对排序单链表进行增强（比如像二分查找一样）来提高查找速度呢？那就是 跳表（Skip List）。

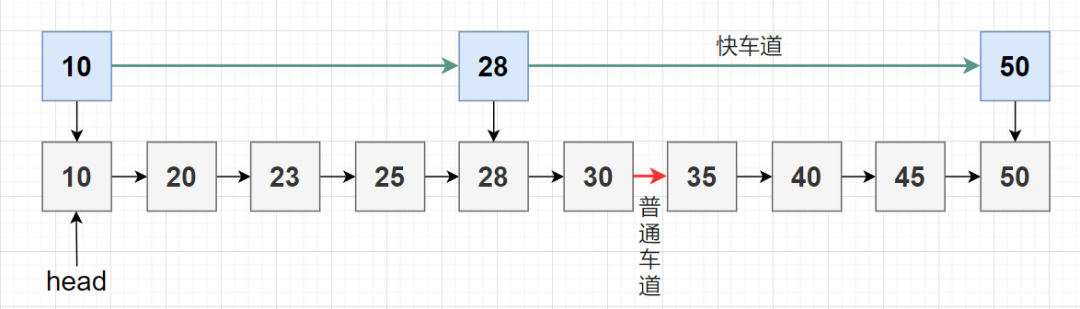
这个想法很简单，我们通过创建多层链表，这样我们就可以跳过一些节点。

如上图中例子，其中包含 10个节点和两层。上层是只连接主要车站的 “快车道”，下层是连接每个车站的 “普通车道”。就像你从北京出发，自驾到西藏，如果你走 “国道”，你可能要路过很多站点，速度也会比较慢；但是也有直达的 “高速公路” 呀（京藏高速），高速公路上的出站口少，但是你到达目的地更快呀。

假设我们要查找 35，我们从“快车道” 的第一个节点开始，一直沿着“快车道”前进，直到找到下一个节点大于 35 的节点。一旦我们在“快速车道”上找到这样的节点( 28 就是我们找到的节点，28 的下一个节点 50 大于 35)，我们就使用节点 28 的指针移动到 “普通车道” ，并在 “普通车道” 上线性查找 35 。在图中的例子中，我们从“普通车道”上的 28 开始，通过线性搜索，我们找到了 35。

原本需要 6 次才能查找到元素 35 ，现在仅查找了 4 次。

那么图中的两层情况下的时间复杂度是多少？

最坏情况下的时间复杂度是“快车道”上的节点数加上“普通车道”上的一个段（段表示两个“快车道”节点之间的“普通车道”节点的数目）的节点数。

因此，如果我们在“正常车道”上有 n 个节点，在“快速车道”上有节点，并且我们将 “普通车道” 均分，那么在 “普通车道” 的每一段中都有个节点。实际上是具有两层跳表结构的最优除法。通过这种规则，搜索遍历链表节点将为。因此，在增加空间的情况下，可以将时间复杂度降低到。

那么我们能将时间复杂度降得更低吗？

通过增加更多的层可以进一步降低跳表的时间复杂度。实际上，在个额外空间的情况下，查找、插入和删除的期望时间复杂度都可以达到。

跳表的插入操作

在深入理解跳表的插入操作之前，一定要解决跳表的层数问题！！！

层数的确定

链表中的每个元素都由一个节点表示，节点的层级是在插入链表时随机选择的。跳表中节点的层级不取决于节点中的元素数量，而是由下面一个算法确定的，算法的 Java 代码为：

private int randomLevel() {
 int level = 1; 
    while (Math.random() < P && level < MaxLevel {
        level++;
    }
    return level;
}

MaxLevel 是跳表层数的上限。它可以确定为，是中的节点总数。上述算法保证了随机层数永远不会大于 MaxLevel 。这里 P 是第 i+1 层节点的个数与第 i 层节点个数的比值，比如，就表示第 i 层的节点个数是第 i+1 层节点个数的两倍，理论情况下如下图所示，跳表可以和 AVL 树达到几乎一样的效果：

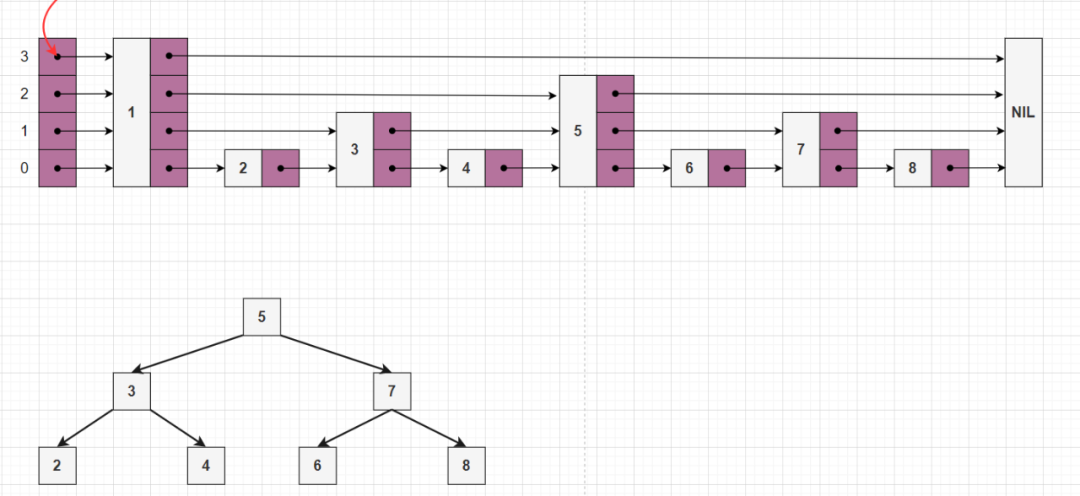
理论来讲，对于，一级索引中元素个数应该占原始数据的 50% （原始数据 8 个，第一层索引 4 个），二级索引中元素个数占原始的 25%，三级索引占原始数据的 12.5% ，一直到最顶层。

对于每一个新插入的节点，都需要调用 randomLevel() 生成一个合理的层数。该randomLevel() 方法会随机生成 1 ~ MaxLevel 之间的数，且：的概率返回 1，的概率返回 2，的概率返回 3 ...

节点结构

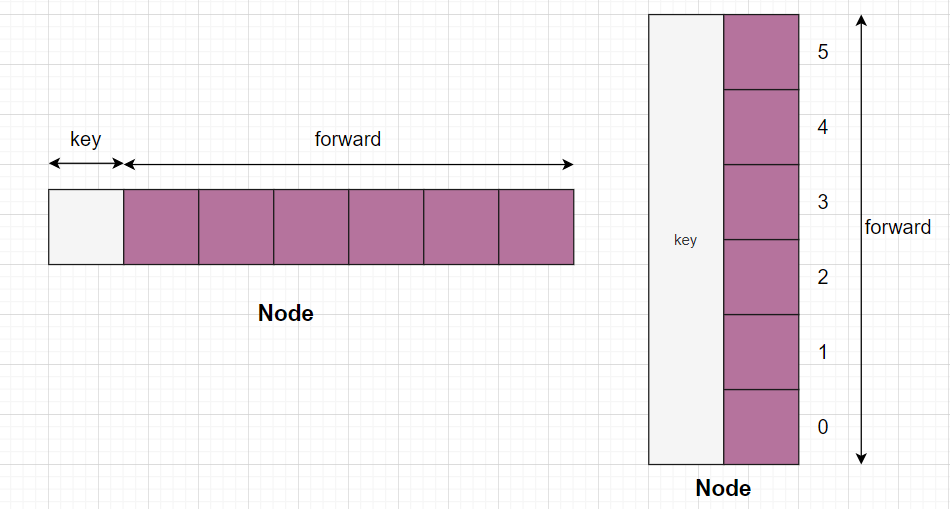
每个节点由一个关键字 key 和一个前向数组 forwards[] 组成，该数组存储指向不同层的节点的指针。i 层的节点的前向数组保存了从第 0 层到第 i 层前向节点的指针。

public class Node {
        private int key = -1; //结点的 key 
        private Node forwards[] = new Node[MAX_LEVEL];  // 结点key 所对应的前向数组
}

插入操作

我们将从列表的最高层开始，将当前节点的下一个节点的 key 与要插入的 key 进行比较。基本思想是：

如果下一个节点的 key 小于要插入的 key ，则我们在同一层上继续前进查找。
如果下一个节点的 key 大于要插入的 key ，则我们将指向当前节点 i 的指针存储在 update[i] 处，并向下移动一层，继续搜索。

在第 0 层，我们一定会找到一个位置来插入给定的 key 。

以下是插入操作的伪代码：

public void insert(int key) {
    int level = randomLevel();
    Node newNode = new Node();
    newNode.key = key;
    newNode.maxLevel = level;
    // 创建 update 数组并初始化
    Node update[] = new Node[level];
    for (int i = 0; i < level; ++i) {
        update[i] = head;
    }
    // 将查找路径上结点的前向结点设置为新插入结点
    Node current = head;
    for (int i = level - 1; i >= 0; --i) {
        while (current.forwards[i] != null && current.forwards[i].key < key) {
            current = current.forwards[i];
        }
        update[i] = current;// 第 i 层需要修改的节点为 p
    }
    current = current.forwards[0];
    if (current == null || current.key != key) {
        // 在第0到level层插入新结点
        for (int i = 0; i < level; ++i) {
            newNode.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = newNode;
        }
    }
    // 更新跳表的层数
    if (currentLevel < level) currentLevel = level;
}

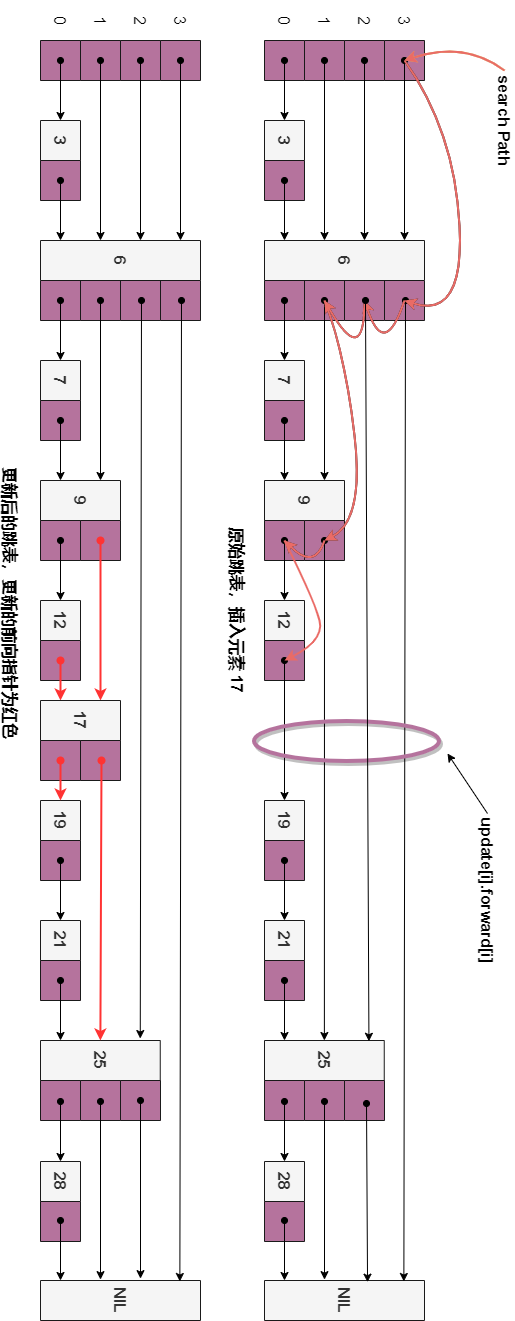
在这里，update[i] 表示插入值为 key 的节点时，第 i 层需要修改的节点为 p，也就是位于查找路径上的节点。考虑以下示例，我们想要在其中插入值 17，设随机层数为 randomLevel() == 2 ，update[] 函数就包含两个元素，update[1] 存储的是 key 为 9 的结点的地址，update[0] 存储的是值为 12 的结点的地址，当插入值 17 之后，9 和 12 的前向结点就变成了 17 ，而 17 的前向结点就变成了**9** 和 12 原始的前向结 25 和 19 。

跳表的查找操作

跳表的查找操纵非常类似于在跳表插入操作中搜索插入元素的位置的方法。基本的想法是：

下一个节点的关键字 key 小于查找的关键字，则我们在同一层上继续前进查找。
下一个节点的关键字 key 大于查找的关键字，则我们将指向当前节点i的指针存储在 update[i] 处，并向下移动一层，继续搜索。

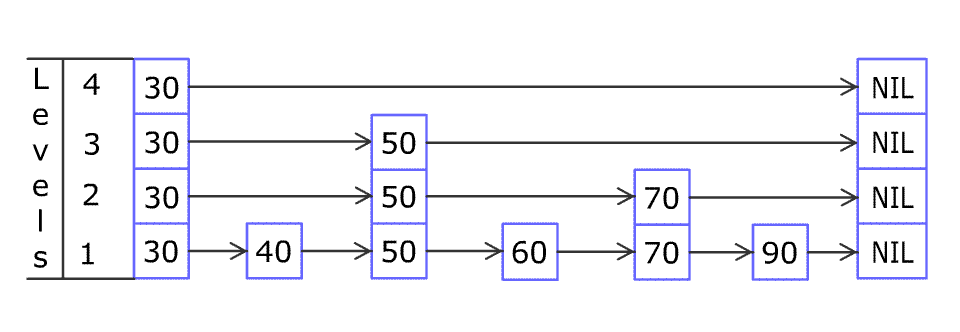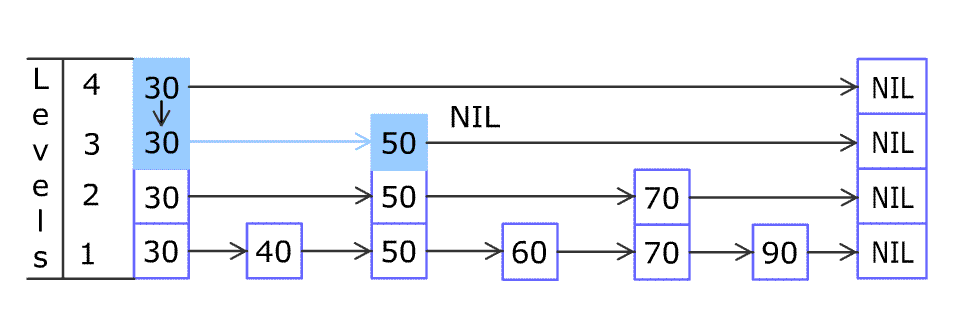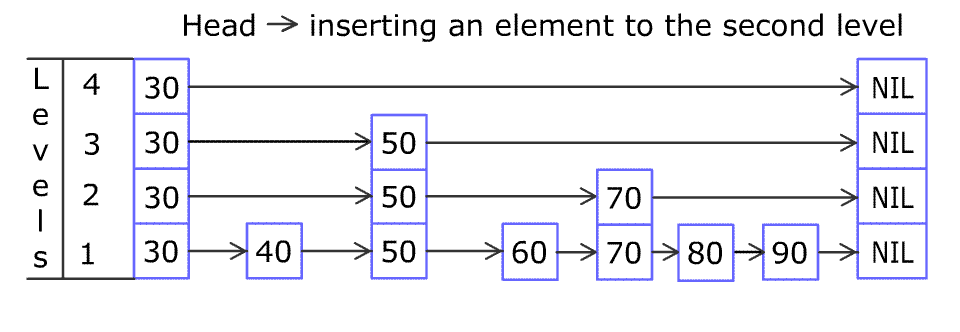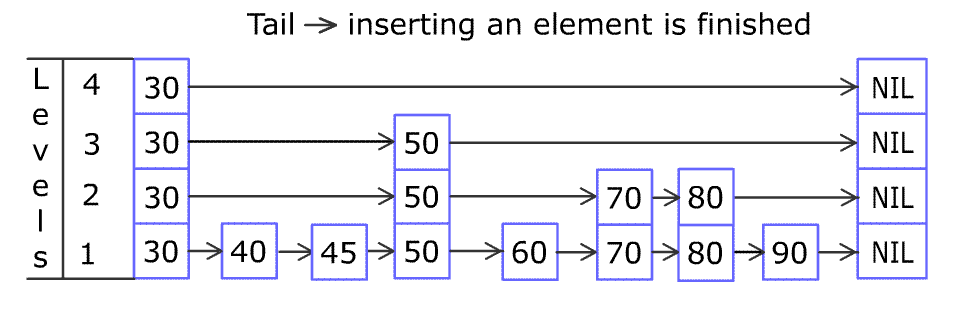
在最底层（第 0 层），如果最右边元素的前向元素的值等于搜索关键字的值，则我们找到了关键字，否则未找到。

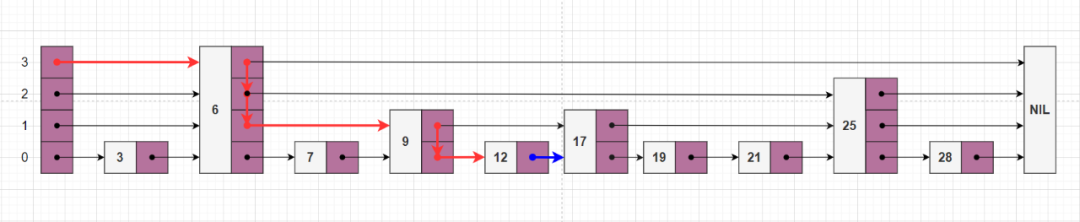
如图所示，查找关键字 17 ，红色的路线表示查找路径，其中的蓝色箭头表示最右边元素 12 的前向指针，该指针的值 17 与查找的关键字 key 相等，返回值为 key 的结点。

实现代码相当简单了：

public Node search(int key) {
    Node current = head;
    for (int i = currentLevel - 1; i >= 0; --i) {
        while (current.forwards[i] != null && current.forwards[i].key < value) {
            current = current.forwards[i];
        }
    }
    // current.key = 12
    if (current.forwards[0] != null && current.forwards[0].key == key) {
        return current.forwards[0];
    } else {
        return null;
    }
}

其中 currentLevel 表示当前跳表的层数，如上图中的 currentLevel = 4 。

跳表的删除操作

在删除元素 key 之前，使用上述查找方法在跳表中定位元素。如果找到了元素，就像我们在单链表中所做的那样，重新排列指针以删除列表中的元素。

我们从最底层（第 0 层）开始向上重新排列，直到 update[i] 的下一个元素不是 key 。删除元素后，可能会导致跳表层数 currentLevel 的降低，最后对其进行更新即可。

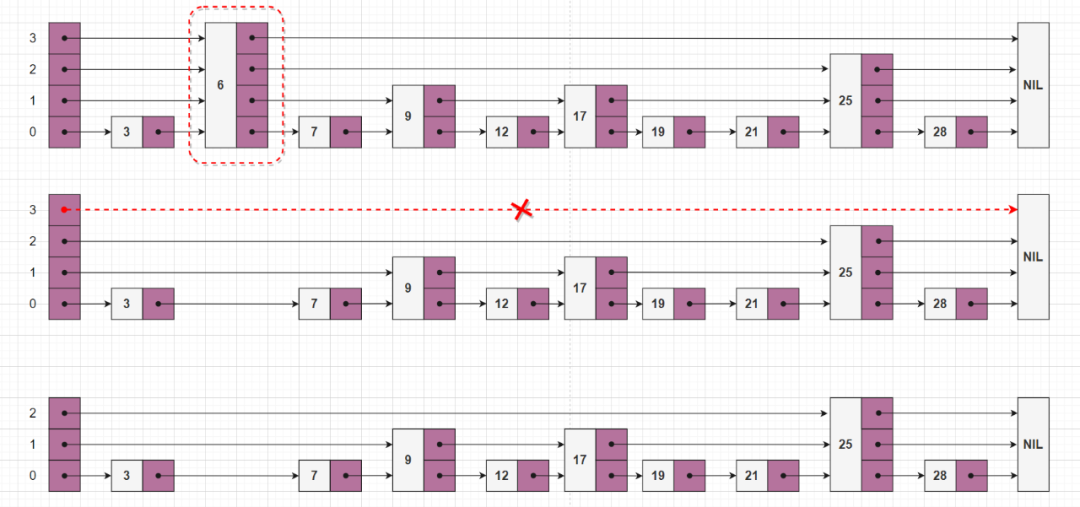
如上图所示，删除 key = 6 的结点之后，第三层没有了元素(红色虚线箭头)。所以我们将跳表的层数减 1。

public void delete(int key) {
    Node[] update = new Node[currentLevel];
    Node current = head;
    // 查找要删除结点的前序结点并保存至 update[] 中
    for (int i = currentLevel - 1; i >= 0; --i) {
        while (current.forwards[i] != null && current.forwards[i].key < key) {
            current = current.forwards[i];
        }
        update[i] = current;
    }
    // 将 update[] 的前向结点设置为要删除结点的forwords[i]
    if (current.forwards[0] != null && current.forwards[0].key == key) {
        for (int i = currentLevel - 1; i >= 0; --i) {
            if (update[i].forwards[i] != null && update[i].forwards[i].data == key) {
                update[i].forwards[i] = update[i].forwards[i].forwards[i];
            }
        }
    }
    // 更新跳表的层数
    while (currentLevel > 1 && head.forwards[currentLevel] == null) {
        currentLevel--;
    }
}

复杂度分析

空间复杂度

跳表的 期望空间复杂度 为。

在最坏的情况下，每一层有序链表等于初始有序链表，即跳表的 最差空间复杂度 为。

时间复杂度

跳表的查找、插入和删除操作的时间复杂度均取决于查找的时间，查找的 最坏时间复杂 为。

平均时间复杂度 为。大家就当二分查找。

当然按照论文中的证明，没有这么简单了。

跳表的应用

适用场景：节点插入和删除操作比较少，查询频次较多的情况。

使用跳表的产品：

Lucene, elasticSearch
Redis：Redis sorted set的内部使用 HashMap 和跳表(SkipList)来保证数据的存储和有序，HashMap 里放的是成员到 score 的映射，而跳跃表里存放的是所有的成员，排序依据是 HashMap 里存的 score ，使用跳表的结构可以获得比较高的查找效率，并且在实现上比较简单。
HBase MemStore 内部数据存储

推荐阅读

国产小众浏览器因屏蔽视频广告，被索赔100万（后续）

年轻人“不讲武德”：因看黄片上瘾，把网站和786名女主播起诉了

中国联通官网被发现含木马脚本，可向用户推广色情APP

张一鸣：每个逆袭的年轻人，都具备的底层能力

关于程序员大白

程序员大白是一群哈工大，东北大学，西湖大学和上海交通大学的硕士博士运营维护的号，大家乐于分享高质量文章，喜欢总结知识，欢迎关注[程序员大白]，大家一起学习进步！