图解：什么是AVL树？（上篇）

来源：景禹

作者：景禹

平衡二叉树基础篇

什么是平衡二叉树？

平衡二叉树（Balanced Binary Tree 或 Height-Balanced Tree）又称为 AVL 树，其实就是一颗 平衡的二叉排序树 ，解决了昨天讲的二叉排序树的不平衡问题，即斜树。AVL树或者是一颗空树，或者是具有下列性质的二叉排序树：

它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过 1 。

什么是平衡因子？

平衡二叉树上结点的 平衡因子  BF(Balanced Factor) 定义为该结点的左子树深度减去它的右子树的深度，平衡二叉树上所有结点的平衡因子只可能是 -1，0，1。

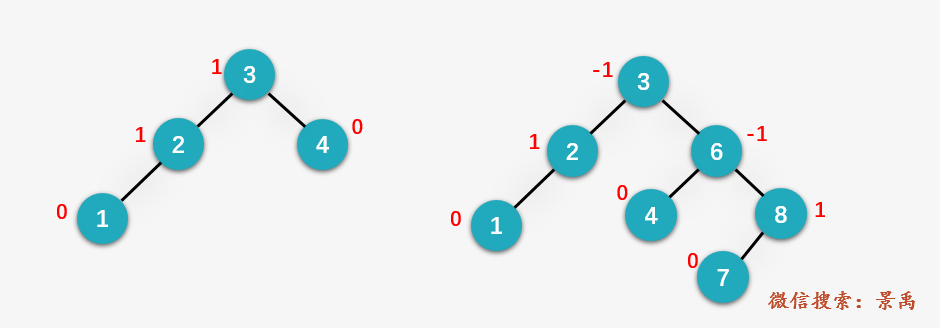
上面的两个树就是典型的平衡二叉树，首先它是一颗二叉排序树，其次每一个结点的平衡因子都是 -1，0，1三个数当中的一个。比如上面的左图，红色的数字为结点的平衡因子，对于任意一个叶子结点而言，其左右孩子都为空，左子树的深度为 0 ，右子树的深度为 0 ，所以 AVL树当中的叶子结点的平衡因子都是 0 ；其他结点的平衡因子同样通过左子树深度减去右子树深度可以求得，比如上图中 左侧 的AVL树中，结点 3 的 左子树深度为 2，右子树深度为1 ，所以结点3的平衡因子就是 1；上图中 右侧 的AVL树中，结点 3 的左子树深度为2，右子树深度为3，则平衡因子为 2 - 3 = -1 。再来看看不平衡的情况。

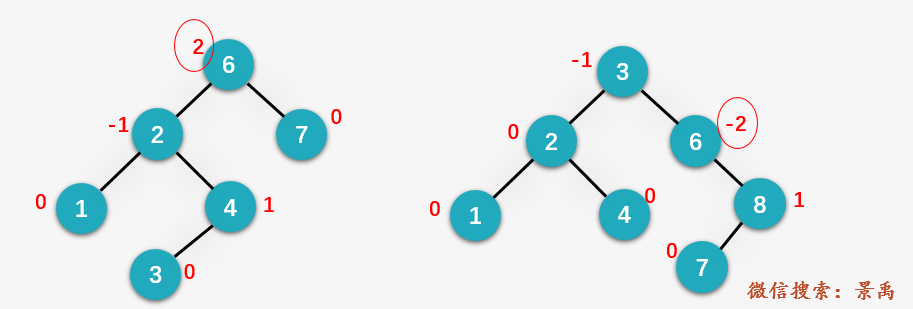
上图中就是不平衡的二叉排序树，非AVL树 。上图 左侧 的树中，结点 6 的平衡因子为 2，该平衡因子是结点 6 左子树深度 3 减去右子树深度 1 所得；右侧 的树中，结点 6 的左子树深度0减去右子树深度2，即为-2， 所以这两棵树都不是平衡二叉树。

什么是左旋？什么又是右旋？

为了确保每一次插入操作后，树仍然是一颗 AVL 树，我们就需要对之前分享的 BST(二叉排序树) 的插入操作进行平衡操作，而左旋和右旋操作就是保证二叉排序树特性的基础之上，维持每一次插入操作后树一直保持AVL树的基本操作。

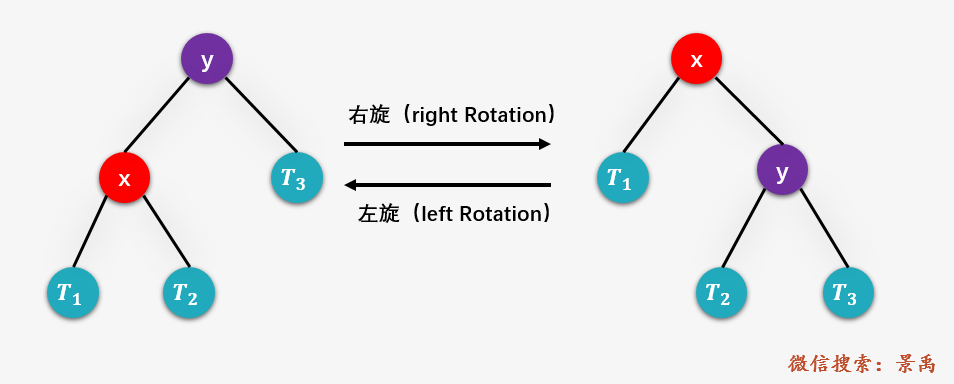
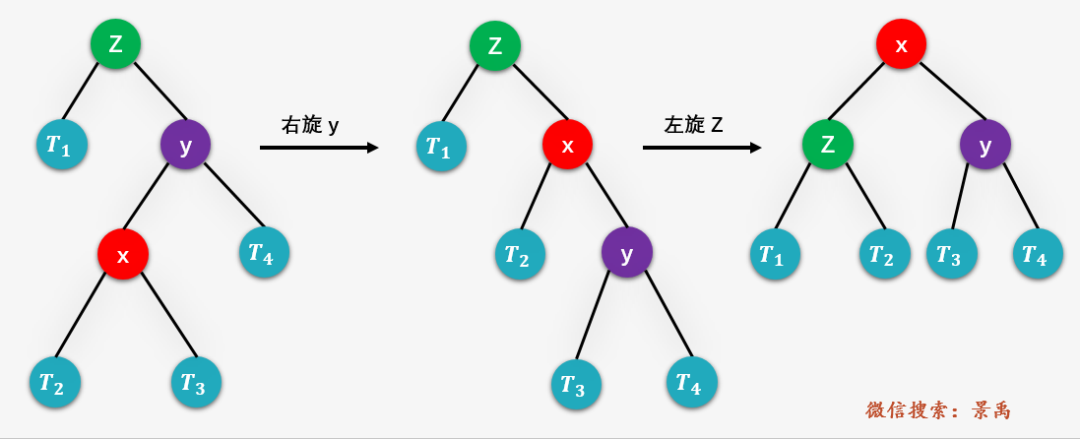
、 和 分别表示 或 的子树。右旋操作 将 的右子树 作为 的左子树，然后将 作为 的右子树。这样做的原因何在？还记得平衡二叉树的特性是，对于树中的每一个结点，其左子树中的结点均比结点的值小，右子树中结点的值均比结点的值大，那么对于上图 左侧 的树而言， 的右子树 的值一定比   的值大且一定比根结点 的值小，所以将 的右子树 的值作为根结点 的值并不会破坏二叉排序树的特性，此外 的值大于其左孩子 的值，将 作为根结点时， 作为右孩子也不会破坏二叉树特性，而所谓右旋，是因为结点变化有一个向右的动作。左旋操作则是右旋操作的逆过程 。但不论如何，上面两颗树的中序遍历结果，，一定是一致的，也就是任何时候都满足 二叉排序树 的特性。

平衡二叉树的插入操作

对平衡二叉树的插入操作而言，其本质上比二叉排序树（BST）的插入操作多了一个平衡操作，解决了二叉排序树插入操作可能出现的斜树，不平衡问题。

我们以插入一个结点 为例进行说明平衡二叉树插入操作的具体算法步骤。

1. 对结点 执行标准的二叉排序树的插入操作；
2. 从结点 开始，向上回溯，找到第一个不平衡的结点（即平衡因子不是 -1，0或1的结点） ； 为从结点 到结点 的路径上， 的孩子结点（这里强调路径,所以一定要注意奥 ）； 是从结点 到结点 的路径上， 的孙子结点 。
3. 然后对以 为根结点的子树进行平衡操作，其中 x、y、z 可以的位置有一种情况，平衡操作也就处理以下四种情况：
• y 是 z 的左孩子，x 是 y 的左孩子 （Left Left ，LL )；
• y 是 z 的左孩子，x 是 y 的右孩子 （Left Right ，LR )；
• y 是 z 的右孩子，x 是 y 的右孩子 （Right Right ，RR )；
• y 是 z 的右孩子，x 是 y 的左孩子 （Right Right ，RL )；

在所有的四种情况下，我们只需要重新平衡以 z 为根的子树，并且保证以 z 为根的子树的高度（在适当旋转之后）与 w 插入之前的高度相同，整颗树就变得平衡了。

第一种情况：LL

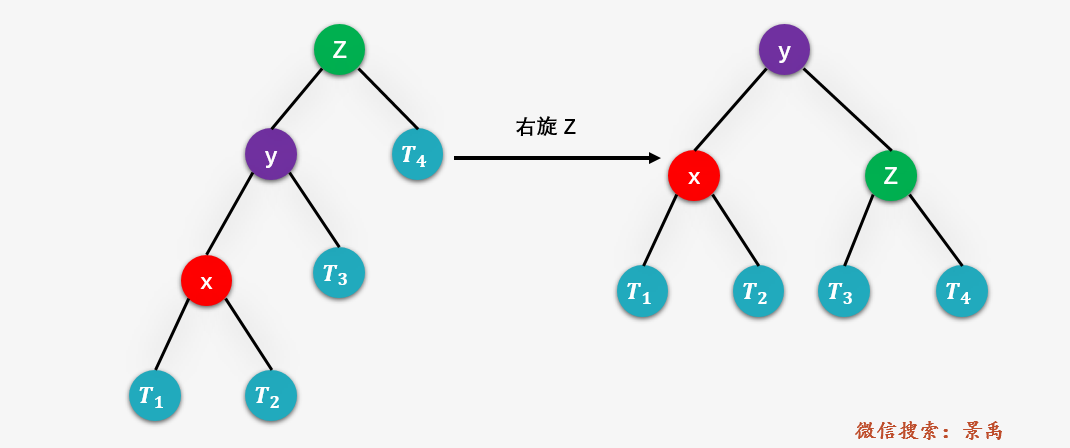
第二种情况：LR

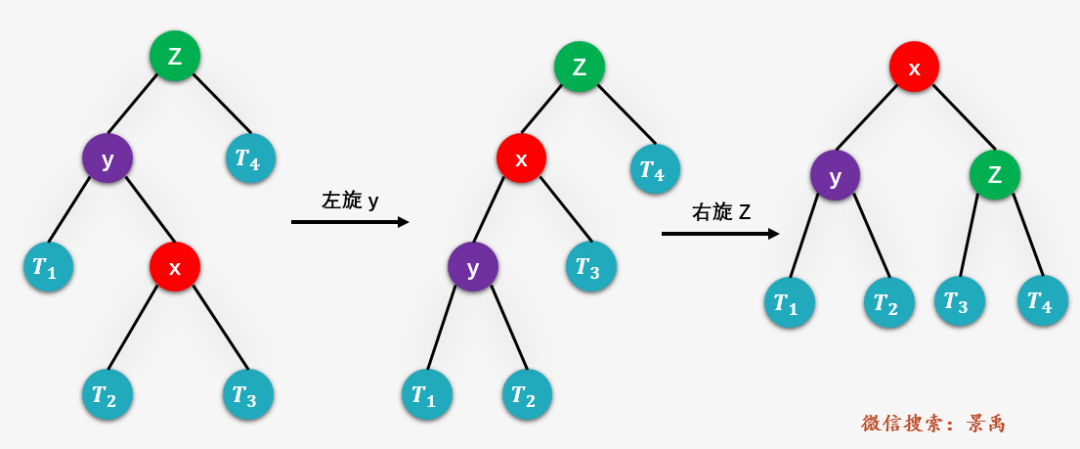
第三种情况：RR

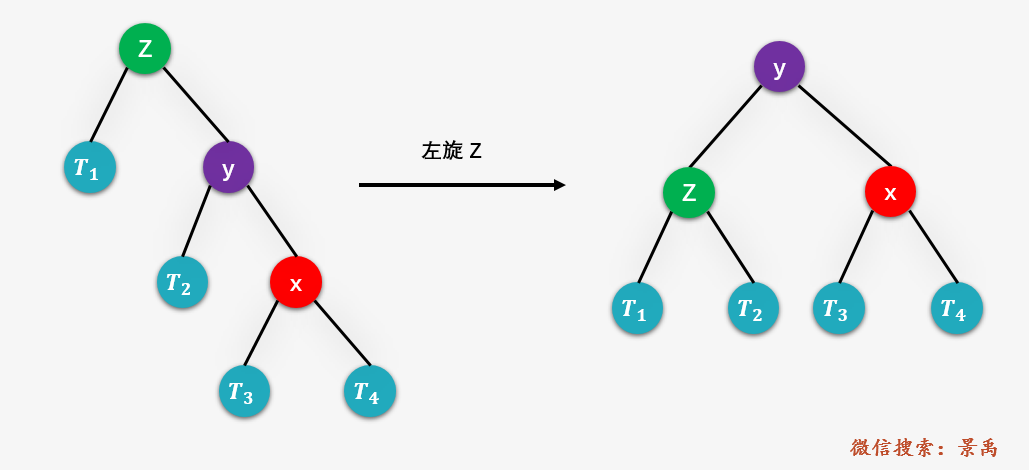
第四种情况：RL

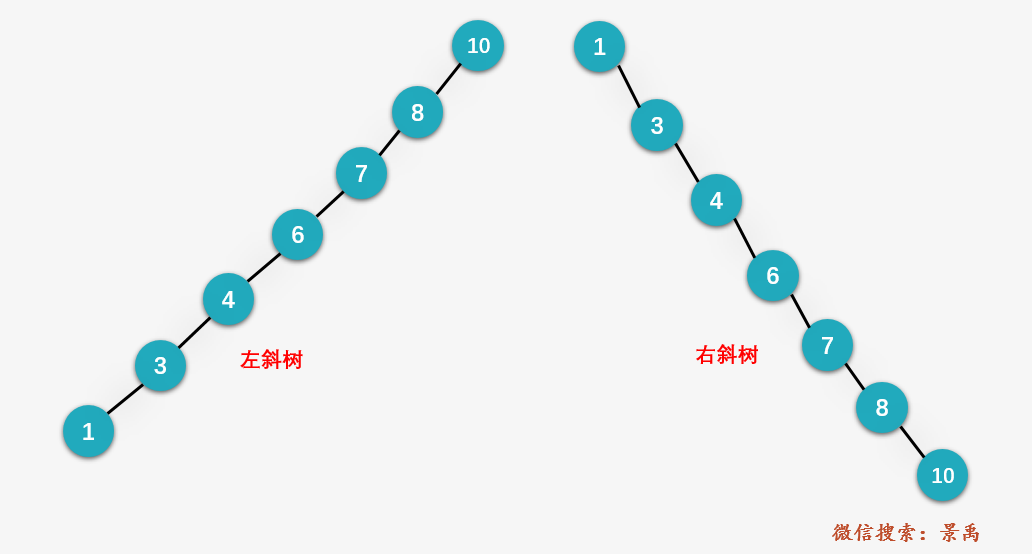
上面就是二叉排序树在极端情况下出现的问题，现在我们以 右斜树 的插入序列，一起进行一遍平衡二叉树的插入操作。初始的插入序列为：

第一步：插入结点 1 ，显然一颗空树或者只包含一个结点的树为平衡二叉树，什么都不做。结点 1 的左右子树都为空，则平衡因子等于 左子树的深度0减去右子树深度0 ，即为 0 。

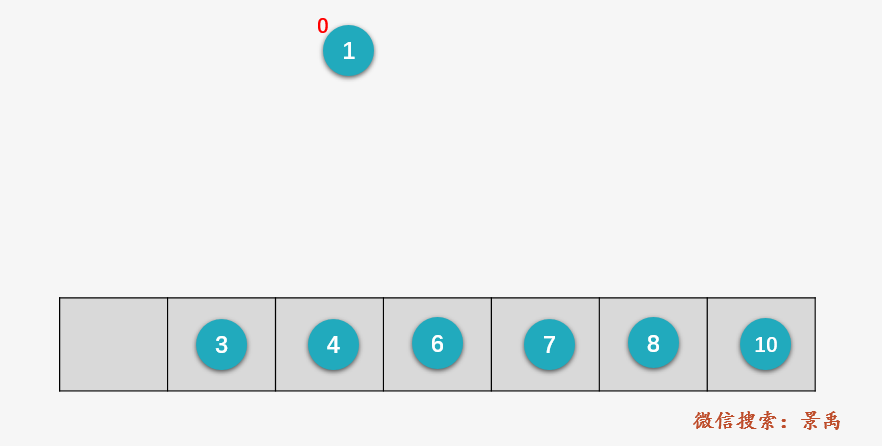
第二步：插入结点 3 ，先执行 BST的标准插入 ，3 的值比 1 大，插入 1 的右子树，又因为 1 的右子树为空，则直接将 3 作为 1 的右孩子插入。（由于二叉排序树的插入操作之前已经讲的很清楚了，后面就不再像刚才啰嗦 ）。3 为叶子结点，平衡因子为 0 ；此时 1 的左子树深度为0减去右子树深度1，即平衡因子为 -1 ，整棵树依旧平衡。

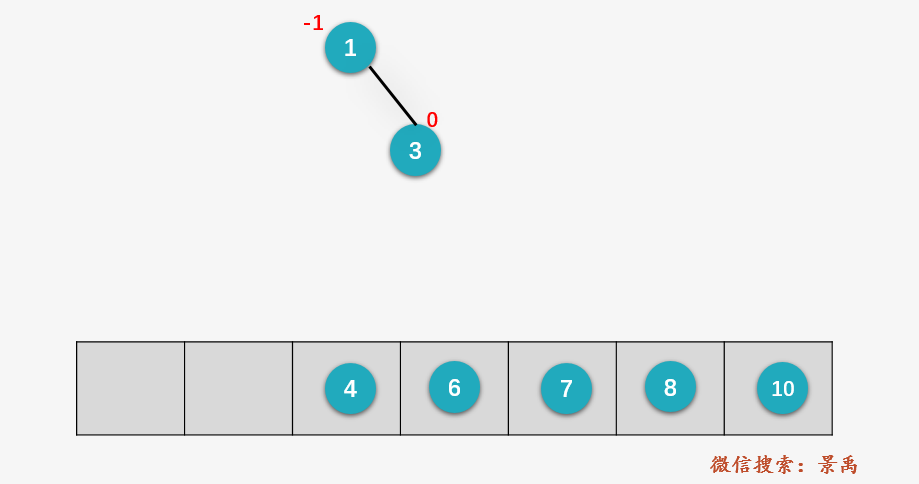
第三步：插入结点 4 ，先执行 BST的标准插入 ，然后计算更新结点的平衡因子（图中使用红色字体表示），从插入结点 4 向上回溯，找到第一个不平衡的结点 1 (相当于算法描述中的 z ) 的平衡因子为 -2 ，并不满足平衡二叉树的特性，找到从结点 4 到结点 1 的路径上结点 1 的孩子结点 3  (相当于算法描述中的 y )，孙子结点 4 （相当于算法描述中的 x )，这显然就是我们上面的 RR 情况；

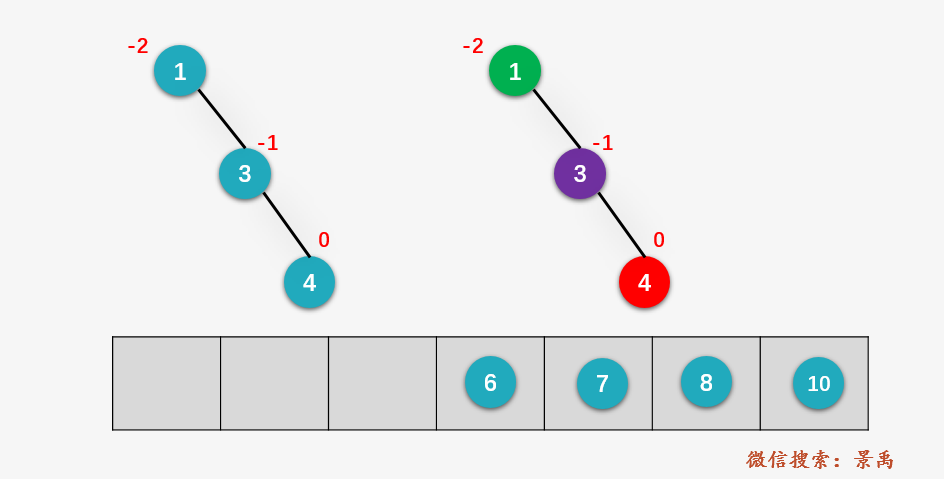
第四步：对结点 1 进行 左旋操作 。

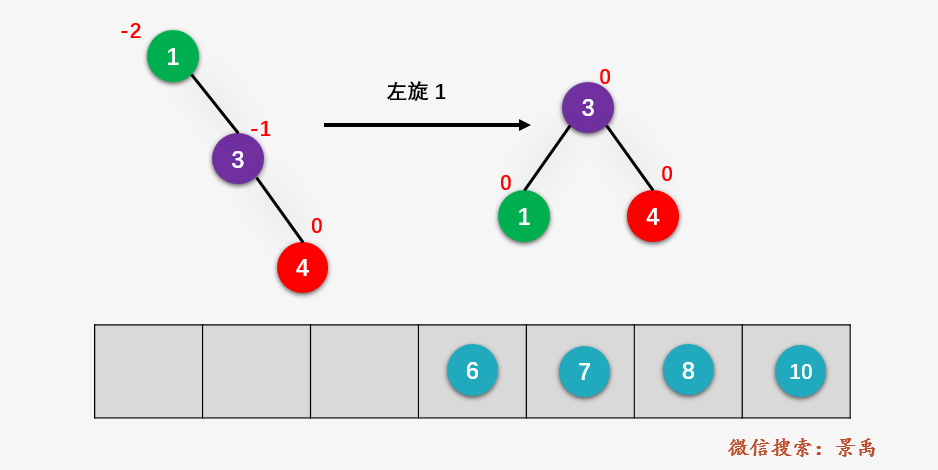
第五步：插入结点 6 ，并更新平衡因子，发现此时为平衡二叉树，什么都不做。

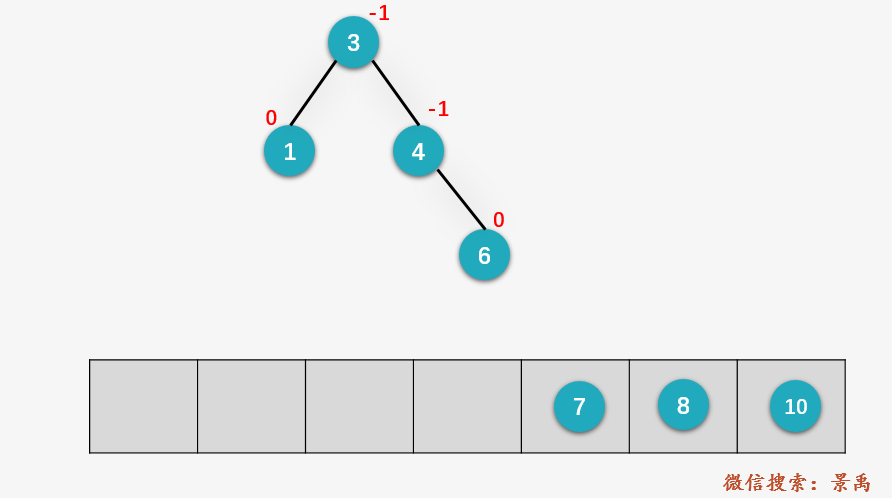
第六步：插入结点 7 ，并更新平衡因子，从结点 7 向上回溯，找到相应的 z、y、x ，对应于结点 4、6、7。

第七步：进行平衡操作，并更新结点的平衡因子：

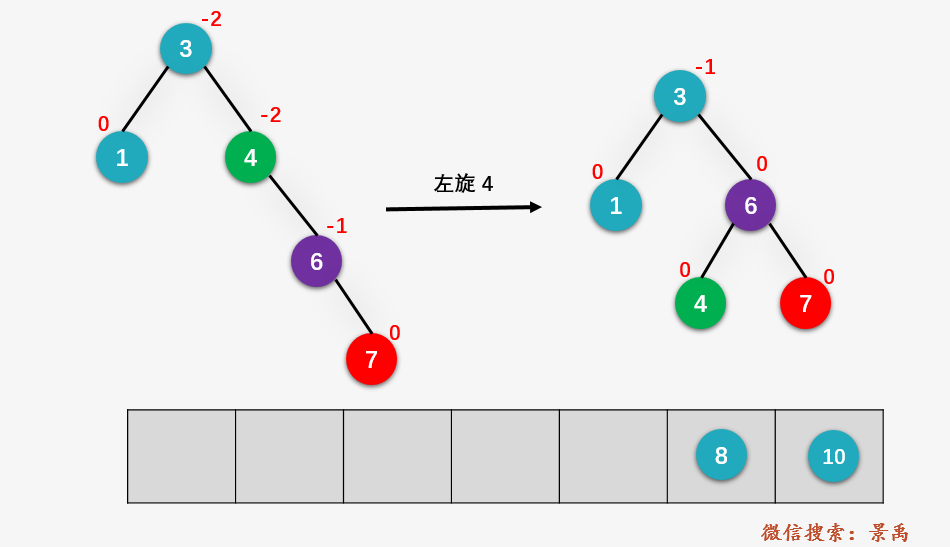
第八步：插入结点 8 ，并更新平衡因子，从节点 8 向上回溯找到相应的 x、y、z ，即结点 3、6，7 。

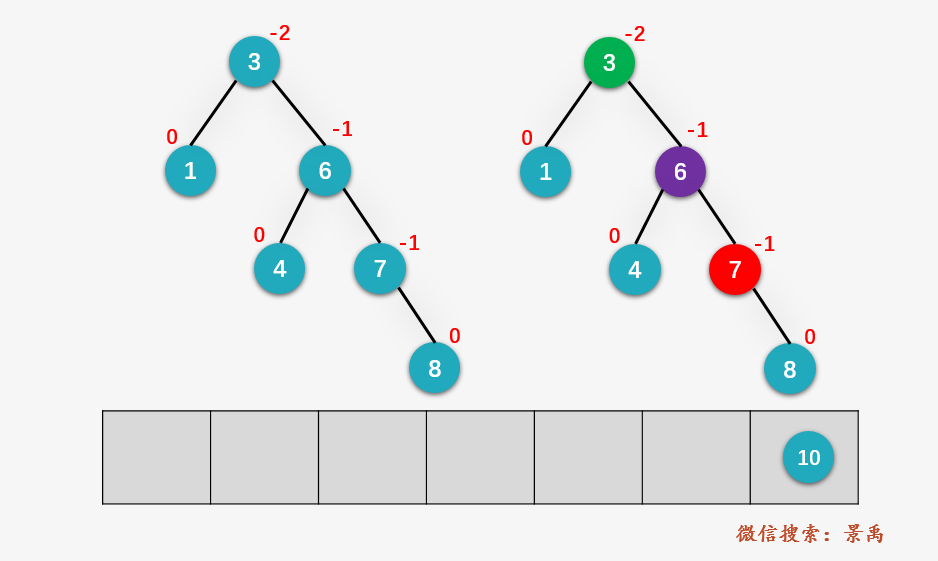
第九步：对结点 3 进行 左旋操作 。

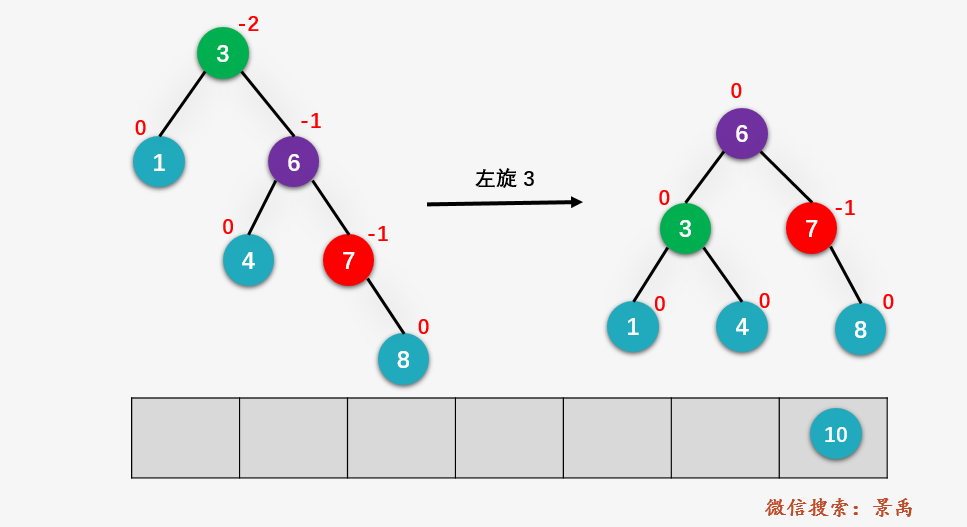
第十步：插入结点 10 ，并更新结点的平衡因子，从节点 10 向上回溯找到第一个不平衡的结点 7 ，并找到对应的孩子结点 8 和孙子结点 10 。

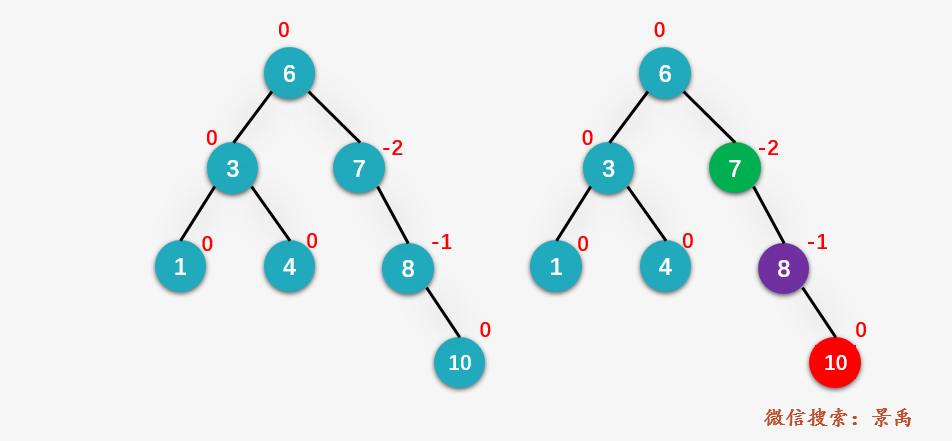
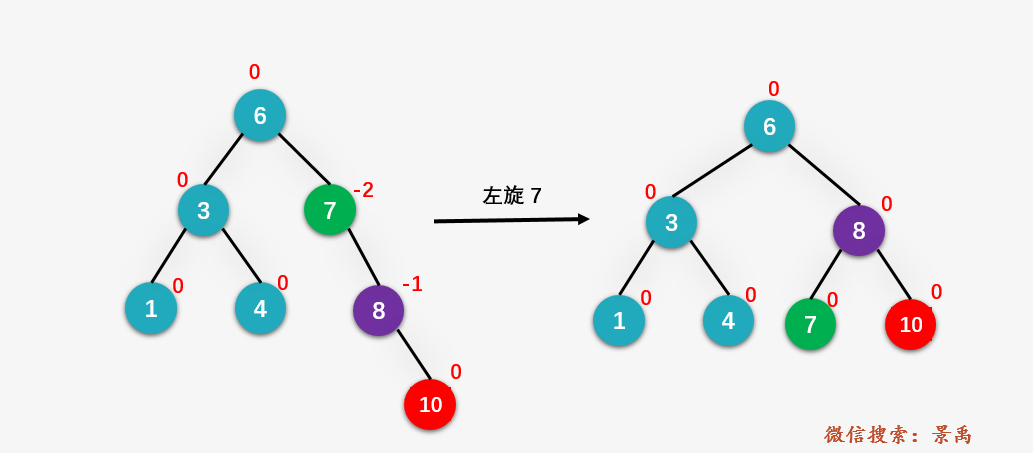
第十一步：对结点 7 进行左旋操作：

LL的情况

首先我们有如下约定：

现在我们用下图进行说明：

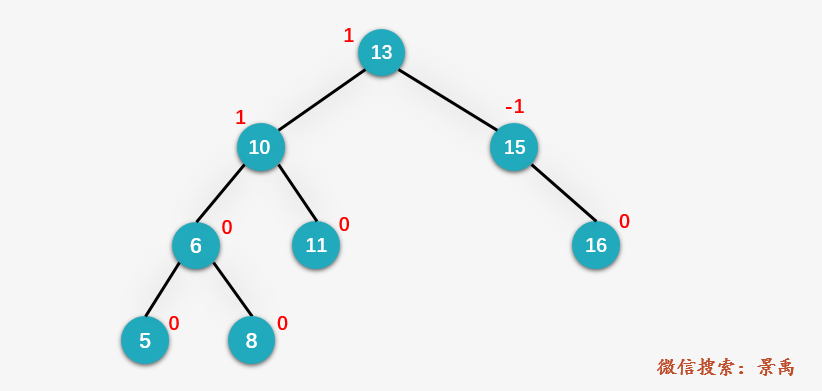
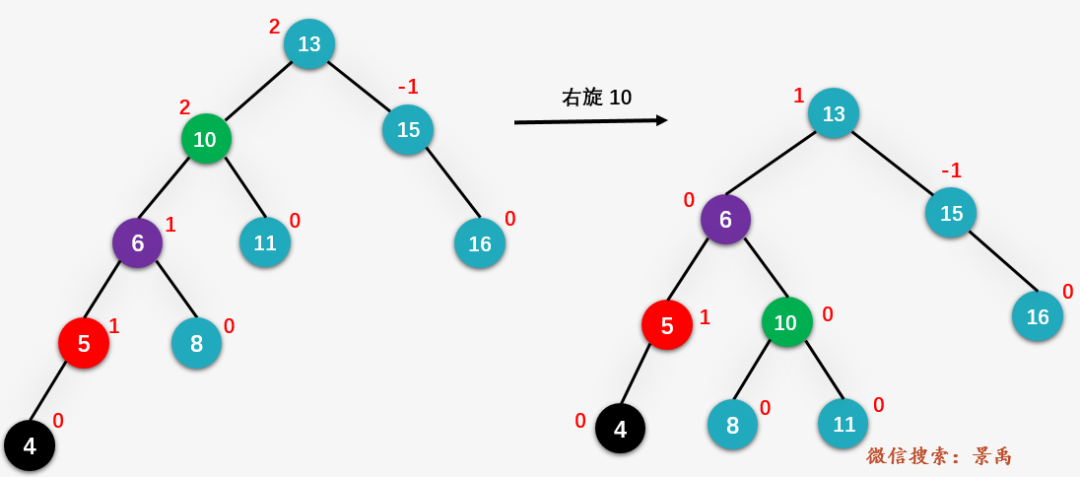
上图就一个平衡二叉树，现在我们插入值为 4 的结点（进行标准的BST插入操作），从结点 4 向上回溯，找到相应的  z、y、x  ，如下图所示：

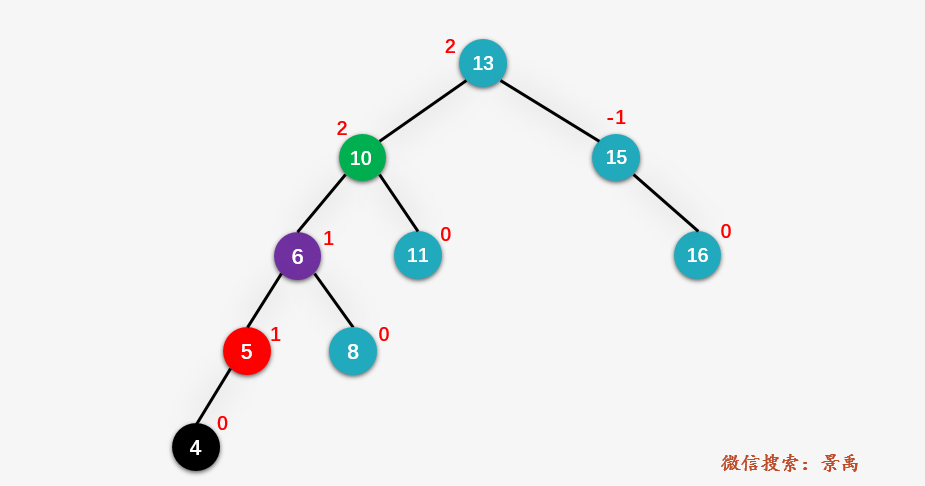
然后对结点 10 进行右旋操作：

LR的情况

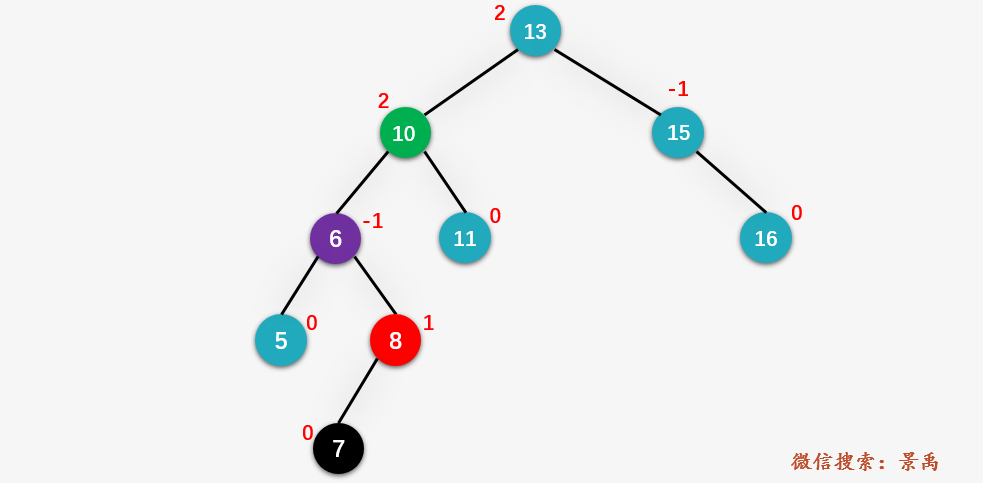
同样以下图为例：

现在我们向该平衡二叉树当中插入值为 7 的结点，从结点 7 向上回溯，找到相应的  z、y、x  ，如下图所示：

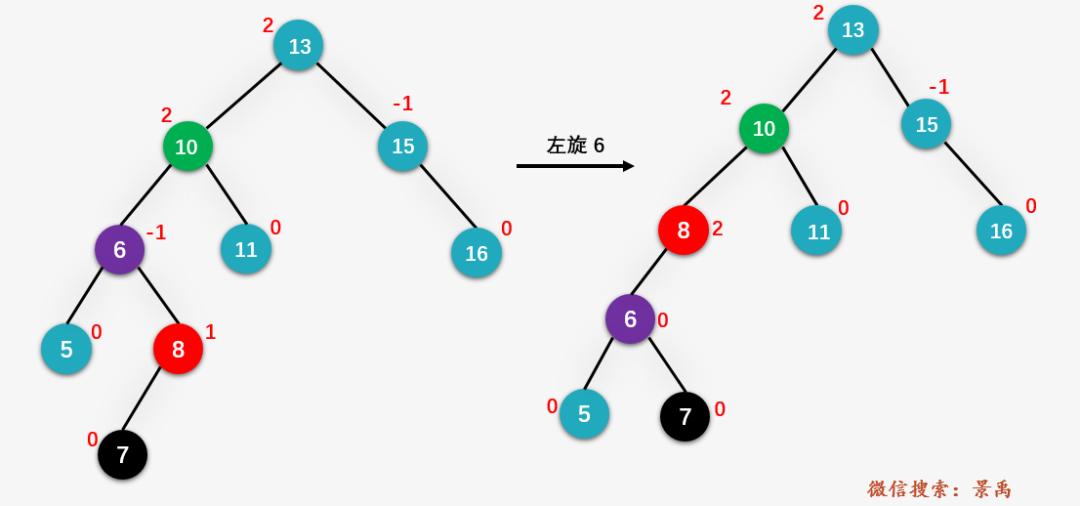
根据 LR 的情况，先左旋 y (即图中的结点 6 )：

然后右旋 z （即图中的顶点 10 ）：

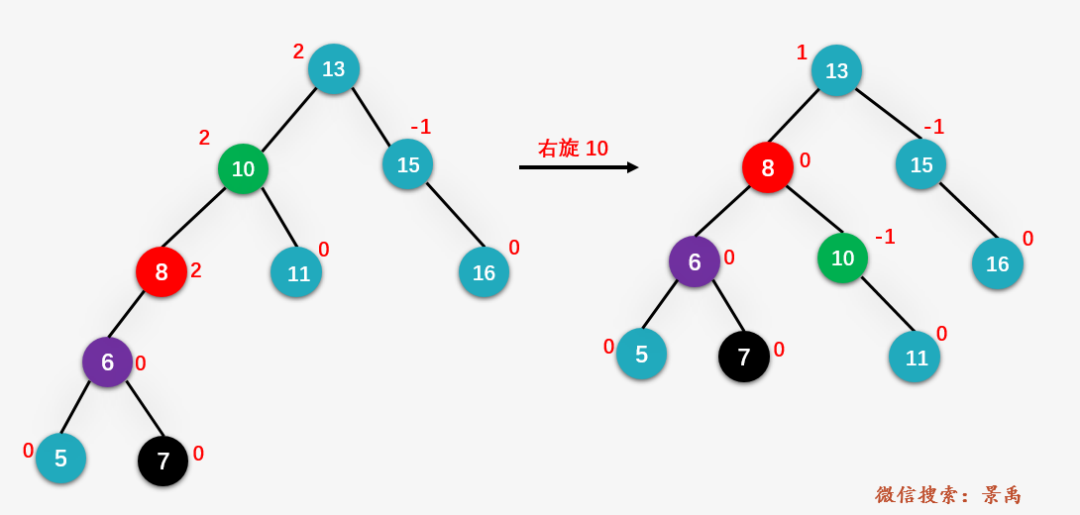
这样我们就得到对应的平衡二叉树，可以对应下图再温习一下 LR 的情况。

RL的情况

我们以下图为例进行说明:

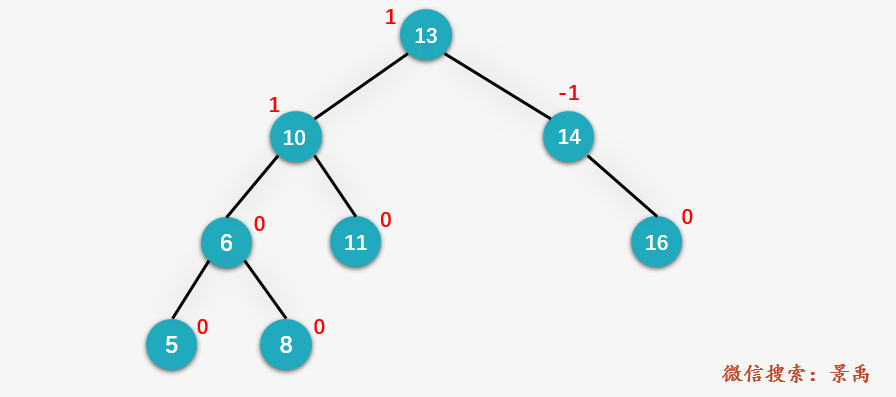
此时向平衡二叉树当中插入结点 15 ，插入过程就是标准的二叉排序树的过程，不再累述。并更新结点的平衡因子：

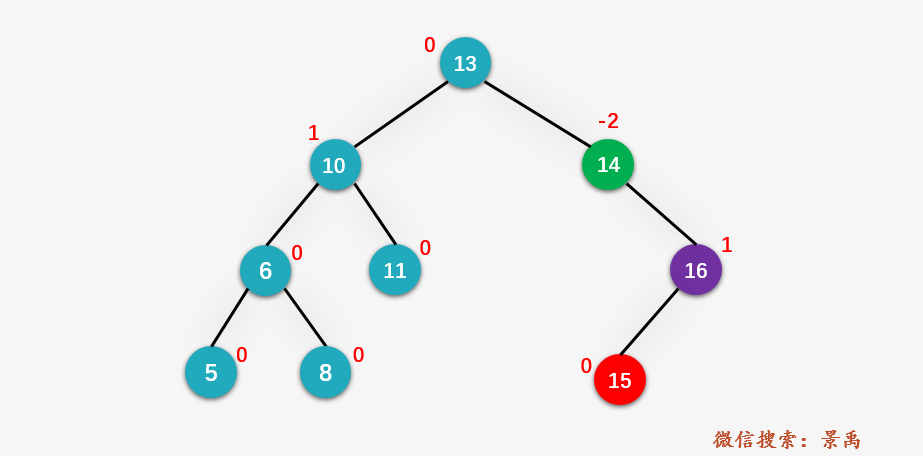
第一步：右旋结点 x (即图中的结点 15 )

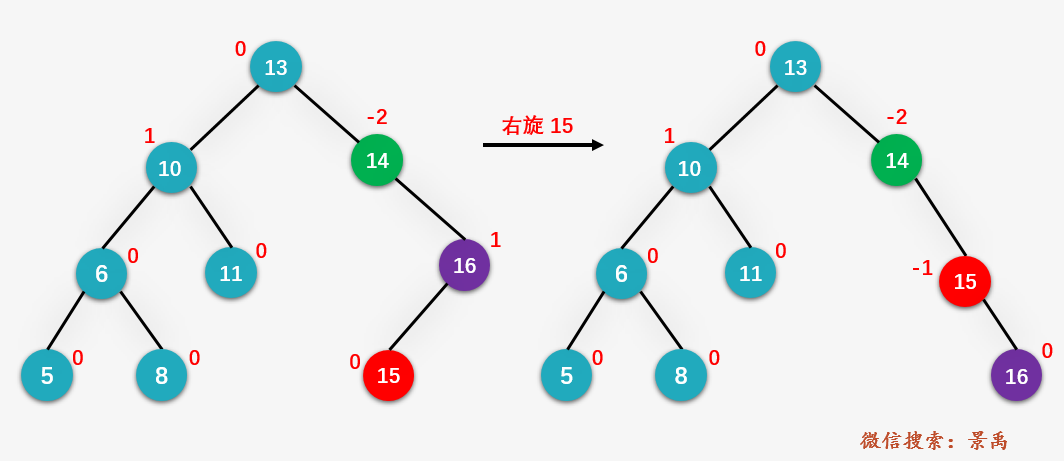
第二步：左旋结点 Z (即图中的结点 14 )

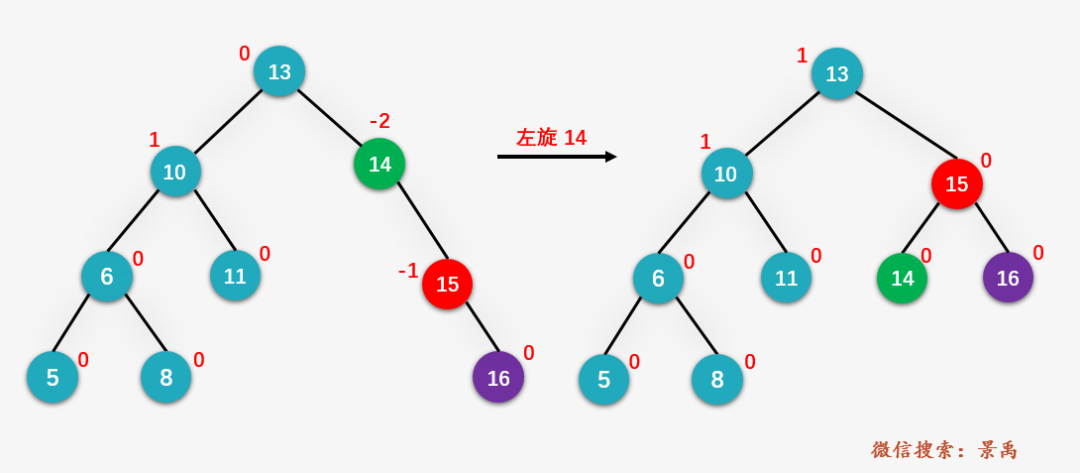
整个过程和之前提到过的 RL 的演示图一致，只不过对应的  均为空而已，各位小禹禹可不能被忽悠奥，要灵活使用。

时间复杂度分析

因为 AVL 树上的结点的左右子树的深度之差都不超过 1，也就是取值只能是 -1，0，1 ，则 AVL 树的深度和 是同数量级的（其中 n 为结点个数）。因此平衡二叉树的平均查找长度和 也是同数量级的，二叉排序树的插入和查找的时间复杂度即为 量级。

平衡二叉树（AVL）插入操作的实现

在实现平衡二叉树的插入操作时，我们采用二叉排序树（BST）的插入操作的递归实现。在 BST 的递归实现中，插入结点之后，可以自插入结点向上回溯的方式逐一获得指向祖先结点的指针（事实上你讲递归的过程用栈来理解就更加清楚了，首先从根结点开始，进行判断，一直到插入结点的位置，将从插入结点到根结点经过的路径压栈，那么回溯的时候，从插入结点自然可以回溯到根结点）。因此，我们就不需要专门设置一个用于保存父结点的指针了。递归代码本身向上回溯并访问从根结点到插入结点的路径上的所以结点的祖先。

1. 执行标准的平衡二叉树的插入操作；
2. 更新当前结点（从根结点到新插入结点的路径上经过的结点）的深度。
3. 获取当前结点的平衡因子（左子树的深度 - 右子树的深度）。
4. 如果平衡因子大于 1 ，则当前结点是不平衡结点，且当前结点的子树存在 LL 或 LR 的情况；检查是否是 LL 的情况，将新插入结点的值与当结点的左孩子的值进行比较，如果小于则是 LL 的情况，否则是 LR 的情况。
5. 如果平衡因子小于 -1 ，则当前结点是不平衡结点，且当前结点的子树存在 RR 或 RL 的情况；检查是否是 RR 的情况，判断新插入结点的值是否大于当前结点的右孩子的值，如果大于，则属于 RR 的情况，否则为 RL 的情况。

平衡二叉树插入操作代码：

左旋与右旋操作： 小禹禹可以对照着下面的图看代码，就会特别清晰。

//RL的情况下，对以 y 为根的结点进行右旋操作。
struct Node *rightRotate(struct Node *y) 
{ 
 //保存y的左孩子 x
 struct Node *x = y->left; 
 //保存x的右孩子 T2
 struct Node *T2 = x->right; 

 // 有旋转操作，将x的右孩子设置为y,将y的左孩子设置为T2 
 x->right = y; 
 y->left = T2; 

 // 更新结点结点x和结点y的深度
 y->height = max(height(y->left), height(y->right))+1; 
 x->height = max(height(x->left), height(x->right))+1; 

 // 返回新的结点x.
 return x; 
} 

// 左旋以 x 为根结点的子树。
struct Node *leftRotate(struct Node *x) 
{ 
 //保存x的右孩子 y
 struct Node *y = x->right; 
 //保存y的左孩子T2
 struct Node *T2 = y->left; 

 // 左旋操作，将y的左孩子设置为x,将x的右孩子设置为T2
 y->left = x; 
 x->right = T2; 

 // 更新结点x和结点y的深度。
 x->height = max(height(x->left), height(x->right))+1; 
 y->height = max(height(y->left), height(y->right))+1; 

 // 返回新的根结点y. 
 return y; 
} 

计算平衡因子： 结点的左子树深度减去右子树深度。

int getBalance(struct Node *N) 
{ 
 if (N == NULL) 
  return 0; 
 return height(N->left) - height(N->right); 
} 

平衡二叉树的插入操作

struct Node* insert(struct Node* node, int key) 
{ 
 /* 1.执行标准的二叉排序树的插入操作 */
 if (node == NULL) 
  return(newNode(key)); 

 if (key < node->key) 
  node->left = insert(node->left, key); 
 else if (key > node->key) 
  node->right = insert(node->right, key); 
 else //二叉排序树中不允许等于的情况。
  return node; 

 /* 2. 更新当前结点node的深度 */
 node->height = 1 + max(height(node->left), 
      height(node->right)); 

 /* 3. 获取当前结点的平衡因子，并判断当前结点是否是平衡结点 */
 int balance = getBalance(node); 

 // 如果当前结点是不平衡结点，则分以下四种情况处理

 // LL的情况，对当前不平衡结点（相当于z）进行右旋操作 
 if (balance > 1 && key < node->left->key) 
  return rightRotate(node); 

 // RR的情况，对当前不平衡结点进行左旋操作。
 if (balance < -1 && key > node->right->key) 
  return leftRotate(node); 

 // LR的情况，对不平衡结点(结点z)的左孩子(结点y)进行左旋操作
 //，然后对当前结点进行右旋操作。
 if (balance > 1 && key > node->left->key) 
 { 
  node->left = leftRotate(node->left); 
  return rightRotate(node); 
 } 

 // RL的情况，对不平衡结点(结点z)的右孩子(结点y)进行右旋操作
 //，然后对当前结点进行左旋操作。
 if (balance < -1 && key < node->right->key) 
 { 
  node->right = rightRotate(node->right); 
  return leftRotate(node); 
 } 

 /* 返回结点指针 */
 return node; 
} 

LeetCode题解

题目来源于 110. 平衡二叉树 Balanced Binary Tree

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

输入输出示例

示例一：

给定二叉树 [3,9,20,null,null,15,7]

返回 true

示例二：

给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false 。

题目解析

考虑一颗二叉树是否高度平衡，我们需要检查下面的这些条件：

一颗空树必然是高度平衡的。一颗非空的树 是高度平衡的，当且仅当满足下面三个条件（递归定义）：

1. 树 的左子树是平衡的；
2. 树 的右子树是平衡的；
3. 左右子树的高度之差不超过1；

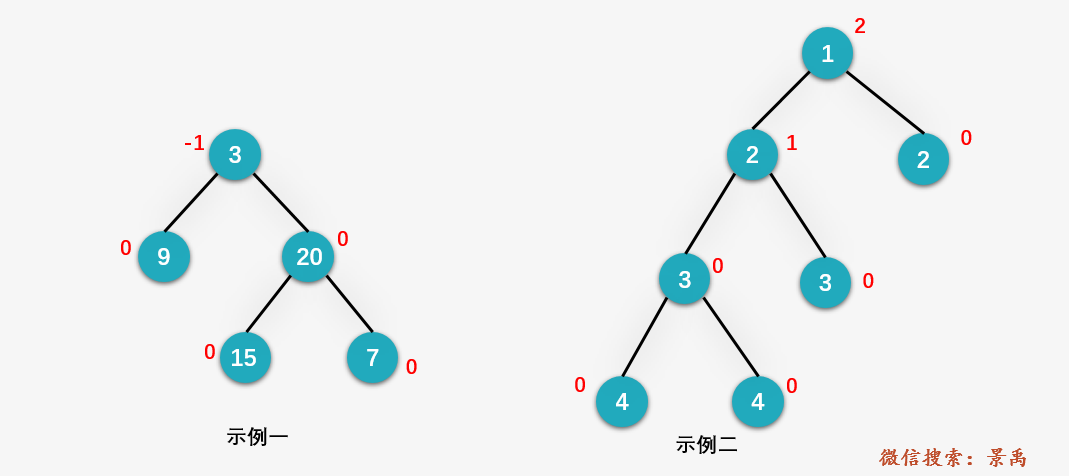
根据上面对于高度平衡的定义，显然示例一当中的树是高度平衡的；示例二中的树不是高度平衡的，因为结点1的左子树与右子树的深度之差为2，大于1。

方法一

检查一颗二叉树是不是高度平衡，则对二叉树的结点检查其左右子树的高度之差是否超过 1，超过 1则返回false，否则返回true;

int abs(int x){
    if(x < 0){
        return -x;
    }
    return x;
}
int max(int x, int y){
    return (x >= y) ? x : y;
}
//计算node的高度
int height(struct TreeNode* node){
    if(node == NULL)
    {
        return 0;
    }
    return 1 + max(height(node->left), height(node->right));
}
//判断二叉树是否平衡
bool isBalanced(struct TreeNode* root){
    int lh; //左子树高度
    int rh; //右子树高度
 
    //树为空返回true;
    if(root == NULL)
        return 1;
 //获得左子树深度
    lh = height(root->left);
    //获得右子树深度
    rh = height(root->right);
    //判断左右子树高度之差是否小于1，并且结点的左右子树平衡，返回true;
    if(abs(lh - rh) <= 1 && isBalanced(root->left) && isBalanced(root->right)){
        return 1;
    }
    return 0;
}

方法二（对方法一优化）

但是上面的方法存在性能上的问题，当输入是一颗斜树的时候，其时间复杂度将变成 。问题在于我们判断二叉树是否平衡的函数 isBalanced() 当中嵌套了一个计算树的高度的函数height() ，这样以来，当树为一颗斜树的时候，时间复杂度就会达到 。解决的办法就是将这两个函数合并，取消单独调用的height（）函数，而是在递归进行判断的时候计算树的高度。

int abs(int x){
    if(x < 0){
        return -x;
    }
    return x;
}

bool isBalancedUtil(struct TreeNode* root, int* height){
    int lh; //保存左子树的高度
    int rh; //右子树的高度

    int l = 0; //左子树是否平衡标志
    int r = 0; //右子树是否平衡标志

    if(root == NULL){
        *height = 0;
        return 1;
    }
    //递归判断左右子树是否平衡
    l = isBalancedUtil(root->left, &lh);
    r = isBalancedUtil(root->right, &rh);

    //计算树的高度，左右子树高度较大者加1
    *height = ((lh >= rh) ? lh : rh) + 1;
 
    //如果左右子树高度之差大于等于2，返回false;
    if(abs(lh - rh) >= 2){
        return 0;
    }
    //否则返回左右子树平衡标志的与
    return l && r;
}
bool isBalanced(struct TreeNode* root){
    int height = 0;
    return isBalancedUtil(root,&height);
}

温馨提示，需要AVL树实现代码的小禹禹，后台回复 「 AVL 」就可以获得（包括Python、Java、C++ 和 C的实现）。