「@Author：Runsen」

❝

编程的本质来源于算法，而算法的本质来源于数学，编程只不过将数学题进行代码化。「---- Runsen」

❞

据说，放张小姐姐觉得照片可以提高阅读量，图是来源学校的2020新生。

算法，一门既不容易入门，也不容易精通的学问。

最近看了 labuladong的文章：单调栈解题模板秒杀三道算法题。

根据脑海大纲的思路，发现这是一个非常重要的题型，于是我赶紧花费点时间刷了下。

单调栈

单调栈的实质是有单调性的栈，包括单调递增栈和单调递减栈。通过栈的入栈和出栈维护一个动态的滑动窗口，然后栈顶元素是该窗口的最大值或最小值，通过一次遍历，就可以计算出所有元素的下一个较大值或较小值。

如下图，分别插入6,10,3,7,4,12的时候，单调递增栈和单调递减栈的情况：

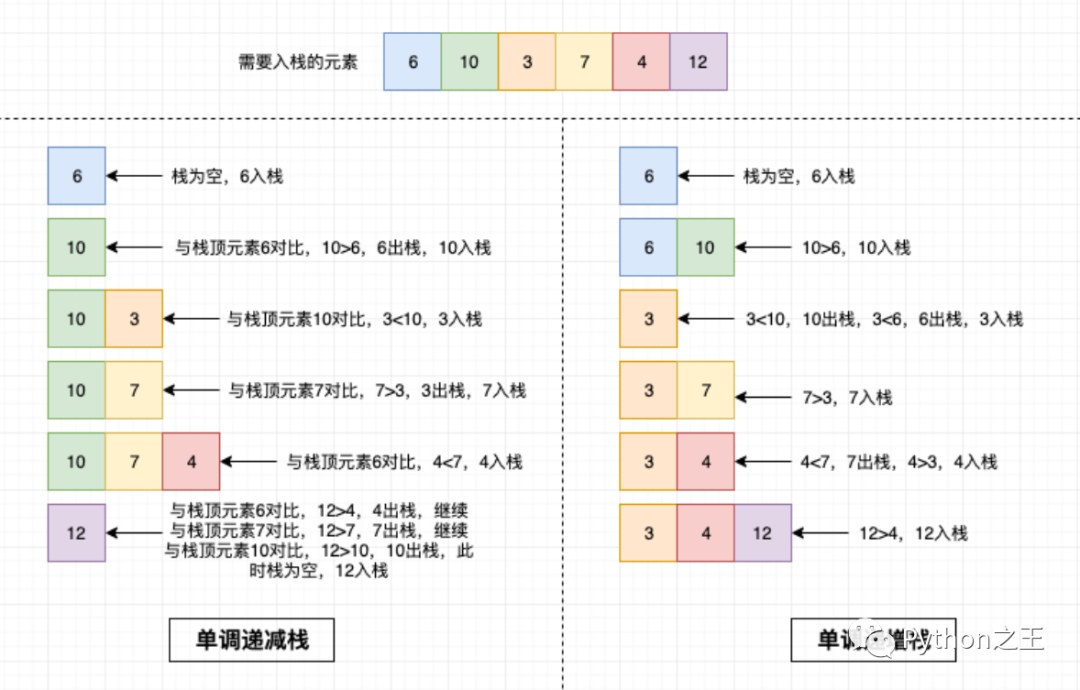
下一个更大元素

给一个int组成的array，找到下一个比当前值更大的元素组成的数组，如果找不到，填充-1，例子：nums = [44 ,15 ,22, 9 ,7, 2 ,18 ,23, 27 ]输出：[-1, 22, 23, 18, 18, 18, 23, 27, -1]

最简单的思路就是两重循环，第二次循环从当前位置往后扫，直到扫到一个比它大的数。时间复杂度。

res = []
nums = [44 ,15 ,22, 9 ,7, 2 ,18 ,23, 27 ]
for i in range(len(nums)):
    bigger = -1
    for j in range(i,len(nums)):
        if nums[i] < nums[j]:
            bigger = nums[j]
            break
    res.append(bigger)
print(res)
# [-1, 22, 23, 18, 18, 18, 23, 27, -1]

如果使用了单调栈+散列表的做法，关于单调栈+散列表的思路，可以查看Leetcode 496官方题解的动画。

更好的方法就是从左往右扫描，用一个栈记录右边的值的一个递增序列。也就是「典型的散列表+单调栈解决方法。」

思路：遍历列表，将每一个元素插入到单调栈中，如果单调栈的头部元素小于插入元素，说明单调栈的头部元素下一个最大的数，就是当插入元素。于是使用字典进行储存。最后删除该单调栈的头部元素，用插入元素替换。

dict = {}
res = []
nums = [44 ,15 ,22, 9 ,7, 2 ,18 ,23, 27 ]
for i in range(len(nums)):
    while res and res[-1] < nums[i]:
        dict[res.pop()] = nums[i]
    res.append(nums[i])
while res:
    dict[res.pop()] = -1
print(dict)
# {15: 22, 2: 18, 7: 18, 9: 18, 18: 23, 22: 23, 23: 27, 27: -1, 44: -1}
for i in range(len(nums)):
    nums[i] = dict[nums[i]]
print(nums)
# [-1, 22, 23, 18, 18, 18, 23, 27, -1]

下面，速度解决Leetcode有关下一个更大的数系列的题目。

Leetcode 496 下一个更大元素 I

输入: nums1 = [4,1,2], nums2 = [1,3,4,2]. 输出: [-1,3,-1] 解释:

对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。

对于Leetcode 496，与上面多了一个数列，其实原理都是一样。下面是解题的代码。

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        """
        方法一：先找到该元素在nums2中的位置，然后再找它之后比它大的
        时间复杂度：O(n2)
        """
        # res = []
        # for i in nums1:
        #     flag = 0
        #     bigger = -1
        #     for j in nums2:
        #         if i == j:
        #             flag = 1
        #         if flag == 1 and i < j:
        #             bigger = j
        #             break;
        #     res.append(bigger)
        # return res

        """
        方法二：为nums2维护一个字典，key为当前元素，value为该元素的下一个比其大的值
        设置一个递减栈，当遇到更大的元素时，把栈里比他小的元素都放到字典中
        查找时只需要在字典中找。时间复杂度O(n+m) 空间复杂度O(m)
        """
        hash_dict = dict()
        stack = []
        for i in nums2:
            while stack and i > stack[-1]:
                hash_dict[stack.pop()] = i
            stack.append(i)
        return [hash_dict.get(i,-1) for i in nums1]

Leetcode 503 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

思路：将数组拷贝一份放在nums数组后面，对新数组进行查找下一个最大元素，上面的解法。

提交代码的时候，发现由于存在相同的测试案例。所以散列表失效了，可以声明一个全是-1的res，如果存在更大的数，就进行替换，注意返回的时候需要取长度的一半。对于第一种暴力方法还是通过的。

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        nums = nums + nums
        stack = []
        res = [-1] * len(nums)
        for i in range(len(nums)):
            while stack and nums[i] > nums[stack[-1]]:
                small = stack.pop()
                res[small] = nums[i]
            stack.append(i)
        return res[:len(res)//2]

查看官方题解和 labuladong的文章。

官方的题解是通过进行逆序来求解。不懂思路的看官方的动画，这里不解释，这种想法很少人知道，具体实现代码如下。

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        res = [-1 for _ in range(n)]
        stack = []
        for i in range(n*2 -1, -1, -1):
            while(stack and stack[-1] <= nums[i%n]):
                stack.pop()
            res[i%n] = stack[-1] if stack else -1
            stack.append(nums[i%n])
        return res

Leetcode 739  每日温度

请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

这个问题本质上也是找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多少，而是问你当前距离 Next Greater Number 的距离而已。

使用暴力解的话，代码大致如下：

def dailyTemperatures(self, T: List[int]) -> List[int]:
    length = len(T)
    ans = [0] * length
    for i in range(length):
        for j in range(i+1, length):
            if T[i] < T[j]:
                ans[i] = j - i
                break

    return ans

由于存在相同的元素散列表+单调栈的做法报废。因此只有，单调栈+逆序的做法。

class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]:
        length = len(T)

        ans = [0] * length

        # 这里借助列表实现
        # 列表末尾元素即是栈顶元素
        stack = []

        # 从右边往左边开始遍历
        for i in range(length - 1, -1, -1):
            # 如果当前元素大于栈顶元素时，进行出栈
            # 直至当前元素不再大于栈顶元素
            while stack and T[i] >= T[stack[-1]]:
                stack.pop()

            # 这个时候栈顶元素其实就是当前元素右边第一个比其大的元素，先计算距离，然后入栈
            if stack and T[i] < T[stack[-1]]:
                ans[i] = stack[-1] - i

            # 栈为空的情况下，将当前元素入栈
            stack.append(i)

        return ans

❝

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

❞

Reference