单调栈,栈还能单调一下?
之前遇到一个算法题目,自己只会用时间复杂度 O(N^2) 暴力解法解决,有大佬说用单调栈,可以做到 O(N) 的时间复杂度,当时我的表情是这样的:

啥是单调栈?怎么用呢?我就深入学习了一番,于是就有了下文。
什么是单调栈
单调栈,首先是一个栈,满足先进后出的特性,其次是出栈有点特殊:
遇到一个新元素,如果它比栈顶元素小,那就让它入栈,否则就弹出栈顶元素,直到这个新元素比栈顶元素小,再让它入栈。这样的话,最终的结果就是栈内的元素是从栈底到栈顶是递减的,其出栈的顺序就是递增的,这样的栈叫做单调递增栈。
反过来就是单调递减栈。
听起来很容易理解,真正实战的时候,还是有点烧脑。
单调栈的套路
比如说这样一道题目:
给一个数组,返回一个大小相同的数组。返回的数组的第 i 个位置的值应当是,对于原数组中的第 i 个元素,至少往右走多少步,才能遇到一个比自己大的元素,如果之后没有比自己大的元素,或者已经是最后一个元素,则在返回数组的对应位置放上 -1。
例如:
输入 [5,3,1,2,4]
输出 [-1 3 1 1 -1]
解释:对于数字 5,之后没有比它更大的数字,因此是 -1,对于数字 3,需要走 3 步才能达到 4,对于 1 和 2,都只需要走 1 步,就可以遇到比自己大的元素。对于最后一个数字 4,因为之后没有更多的元素,所以是 -1。
你可以把这个当作面试题。
一看这个题目,我相信你第一眼肯定会想到暴力解法:针对每一个要计算的数 a,往后遍历,并计数 cnt,找到第一个比 a 大的就将 cnt 填进去,找不到就填 -1。时间复杂度 O(N^2)。
你能否用时间复杂度 O(N) 的方法解呢?
这就需要使用单调栈了。通过单调递增栈的定义,每当遇到元素大于栈顶元素时,我们就遇到了一个"大数"。这个"大数"比它之前多少个数大我们不知道,但是至少比当前栈顶所对应的数大。我们弹出栈内所有对应数比这个数小的栈内元素,并更新它们在返回数组中对应位置的值。因为这个栈本身的单调性,当栈顶元素所对应的数比这个元素大的时候,我们可以保证,栈内所有元素都比这个元素大。对于每一个元素,当它出栈的时候,说明它遇到了第一个比自己大的元素,这样下来,不难理解这个思路:
for 元素 in 列表:
while 栈不为空 and 栈顶元素 < 元素:
x = 出栈
找到了第一个比 x 大的元素,更新下标
入栈
翻译成代码就是:
input = [5,3,1,2,4]
def find_first_greater(input: list) -> list:
# ans 保存结果,初始化为 -1
ans = [-1] * len(input)
# 模拟递增栈,存放元素的下标,为了计算距离
stack = []
for index, num in enumerate(input):
while stack and input[stack[-1]] < num:
x = stack.pop()
ans[x] = index - x
stack.append(index)
return ans
print(find_first_greater(input))
# output [-1, 3, 1, 1, -1]
有同学会问了,for 循环 + while 循环,这时间复杂度不还是 O(N^2) 吗?其实不然,虽然有 while 循环,但是从整体来看共有 n 个元素,每个元素都被 push 入栈了一次,而最多会被 pop 一次,没有任何冗余操作。所以总的计算规模是和元素规模 n 成正比的,也就是 O(n) 的复杂度。
做的多了,就可以总结出这样的套路:
for 元素 in 列表:
while 栈不为空 and 栈顶元素(大于或者小于)目标值:
出栈
根据业务处理
入栈
单调栈主要解决以下问题:
寻找下一个更大元素 寻找前一个更大元素 寻找下一个更小元素 寻找前一个更小元素 qualified 的 窗口的 max/min sliding window max/min
实战
1、循环数组找最大元素
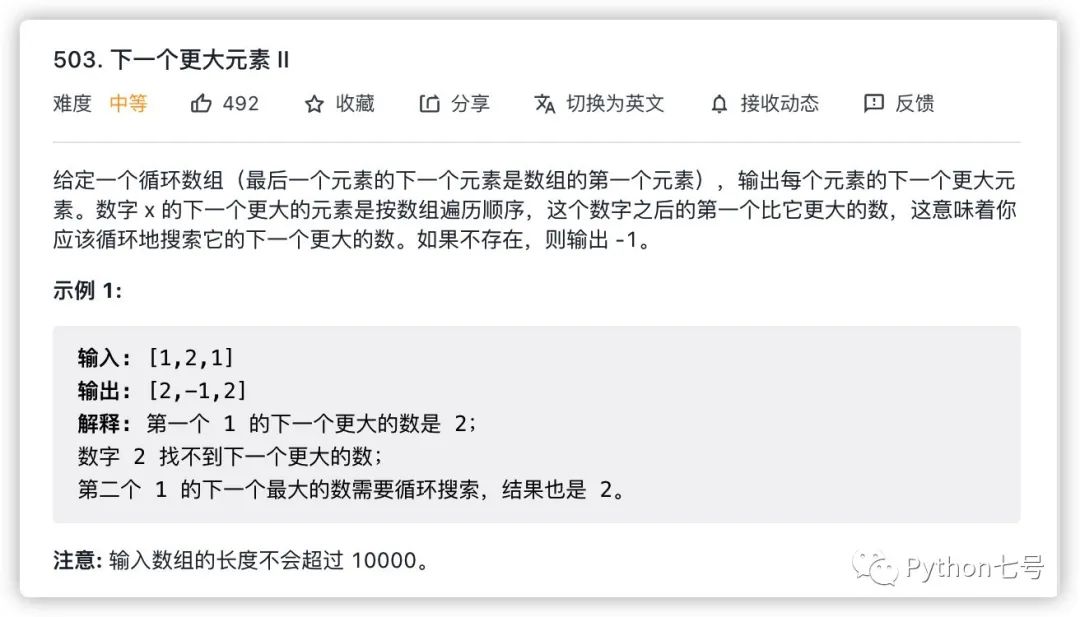
解法:
# coding: utf-8
class Solution(object):
def nextGreaterElements(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
if not nums:
return list()
# 因为是循环数组,这里直接采用扩容的方式,当然也可以直接通过取模在处理
nums2 = nums * 2
# 单调递增栈:用于找到下一个更大的元素
stack = [(0, nums2[0])]
# 维护元素的下一个更大元素
# 这里采用数组的形式
next_g = [-1] * len(nums2)
for index in range(1, len(nums2)):
num = nums2[index]
while stack and stack[-1][1] < num:
origin_index, _ = stack.pop()
# 通过原元素的索引来保存下一个更大元素
next_g[origin_index] = num
# 将原元素的索引保存下来
stack.append((index, num))
return next_g[:len(nums)]
2、接雨水
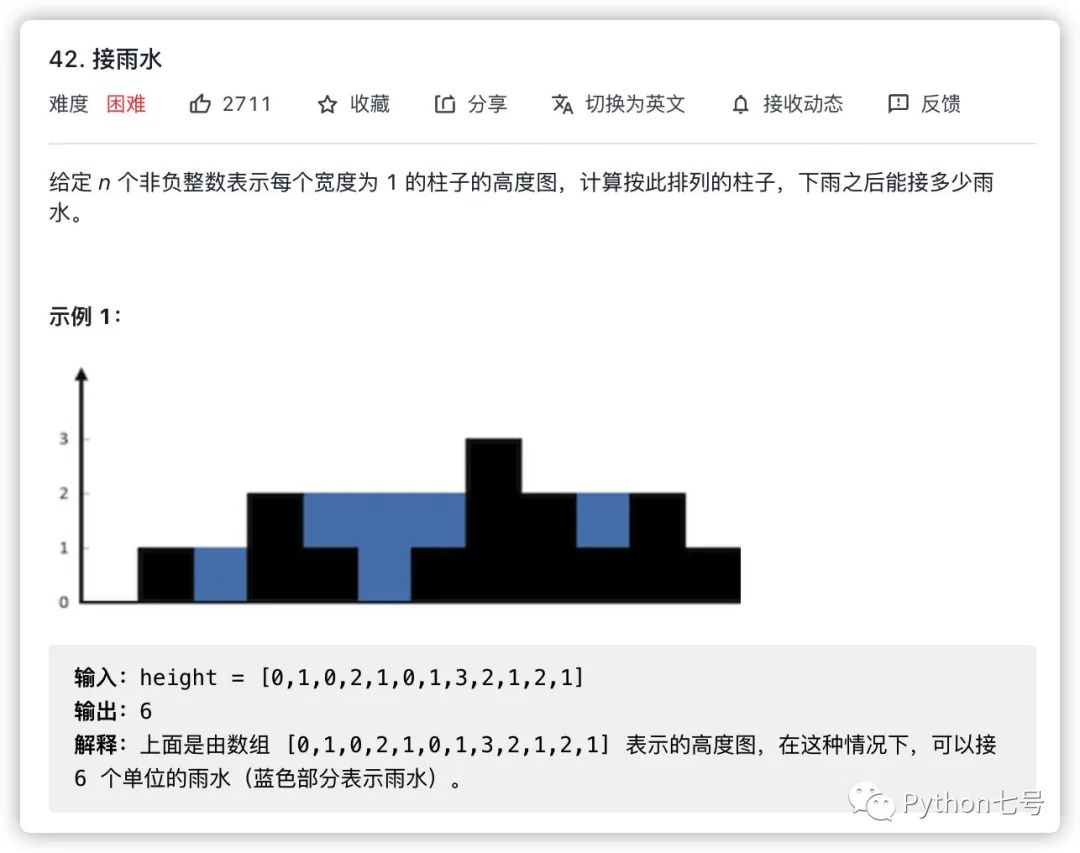
解法:
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
if not height:
return 0
# 单调递减栈
stack = list()
rst = 0
for index in range(len(height)):
h = height[index]
# 只要找到一个比栈顶元素大的元素, 说明有可能形成了一个凹型
while stack and height[stack[-1]] < h:
# 凹型的右边
right_slide = stack.pop()
if stack:
# 栈里面还存在元素,说明形成了一个凹型,可以计算一个容量了:最低的高度 * 宽
rst += (min(height[stack[-1]], h) - height[
right_slide]) * (index - stack[-1] - 1)
stack.append(index)
return rst
3、股票价格跨度
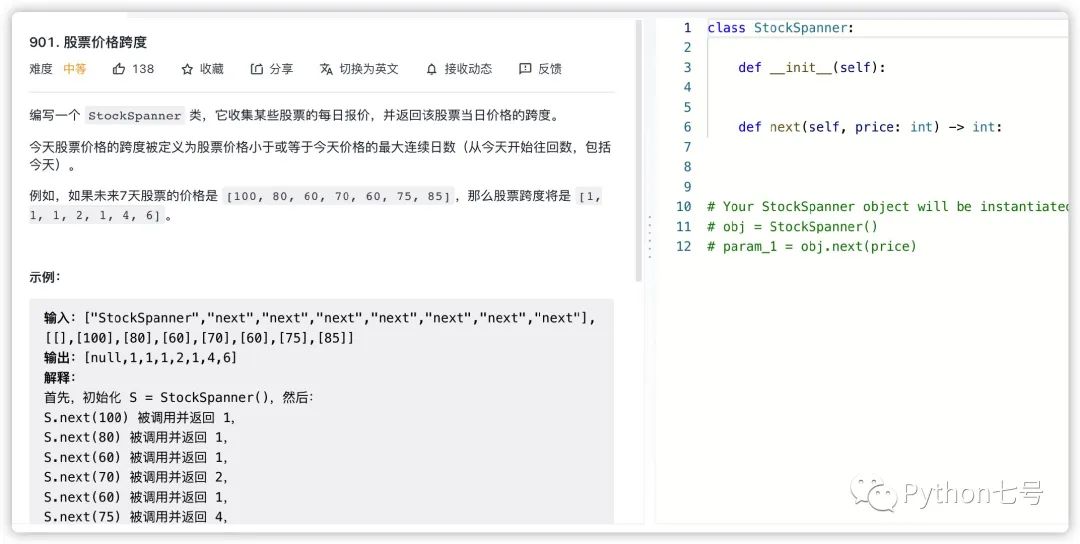
解法:
class StockSpanner(object):
def __init__(self):
# 单调递减栈:存放元素及其跨度
self.prices = list()
def next(self, price):
"""
:type price: int
:rtype: int
"""
rst = 1
while self.prices and self.prices[-1][1] <= price:
# 找到了一个递增对,将其出栈(因为其历史跨度已经记录在了下一个元素中),并将其跨度叠加
rst += self.prices.pop()[0]
# 保持元素及其跨度,便于下一次直接计算历史跨度
self.prices.append((rst, price))
return rst
最后
单调栈是一种理解起来很容易,但是运用起来并不那么简单的数据结构。如果遇到的问题,和前后元素之间的大小关系有关系的话,可以尝试使用单调栈,也有不少问题需要先转换为求下一个最大/小元素的问题,然后再使用单调栈解决。本文分享了单调栈的定义,套路,典型实战案例,如果有帮助,请点赞、在看、关注支持,这次一定。
关注「Python七号」每天学习一个小技术
