栈栈栈栈栈栈栈栈栈栈栈栈栈栈栈栈栈栈-技术圈

大家好，我是沉默王二。

今天周一，又是 3 月份的第一天，所以今天必须来点硬核的内容。

上次给大家图解了霍夫曼编码，有同学说每天早上都会看一篇二哥的文章，但因为这一篇星标了；还有做律师的同学乱入，表示虽然看不懂，但感觉很厉害；当然了，更多的同学对文中提到的知识点进行了思考，有些得出了自己的结论，有些没有，但不管有没有结论，重要的是主动去思考，也只有这样，才能收获更多！

还有很多同学直呼内行，强烈要求我多更一些这方面的文章，于是就有了今天这篇——栈（stack）。有些地方喜欢称呼它为堆栈，我就很不喜欢，很容易和 heap（堆）搞混，尤其是对于新手来说，简直就是虐心。

栈是一种非常有用的数据结构，它就像一摞盘子，第一个放在最下面，第二个放在第一个上面，第三个放在第二个上面，最后一个放在最上面。

对于这一摞盘子，我们可以做两件事情：

在最上面放一个新盘子
把顶部的盘子拿走

这两件事情做起来很容易，但如果从中间或者底部抽出来一个盘子，就很难办到。如果我们想要拿到最下面的盘子，就必须把它上面的所有盘子都拿走，像这样的一个操作，我们称之为后进先出，也就是“Last In First Out”（简称LIFO）——最后的一个进的，最先出去。

对于栈这样一个数据结构来说，它有两个常见的动作：

push，中文释义有很多种，我个人更喜欢叫它“压入”，非常形象。当我们要把一个元素放入栈的顶部，这个动作就叫做 push。
pop，同样的，我个人更喜欢叫它“弹出”，带有很强烈的动画效果，有没有？当我们要从栈中移除一个元素时，这个动作就叫做 pop。

对于上面这幅图来说，3 这个元素最先放进去，却是最先被移除的——遵循 LIFO 的原则。

明白了栈的基本操作后，我们需要去深入地思考一下，栈是如何工作的。换句话说，为了使栈这个数据结构按照栈的方式去工作，它需要什么？

1）栈需要有一个指针，我们称之为 TOP，用它来指向栈中最顶部的那个元素。

2）当我们初始化一个栈的时候，我们把 TOP 的值设置为 -1，这样我们就可以通过 TOP == -1 来判断栈是否为空。

3）当我们要在栈中压入一个元素的时候，我们把 TOP 的值加 1，然后把新压入的元素指向 TOP。

4）当我们要从栈中弹出一个元素的时候，我们把 TOP 的值减 1，然后把保持在最顶部的那个元素指向 TOP。

5）当我们压入一个元素的时候，需要检查栈是否已经满了。也就是说，需要有一个 isFull() 的方法来判断。

6）当我们要弹出一个元素的时候，需要检查栈是否已经空了。也就是说，需要有一个 isEmpty() 的方法来判断。

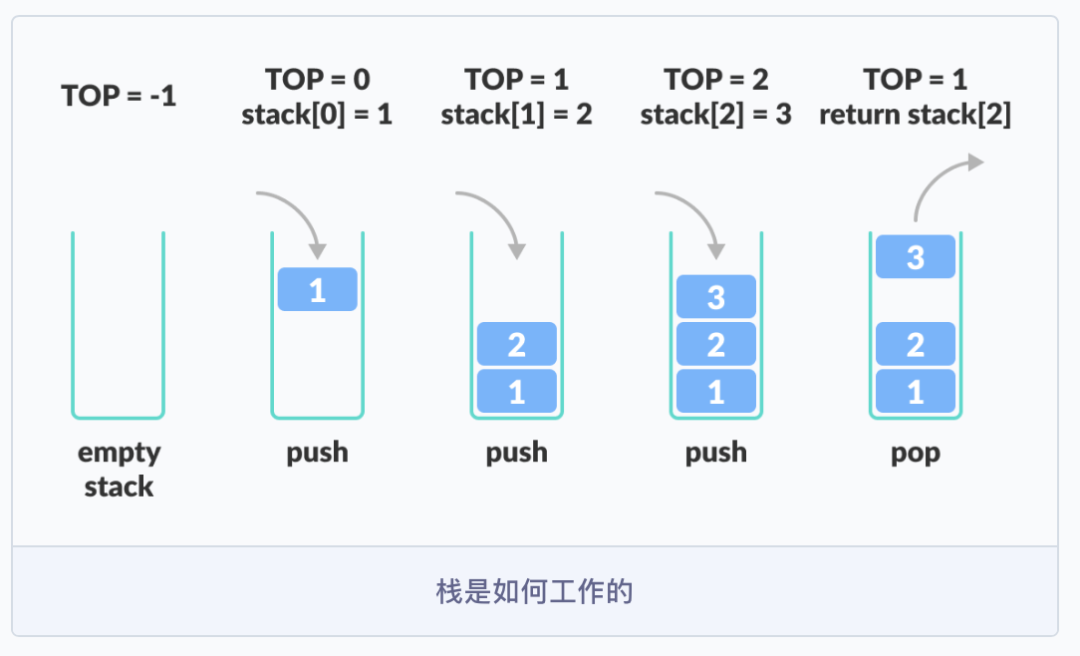
空栈的时候，TOP 等于 -1；把元素 1 压入栈中的时候，stack[0] 为 1，TOP 加 1 变为 0；把元素 2 压入栈中的时候，stack[1] 为 2，TOP 加 1 变为 1；把元素 3 压入栈中的时候，stack[2] 为 3，TOP 加 1 变为 2；把元素 3 从栈中弹出后，返回元素 stack[2]，TOP 减 1 变为 1。

假设栈中的元素是 int 类型，我们可以用 Java 语言来自定义一个最简单的栈。它需要 3 个字段：

int arr[]，一个 int 类型的数组，来存放数据
int top，一个 int 类型的标记
int capacity，一个 int 类型的容量

class Stack {
    private int arr[];
    private int top;
    private int capacity;
}

初始化栈：

Stack(int size) {
    arr = new int[size];
    capacity = size;
    top = -1;
}

往栈中压入元素：

public void push(int x) {
    if (isFull()) {
        System.out.println("溢出\n程序终止\n");
        System.exit(1);
    }

    System.out.println("压入 " + x);
    arr[++top] = x;
}

从栈中弹出元素：

public int pop() {
    if (isEmpty()) {
        System.out.println("栈是空的");
        System.exit(1);
    }
    return arr[top--];
}

返回栈的大小：

public int size() {
    return top + 1;
}

检查栈是否为空：

public Boolean isEmpty() {
    return top == -1;
}

检查栈是否已经满了：

public Boolean isFull() {
    return top == capacity - 1;
}

来个 main() 方法直接测试下：

public void printStack() {
    for (int i = 0; i <= top; i++) {
        System.out.println(arr[i]);
    }
}

public static void main(String[] args) {
    Stack stack = new Stack(5);

    stack.push(1);
    stack.push(2);
    stack.push(3);
    stack.push(4);

    stack.pop();
    System.out.println("\n弹出元素后");

    stack.printStack();
}

打印结果如下所示：

压入 1
压入 2
压入 3
压入 4

弹出元素后
1
2
3

由于我们是通过数组来实现的栈，所以 push 和 pop 的时间复杂度就是 O(1)。

尽管栈是一种非常简单的数据结构，通过上面的代码大家应该也能感受得出来，轻而易举地就实现了，但是栈却是一种非常强有力的数据结构，可以在很多场景中使用，比如说：

1）反转一串字符：由于栈是 LIFO 的，所以反转一串字符很容易，按照正常的顺序把字符压入栈中，然后再弹出来就行了。

2）用于计算器：记得我实习的时候，公司就给我们新人安排了我们一个小项目——模仿一个 Win 7 的计算机，用来考察我们是不是真材实料，要想计算一个复杂的表达式，比如说 2 + 5 / 3 * (6 - 2)，就需要一个栈来容纳这些数字和运算符，然后按照优先级弹出后进行计算。

嗯，这个计算要比想象中复杂一些，新手同学可以私底下实现一下，不仅能够提高对栈这种数据结构的理解，还能对运算符的一个优先级进行思考。

很显然，栈，给我赢得了一次实习的机会，避免了被刷下去的危机。

3）用于浏览器：浏览器的后退按钮会把我们访问的 URL 压入一个栈中，每次我们访问一个新的页面，新的 URL 就压入了栈的顶部，当我们点了后退按钮，最新的那个 URL 就从栈中移除，之前的那个 URL 就被访问到了。

好了，下课，今天的栈就到此为止吧。

多 BB 一句。上次，很多好心的同学为了使我吃上香喷喷的辣条，硬是不想学会霍夫曼编码，结果我真吃了——结果的结果——脸上长痘痘了，我想说的是，同学，能不能不要这么贴心，这次学会学不会我都不吃了，哼。