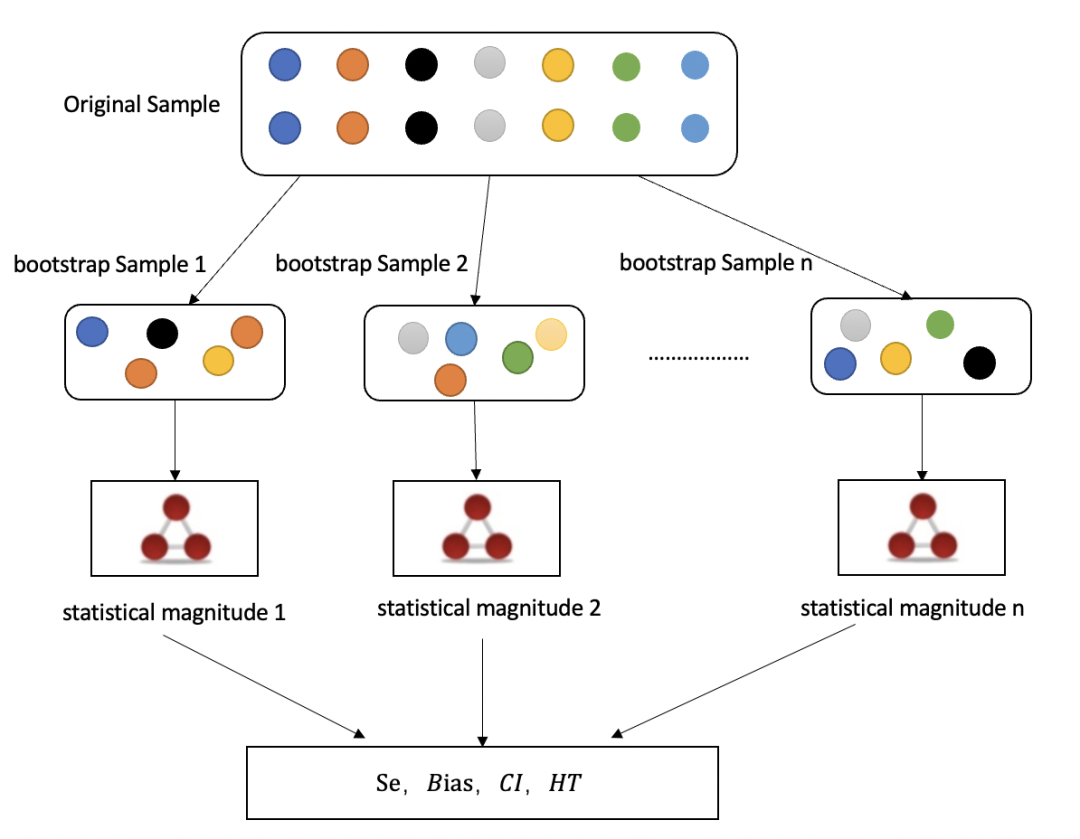
▐ 前言

在【阿里妈妈数据科学系列】前三期内容中，我们粗略的介绍了AB TEST 基础知识与框架，本期开始将着重细化介绍 AB TEST 每一个部分具体的方法论与技术，包括实验设计、实验数据分析、实验中常见的误区等。本期我们将介绍 Bootstrap 方法在实验统计推断中的应用。在实际的场景下，统计推断是 AB TEST 不可或缺的一部分，一次实验的结论是否真的显著，均需要通过统计推断的方法进行证明，否则我们无法判断实验效果是否来自实验因素或者随机扰动。如我们前几期里提到过的，常见的实验统计推断方法来自假设检验理论，我们通过大数定律以及假设检验理论结合，以实验组和对照组的数据构造一个假设检验流程，具体细节可以参照此前的文章。但是在实际的应用中，我们可能会遇到如下的问题：

实验样本量太小，即便可能存在效应也无法有效的检验出显著的效果
检验指标构造复杂，如两随机变量的商构造的指标，例如CTR=CLICK/PV，此处PV、CLICK均为随机变量，在计算CTR的方差时，需要采用不同的计算方法来近似计算方差。
样本数据倾斜严重，头部效应明显，个别样本会严重影响整体效果的差异。

面临上述问题是，常规的统计推断方法也有一定的解决方案，但是会更复杂，而且需要 case by case 的分析，此时 Bootstarp 的方法能够很好的解决上述的问题。

▐ 基本思想

Where there is sample, there is uncertainty。

英语 Bootstrap 的意思是靴带，来自短语：“pull oneself up by one′s bootstrap”，18世纪德国文学家拉斯伯（Rudolf Erich Raspe）的小说《巴龙历险记（或译为终极天将）》（Adventures of Baron Munchausen) 记述道：“巴龙掉到湖里沉到湖底，在他绝望的时候，他用自己靴子上的带子把自己拉了上来。”现意指不借助别人的力量，凭自己的努力，终于获得成功。在这里“bootstrap”法是指用原样本自身的数据抽样得出新的样本及统计量，根据其意现在普遍将其译为“自助法”。

简单的说，Boostrap 的底层逻辑是 Resample（重抽样），既然我们只知道这些数据，那么我们就把这些数据看做整体（Empirical dist.），基于这些数据再进行多次抽样并计算得我们想要的内容（更加充分运用了这些数据）。此外：我们也把 MC in Statistic Inference 中的方法叫做参数 Bootstrap（因为它也涉及到了重新的多次抽样，不过是从 population 中抽取的），而这里的方法则叫做非参数 Bootstrap，我们一般讲的 Bootstrap 就是这里的。

在实验中我们采用非参数的 Bootstrap 方法，其核心思想和基本步骤如下：

（1）假设原始样本数量为 N,通过 resample 从原始样本中抽取N个样本，此过程允许重复抽样；

（2）根据抽出的样本计算给定的统计量T；

（3）重复上述B次（一般大于1000），得到B个统计量T；

（4）计算上述B个统计量T的估计量，如均值、方差等，得到原样本的均值与方差等统计量。

应该说 Bootstrap 是现代统计学较为流行的一种统计方法。通过对给定数据集进行有放回的重抽样以创建多个数据子集，生成统计量的经验分布，可以计算标准误差、构建置信区间并对多种类型的样本统计信息进行假设检验,其应用范围逐步扩大，是目前业界对工业化 ABTEST 实验效果常见的处理方法。

▐ 简单的推导过程

用 Bootstrap 来计算估计量的 SE, BIAS

前面讲过，Bootstrap 就是多次抽样，这样就得到了 Empirical dist. ，而我们的估计量则是。我们先来看SE，考虑

我们使用 "Plug-in" Priniciple，则

其中的为 B 个 Bootstrap 估计量的均值；分母用了B-1是为了无偏。于是我们得到了SE的 Bootstrap 估计公式

对于BIAS

用 Bootstrap 来计算估计量的 CI

我们主要介绍3种常用的 Bootstrap 计算 CI 的方法。

标准 Bootstrap（SB）

标准 Bootstrap 方法计算CI是以bootstrap计算的出的样本均值、样本方差构造的标准 CI 的计算方法，我们可以通过 Bootstrap 计算样本均值与方差

在标准化之后，n 很大的情况下由 Central Limit Theorem 可知近似标准正态分布，在统计量无偏以 se 代替 std 的条件下，我们就可以得到一个θ的置信区间

百分位数 Bootstrap（PB）

百分位数的 Bootstrap 直接用的分布来估计，我们通过 Bootstrap 构造了一个的分布，则实际的区间估计可以用的分位数直接进行估计，的置信区间为：

t百分位数Bootstrap（PTB)

t 百分位数 Bootstrap 是对 SB、PB 的一种融合，后者对分布要求过高，（1 无偏；2 近似正态），通常可以得到比百分位数 Bootstrap 更加精确的 CI，类似标准标准 Bootstrap 我们构造一个统计量，不过此处构造的是 t-type 统计量

此时，我们对于每一个 Bootstrap 样本估计，相当于对t统计量进行修正，采用百分位的计算方式计算对应的t分布分位点，则通过该方式构造的的置信区间为

显然 PTB 是更好的计算 CI 的方法，其收敛性也更好，在实际应用中，可以根据实际计算的复杂度，选取合适的计算方法。

结果比较

此处，取实际生产中小样本某实验结果，可见以上三种方法置信区间的收敛性均好于常规的统计方法。

	常规方法	SB	PB	PTB
置信区间	[1477,1503]	[1479,1502]	[1479,1502]	[1480,1502]
宽度	26	23	23	22

▐ 应用实例

因为 Bootstrap 在小样本场景下效果显著，在大流量场景效果和基于常规方法的推导无明显差异，因此Bootstrap 更多的应用在阿里妈妈BP侧的类实验场景下，我们以一个简单的例子梳理一下 Bootstrap 方法的应用流程，考虑如下场景，我们需要对某个BP侧新增产品功能进行验证，证明该功能是否对 CTR 有促进作用，因此我们基于类实验的策略，抽取了实验组VS对照组各1万客户进行实验，收集实验数据格式如下（数据随机生成，并非实际生产数据）。

依照上述的计算逻辑，我们来估计，对该数据进行 resample 过程，每次抽取20000个样本，共抽取1000次（1000次后数据相对较为稳定），则对于1000个 Bootstrap 样本集合我们可以计算1000个，其中

则

采用PB算法估计的置信区间，将1000个升序排列，取2.5%，97.5%分位数，可得95%置信区间为。

通过置信区间与0的比较，我们能够看到该指标并没有显著提升。基于以上的流程我们可以对任意指标通过 Bootstrap 方式构造置信区间，证明该指标是否有显著变化。

▐ Bootstrap&Jackknife

通常在提到 Bootstrap 时，也会提到 Jackknife 作为比较，Jackknife 方法由 Quenouille(1949) 提出，并由 Tukey(1958) 创造了 Jackknife 这一术语。Jackknife 采用的 leave-one-out 的思想，对于样本容量为n的集合，采样 n 次，每次无放回采样 n-1 次，以此来估计样本的估计量。具体推到方式此处不作赘述。

Jackknife 通常可以看做 Bootstrap 的一种特例，同样是 resample 的过程，主要的区别在于：

抽样方法不同。Bootstrap 采用的是「有放回抽样」，jackknife采用的是「无放回抽样」。
Jackknife 在解决不光滑 (Smooth) 参数估计时会失效，而 Bootstrap 可以解决这个问题，例如中位数，分位数等估计量。
若统计量是线性的，二者的结果会非常接近。虽然从表面上看，Jackknife 似乎只利用了非常有限的样本信息。对于非线性统计量而言，Jackknife 会有信息损失，此时 Bootstrap 较好。这是因为，Jackknife 可以视为 Bootstrap 的线性近似。换言之，Jackknife 的准确程度取决于统计量与其线性展开的接近程度。

▐ 总结

虽然 Bootstrap 很早就被提出，但是受限于计算能力的约束，并没有被大幅应用，伴随着计算机算力的提升 Bootstrap 重新崛起，成为当前非参数估计中最实用的方法之一，在 AB TEST 中更是解决小样本、缩减方差、简化计算的利器，同时结合不同的算法 DID、bayes 估计等，Bootstrap 仍然有很大的发挥空间。