详解AB Test分析-技术圈

一、背景

实际业务场景中，为了优化产品体验，我们常会提出多种产品策略方案。比如，手机的温控策略，可能会有多种方案，但选择哪种方案能给用户带来更好的体验呢？除了通过实验室测试、招募试用用户体验和使用现有数据验证等方法之外，最直接的方法是AB Test。AB Test是一种测试方法，通过对比两种策略在研究主体上的反应，判断哪种策略更优。

虽然AB Test定义简单，但使用不当，反而会产出错误的结论，本篇文章旨在帮助我们科学使用AB Test。

二、ABTest流程

我总结AB Test的主要流程如下：

1. 沟通测试需求

2. 讨论观测指标

3. 选择投放目标

4. 配置实验策略

5. 评估数据结果

1. 沟通测试需求

当业务方提出使用AB Test去测试策略效果，我们要先问一个问题：“我们真的需要AB Test吗？”。AB Test整个流程耗时，而且可能会影响用户，特别是一些用户感知强的功能策略。如果有其它策略评估手段，建议先考虑它们，真的有必要，再考虑使用AB Test。

2. 讨论观测指标

我们要测试不同策略，那么最后我们要观测什么指标呢？这个指标一定能很好地反映策略效果，例如更换网页广告展示策略，我们除了监控跳转率，也能加入转换率等指标。好的策略评估往往需要监控多个观测指标，同时，观测指标的制定需要与业务方讨论，避免单方输入。特别要注意，指标应考虑多个业务场景的影响，比如说推性能策略AB测试，不应该只关注性能指标，也要关注用户使用产品时的行为指标。

3. 选择投放目标

我们在测试前，需要圈取策略投放目标范围，这个投放目标涉及软硬件版本、用户群、平台等。不合理的投放会造成最后测试结果不具有参考价值，举些错误例子[1]：

轮流在不同版本上线测试：在不同硬件/软件版本上，上线不同的策略，最后AB test引入版本差异可能不太明智。举例，在旧版本和新版本上分别上线温控策略A和B，但新版本补丁更新后，手机可能会带来温度改善，那这样就很难对比数据知道，手机温度的改善究竟是温控策略还是版本更新所致。类似地，轮流在不同时间上线测试也是不太可取的。
选择存在明显特征差异的用户分发策略：在选取对照组和实验组时，没有考虑分发群体的特征差异。举例，我要分发温控策略，对照组是广东用户，实验组是黑龙江用户，不同省份的环境温度本身存在差异，导致两拨用户的手机发热情况也不一致，所以在策略效果上不具有可比性。

正确选择投放目标，主要关注两个方面：

(1) 投放量

(2) 投放人群

(1) 投放量

投放量很重要，如果少了，会担心观测指标会受偶然因素影响，投放过多，又担心测试风险变大，造成市场反响不好。现在网络上已存在很多AB Test样本量计算器，如图1所示：

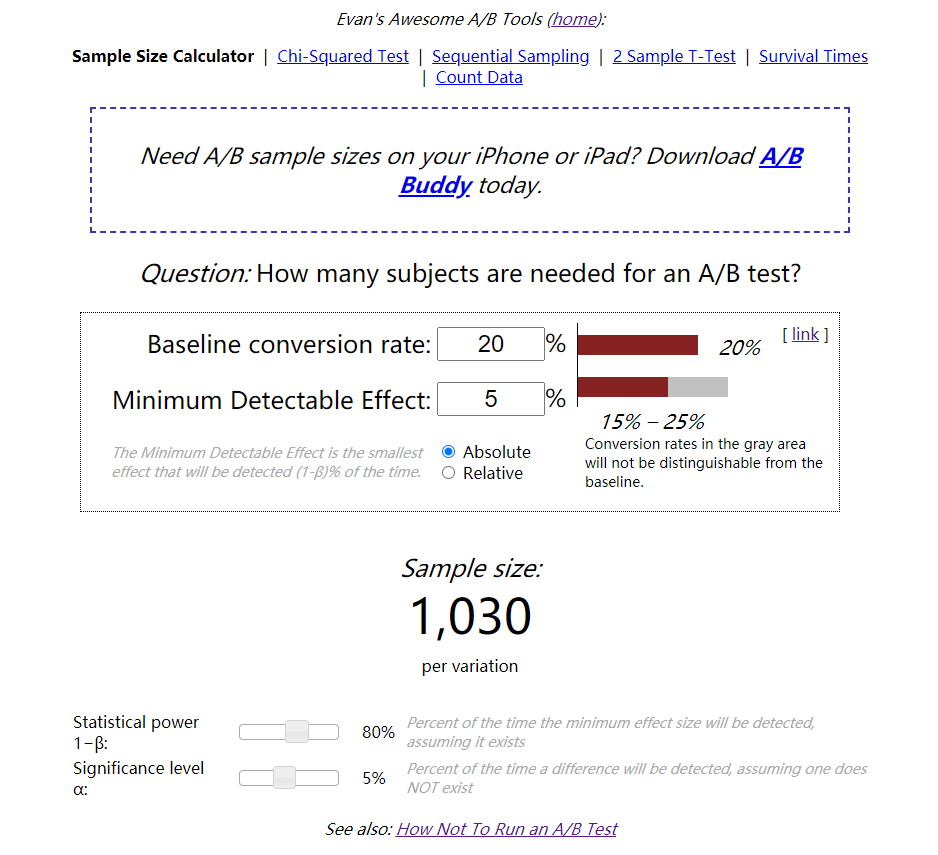
图1: AB Test样本量计算器[2]

实际AB Test应用中，我们用的观测目标多是比例形式(例如: 转换率、留存率等)。在统计学中，有一个叫做两样本比例假设验证，该验证的最小样本量计算公式如下[3]:

$n=\frac{(Z_{\alpha/2}\sqrt{2p_1 (1-p_1)}+Z_{\beta}\sqrt{p_1(1-p_1)+p_2(1-p_2)})^2}{|p_2-p_1|^2}$ 参数解释:

$n$ : AB Test的最小样本量。
$Z$ : $Z$ 分位数(Z Score)，某 $x$ 值到均值的距离（可正可负）是多少个标准差，即 $Z=\frac{x-\mu }{\sigma }$ ，可查表获取。
$p_1$ : 基准比例 (Baseline Rate)。若历史大盘数据的广告转换率是20%，则 $p_1=0.2$ 。
$p_2$ : 期望比例 (Expect Rate)， $p_2$ = $p_1$ + 最小可检测影响 (Absolute Minimum Detectable Effect)，如果我们希望转换率指标提高5%，且低于5%的差异对产品影响不大，则Minimum Detectable Effect设为5%。
$\alpha$ : 第一类 (Type I error) 错误概率上限，也称Significance Level。
$\beta$ : 第二类 (Type II error) 错误概率上限，Statisical Power = $1 - \beta$ 。

我们来深入了解下 $\alpha$ 和 $\beta$ ，假设我们要对比策略A和策略B的观测指标，我们会建立假设H0: A和B两组不存在本质差异，H1: A和B两组存在差异。针对假设，我们会有如下矩阵：

图2: AB Test假设的概率矩阵

由图2，我们可以知道：

Type I error ( $\alpha$ )：真实AB没区别，但是我们却认为有区别。
Type II error ( $\beta$ )：真实AB有区别，但是我们却认为没有区别。

一般来说， $\alpha$ =5%， $\beta$ =20%。现实应用中，如果出现Type II error，我们会选择持续优化实验方案，但往往Type I error是更困扰人的，因为AB没区别，我们还误认有区别，最后错误认为新策略有用就推广到全量用户，这是不好的，因此 $\alpha$ 常会设置小于 $\beta$ 。[4]

说了那么多，我们举个实际案例：假设我们现在大盘用户采用广告策略A，广告转换率是20% ( $p_1$ )，而我们有个新策略B想测试，我们预估它能带来广告转换率提高5% (Minimum Detectable Effect) ，那我们最少需要多少样本量？样本量是1030个，请见图1，计算过程如下:

- $p_1$ = 20%

- $p_2$ = $p_1$ + Minimum Detectable Effect = 20% + 5% = 25%

- $\alpha$ = 5%

- $\beta$ = 20%

- $Z_{\alpha/2}$ = $Z_{5\%/2}$ = -1.959963985

- $Z_{\beta}$ = $Z_{20\%}$ = -0.841621234

$n=\frac{((-1.959963985)*\sqrt{2*0.2*(1-0.2)}+(-0.84162134)*\sqrt{0.2*(1-0.2)+0.25(1-0.25)})^2}{|0.25-0.2|^2}=1030.219$

(2) 投放人群

在AB Test中，投放人群=流量，选择投放人群有两种形式：

随机: 随机从大盘用户里抽样。例如userid单双尾号抽取、随机种子打乱数据再抽样等。
定向: 针对特定用户群体下发策略。例如结合用户画像标签或自定义规则筛选用户。

以上两种形式均要保证策略AB下两组用户相似。

4. 配置实验策略

在企业真实环境中，会有很多AB Test实验，我们需要先判断不同实验之间关系:

(1) 正交实验: 实验之间相互不影响。举例: AB Test1是测试不同按钮颜色的实验，AB Test2是测试不同广告算法的实验，Test1的按钮颜色不会影响Test2广告算法的效果，所以Test1和2之间是正交实验，

(2) 互斥实验: 实验之间存在相互影响。举例: AB Test1是测试温控限频策略对温度的影响，AB Test2是测试温控降亮度对温度的影响，Test1和Test2都会影响温度，所以Test1和2之间互斥。

我们都知道，全局流量基本是固定的大小，不可能说划分的每个流量群体在同一时刻只开展一个实验，不然容易发生流量饥饿。为此，Google在2010年提出了多层重叠实验架构 (Overlapping Experiment Infrastructure) [5] :

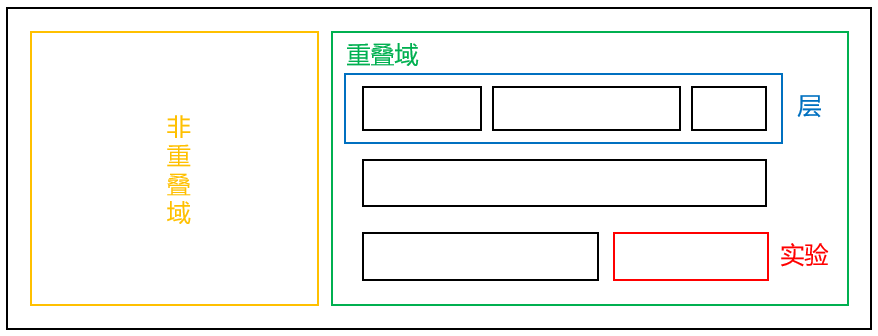
图3: Google的多层重叠实验框架

该框架有三个组成成分：

域 (Domain): 流量的一个划分，非重复域指的是不同AB Test共享测试在同一流量上，重复域则存在细分流量的可能。
层 (Layer): 系统参数的子集 (域包含层，层也能包含域)。
实验 (Experiment): 可以看作一个AB Test实验。

当我们要做正交实验的时候，可以考虑设计重叠域，案例如下：

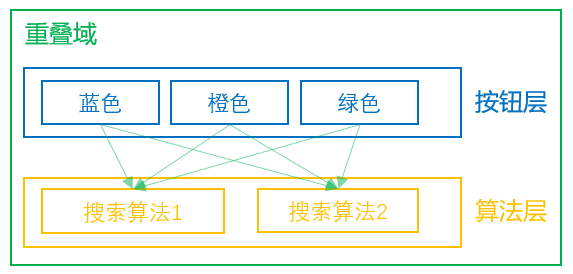
图4: 正交实验案例

比如我们在做网页的ABtest，我们先建立一个有一定流量规模的域，然后对流量划分为3份，用作测试按钮颜色，同样，我们也可以对流量划分2份，用于不同搜索算法的测试。按钮层和算法层互不影响，共享使用相同流量。

而当我们要做互斥实验时，则可以考虑在非重叠域或单层里实验，案例如下：

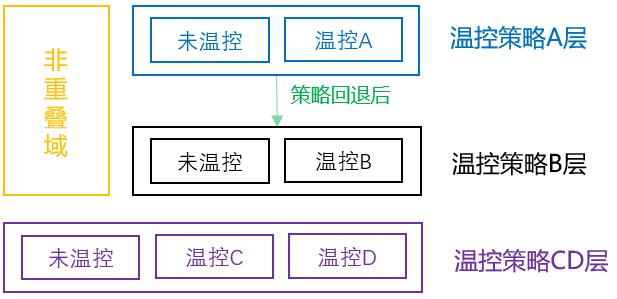
图5: 互斥实验案例

如果我们现有要测试不同的温控策略，分业务场景有以下方案：

若已知或预计未来会有n个互斥实验策略，则可以考虑将对单层流量划分出多个buckets，然后分配给不同的温控策略实验，例如图5的温控策略CD层。
若不确定未来的互斥实验计划，可以考虑先在非重叠域或单层上先实验当前测试，然后若有新的策略要测试时，对原有实验策略回退后再测试新实验，例如图5的非重叠域和温控策略AB层。

简单来说：正交用分层，互斥用分流。

5. 评估数据结果

假设我们有了数据结果，策略A的转换率是10%，策略B的转换率是8%，那我们说策略A比策略B好，这样就可以了吗？不可以，因为可能是抽样误差引起的转换率差异，为了区分实验A和B的差异是由抽样误差引起的？还是本质差别引起的？我们需要做假设验证 (hypothesis testing)。统计学中有很多假设验证方法，例如：

T检验: 也称Student's t test，适用: 样本量较小(如n<30)，总体标准差未知，正态/近似正态分布的样本。目的: 比较平均值之间差异是否显著。
Z检验: 也称U检验，适用: 大样本量(如n>30)，总体标准差已知，正态/近似正态分布的样本。目的: 比较平均值之间差异是否显著。
F检验: 适用: 正态/近似正态分布的变量。目的: 检验两个正态分布变量的总体方差是否相等。
卡方检验: 也称chi-square test或X2 test，适用: 类别型变量。目的: 检验两个变量之间有无关系，例如性别和是否购买数码产品之间的关系。

在ABTest中，我们一般都会用T/Z检验，它们的使用场景如下：

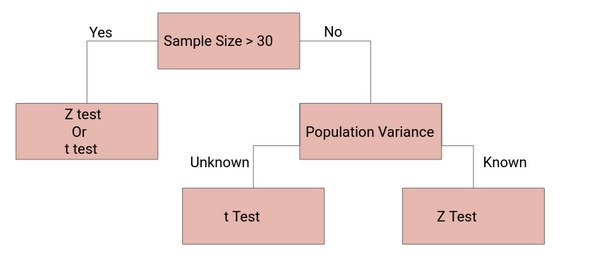
图6: T/Z检验的使用场景 [6]

我们做AB Test，“如果样本量足够大，那么Z检验和t检验将得出相同的结果。对于大样本，样本方差是对总体方差的较好估计，因此即使总体方差未知，我们也可以使用样本方差的Z检验”。[6]，但正常来说，除非是长期的实验(0.5-1年)，例如算法，会选择Z检验。正常的短期AB Test基本是实验1个月内甚至说1-2周，那么此时建议选择T检验。

假设检验步骤如下：

(1) 建立假设

(2) 设置决策标准

(3) 假设检验出结论

(1) 建立假设

假设检验的检验有两种：单边假设检验和双边假设检验，前者判断AB是否显著优/劣于对方，后者判断AB是否存在显著差异。

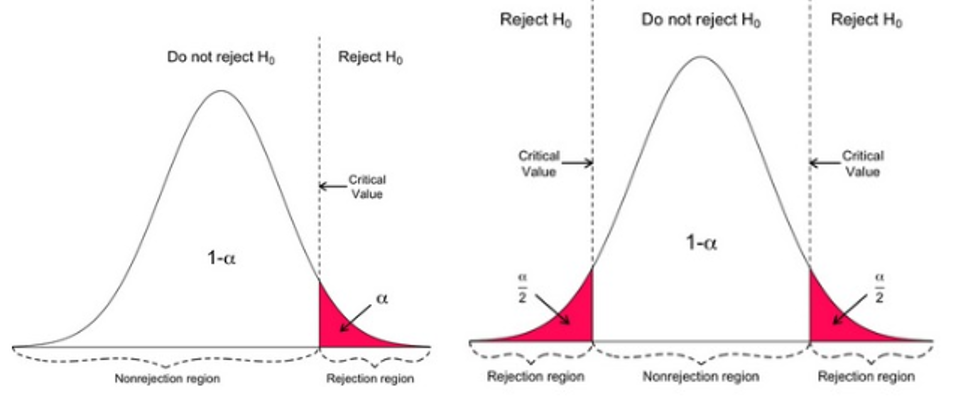
图7: 单边和双边假设检验[6]

以双边检验为例，假设策略A 7天的转换率平均值为 $\mu_1$ ，策略B 7天内转换率平均值为 $\mu_2$ ，则建立假设:

零假设(H0): $\mu_1=\mu_2$ ，即假定策略AB没显著差异。
备择假设(H1): $\mu_ 1\neq\mu_ 2$ ，即策略AB有显著差异。

(2) 设置决策标准

假设检验的决策标准有两种:

p值: p值是用来判定假设检验结果的参数，如果p值很小，说明原假设情况发生的概率很小，我们就有理由拒绝原假设。我们一般会认为显著性水平值(图8的Significance Level $\alpha$ )为0.05，即如果p值<0.05，则有超过95%的信心拒绝零假设。
检验统计值: 例如t值。当我们定了显著性水平后，可以透过查表，得到对应的t临界值，若t真实值(Test Statistic) > t临界值(Critical Value)，我们会拒绝零假设。

注意：t值和p值的假设验证方法是相反的。

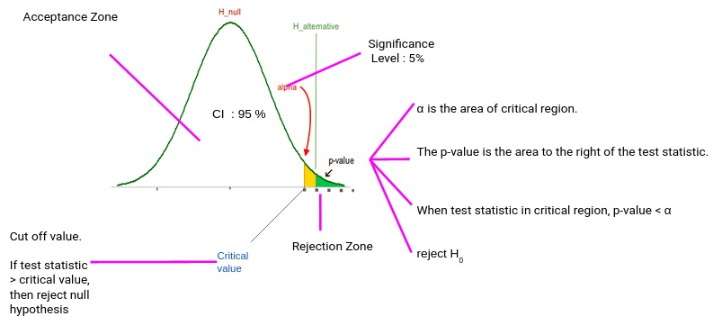
图8：假设检验决策逻辑

(3) 假设验证出结论

我们举个案例做假设验证吧，假设：

策略A 7天的转换率: [64.2, 28.4, 85.3, 83.1, 13.4, 56.8, 44.2]，平均值为53.629，标准差为26.886。
策略B 7天的转换率: [45, 29.5, 32.3, 49.3, 18.3, 34.2, 43.9]，平均值为36.071，标准差为10.745。

由于样本量为7个，所以选择T检验。而T检验在实际应用中有三种[8]:

单样本T检验: 总体样本vs抽样样本。
配对样本T检验: 同一对象接受两种不同的处理。
双独立样本T检验: 两组独立样本。

正常情况下，我们AB Test用的是两组独立样本，控制变量进行对比实验，所以我们这里采用双独立样本T检验[9]:

$t=\frac{\bar{X_1}-\bar{X_2}}{s_p\sqrt{\frac{2}{n}}},\; where\; s_p=\sqrt{\frac{s_{X_1}^{2}+s_{X_2}^{2}}{2}}$ $s_{X_1}^{2}$ 和 $s_{X_2}^{2}$ 是策略A和B的方差， $\bar{X_1}$ 和 $\bar{X_2}$ 则是它们的平均值。

$t=\frac{53.629-36.071}{\sqrt{\frac{{26.886}^{2}+{10.745}^{2}}{7}}}=1.604$ 我可以调用python的scipy.stats.ttest_ind()计算出t值和对应的p值:

pythonfrom scipy.stats import ttest_indn1_samples = [64.2, 28.4, 85.3, 83.1, 13.4, 56.8, 44.2]n2_samples = [45, 29.5, 32.3, 49.3, 18.3, 34.2, 43.9]
# 独立双样本 t 检验的目的在于判断两组样本之间是否有显著差异：# 当我们使用scipy.stats.ttest_ind(x, y)，我们建立的假设是在x.mean()-y.mean()，但常为了得到正值结果，我们常会要求x.mean()>y.mean()。# 即放置顺序是(n1_samples, n2_samples)，而不是(n2_samples, n1_samples)t_val, p = ttest_ind(n1_samples, n2_samples)print('t值：',t_val,"   p值：", p)

代码结果返回: t值：1.6043475026567464 p值：0.13461684984333577。p>0.05，接受原假设，所以最终结论是: 策略A和B之间没有显著差异。

知识点扩展: 除了通过p值验证假设，还可以通过t值，例如我们定了p值为0.05，每组样本内有7天的转换率，则自由度(Degrees of Freedom, df)=size(n1_sample) + size(n2_sample)-2=12)，然后查T表，可知t临界值为2.179，如图9。因为t真实值<2.179，所以我们接受原假设。

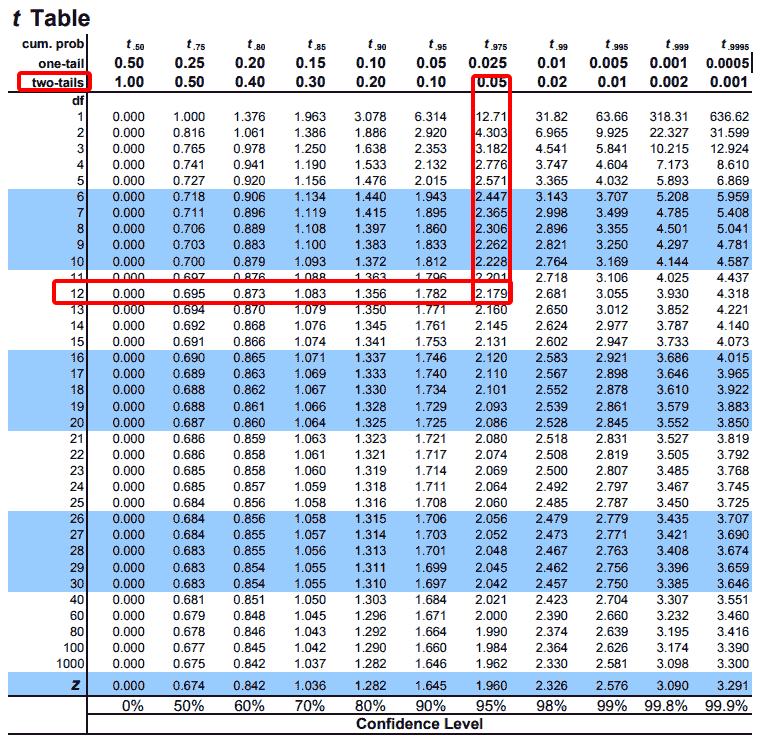
图9: T表[10]

上面讲的是双边检验，如果策略A是旧策略，B是新策略，我们想看是否新策略B比旧策略A好，那需要用到单边检验，此时假设建立为:

H0: A≥B
H1: A<B

单边检验只要把前面scipy.stats.ttest_ind()计算出p值除以2后，再与显著性水平对比即可，这里是p/2=0.1346/2=0.0673>0.05，接受原假设，即新策略B不会比旧策略A显著提升转换率。我们也能从t值着手判断: 由图8可得，单边检验下，t临界值为1.782，t=1.604<1.782，未掉入右侧的拒绝域，所以接受原假设。

参考资料

[1] ABTest - emmet7life, 博文链接: https://www.jianshu.com/p/a5dfa5e6c721

[2] A/B Test样本量计算器, 工具链接: https://www.evanmiller.org/ab-testing/sample-size.html#!20;80;5;5;0

[3] AB test sample size calculation by hand - user3315198, 问答链接: https://stats.stackexchange.com/questions/392979/ab-test-sample-size-calculation-by-hand

[4] AB测试里的统计功效（Power）是个啥？- Nemo, 文章链接: https://zhuanlan.zhihu.com/p/149941019?from_voters_page=true

[5] Tang, D., Agarwal, A., O'Brien, D., & Meyer, M. (2010, July). Overlapping experiment infrastructure: More, better, faster experimentation. In Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 17-26).

[6] 假设检验、Z检验与T检验 - SUBHASH MEENA&VK, 文章链接: https://www.cnblogs.com/panchuangai/p/13215244.html

[7] P值 - 百度词条, 文章链接: https://baike.baidu.com/item/P值/7083622?fr=aladdin

[8] 假设检验-U检验、T检验、卡方检验、F检验 - J符离, 文章链接: https://blog.csdn.net/qq_22592457/article/details/92982170?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase

[9] Student's t-test, 维基百科: https://en.wikipedia.org/wiki/Student's_t-test#Independent_two-sample_t-test

[10] T Table, 博文链接: https://www.tdistributiontable.com/

[11] How to perform two-sample one-tailed t-test with numpy/scipy - stackoverflow, 问答链接: https://stackoverflow.com/questions/15984221/how-to-perform-two-sample-one-tailed-t-test-with-numpy-scipy

·················END·················

详解AB Test分析

推荐阅读