yyds！用机器学习预测 bilibili 股价走势-技术圈

本文主要讲解用Python分析哔哩哔哩股价，通过对股票数据进行基础分析，结合运用matplotlib绘图库进行可视化，并用机器学习方法 — 蒙特卡洛模拟预测未来一年股价走势。

安装

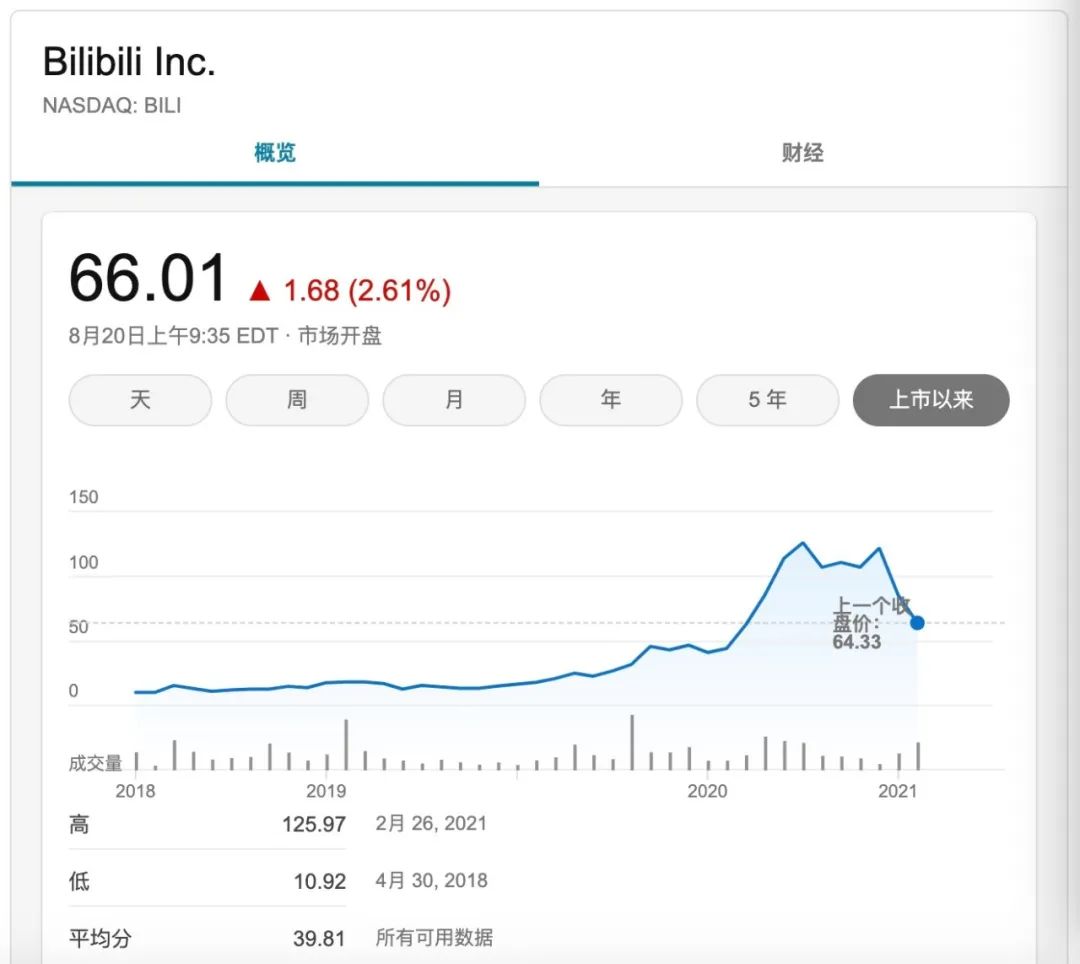
我们需要安装numpy、pandas、matplotlib、scipy等Python数据科学工具包。

#关注公众号：宽客邦，回复“源码”获取下载本文完整源码
import numpy as np
import pandas as pd
from math import sqrt
import matplotlib.pyplot as plt
from scipy.stats import norm
from pandas_datareader import data

选取哔哩哔哩（股票代码：BILI）2018年上市到现在2021年的数据进行分析，数据来自雅虎。这里使用pd.to_datetime将数据集时间转化为时间序列，便于股票的分析。

BILI = data.DataReader('BILI', 'yahoo',start='29/3/2018',)
BILI.index=pd.to_datetime(BILI.index)

首先用head()方法看一下数据集的结构，数据集包含了股票的开盘价、收盘价、每日最低价与最高价、交易量等信息。扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。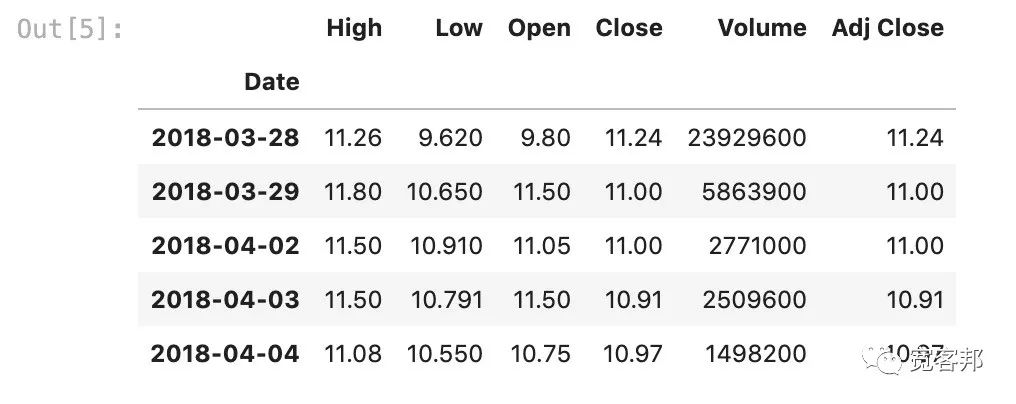

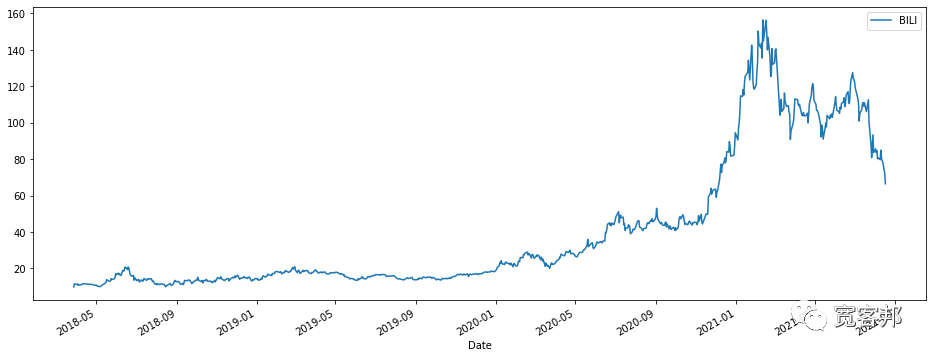
开盘价走势

我们可以通过 matplotlib 进行数据可视化，plt.legend用于设置图像的图例，loc是图例位置，upper right代表图例在右上角。从图中可以看出哔哩哔哩股票在2020年12月到2021年2月之间有一个快速的增长，随后股价有所回落。

plt.figure(figsize=(16,6))
BILI['Open'].plot()
plt.legend(['BILI'],loc='upper right')

股票成交量

我们再来看一下股票的成交量。

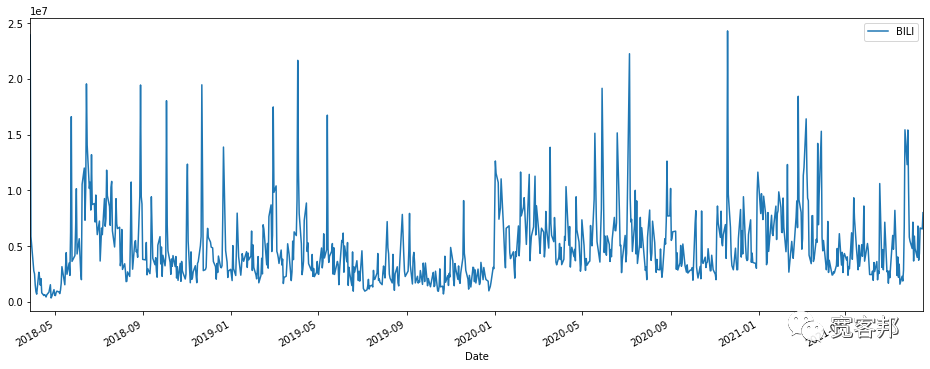
plt.figure(figsize=(16,6))
BILI['Volume'].plot()
plt.legend(['BILI'],loc='upper right')
plt.xlim(BILI.index[0],BILI.index[-1])

股票交易总额

我们再分析以下股票的交易总额。从图中可以很明显看出2021年1月到5月间某一天交易总额创历史新高。

BILI['Total Traded']=BILI['Open']*BILI['Volume']

plt.figure(figsize=(16,6))
BILI['Total Traded'].plot()

plt.legend(['BILI'],loc='upper right')
plt.xlim(BILI.index[0],BILI.index[-1])

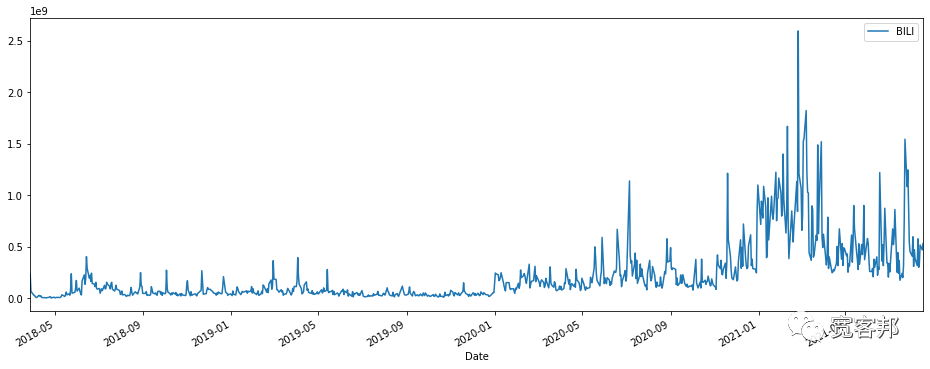
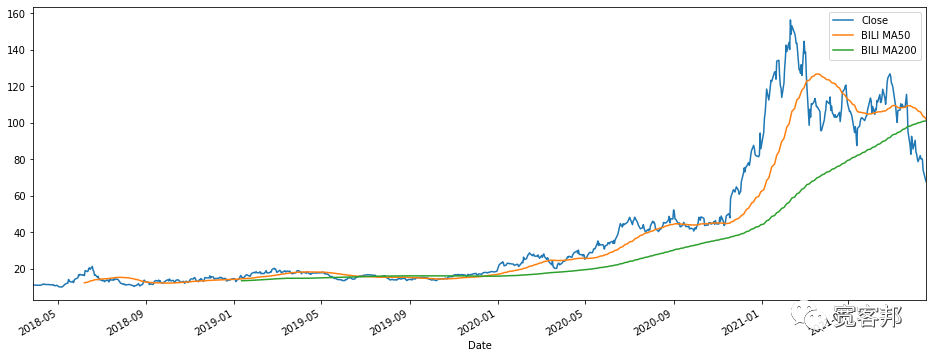
下面我们来通过argmax()获取最大交易总额的日期。

BILI['Total Traded'].argmax()

输出结果如下：

Timestamp('2021-02-25 00:00:00')

我们搜索新闻可以发现，2021年2月25日哔哩哔哩（NASDAQ: BILI）公布了截至2020年12月31日的第四季度和全年未经审计的财务报告。财报发布后，B站在美股的盘后股价一度涨超5%。

收盘价及其移动平均线

下面绘制BILI这支股票的收盘价及其移动平均线，我们可以用DataFrame的rolling()函数得到移动平均值。

BILI['Close'].plot(figsize=(16,6),xlim=(BILI.index[0],BILI.index[-1]))
BILI['Close'].rolling(50).mean().plot(label='BILI MA50')
BILI['Close'].rolling(200).mean().plot(label='BILI MA200')
plt.legend()

股票的收益率

下面我们计算每支股票的日收益率，并用直方图进行展示。这里了三种方法来计算日收益率，第一种是直接使用计算公式计算；第二种是导入专用于金融领域的第三方库ffn.to_returns函数计算；第三种是利用pandas自带的函数pct_change(1)进行计算。扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。

#关注公众号：宽客邦，回复“源码”获取完整源码，直接使用计算公式计算
BILI['Return']=(BILI['Close']-BILI['Close'].shift(1))/BILI['Close'].shift(1)
BILI=BILI.dropna()

#导入专用于金融领域的第三方库ffn.to_returns函数计算
import ffn
BILI['Return']=ffn.to_returns(BILI['Close'])

#利用pandas自带的函数pct_change(1)进行计算
BILI['Return']=BILI['Close'].pct_change()
BILI=BILI.dropna()

#关注公众号：宽客邦，回复“源码”获取下载本文完整源码
plt.hist(BILI['Return'],bins=50)

也可以用箱图观察收益率

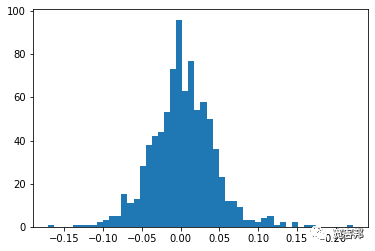
box_df = pd.concat([BILI['Return']],axis=1)
box_df.columns = ['BILI Returns']
box_df.plot(kind='box',figsize=(8,11),colormap='jet')

绘制股票的累计收益率

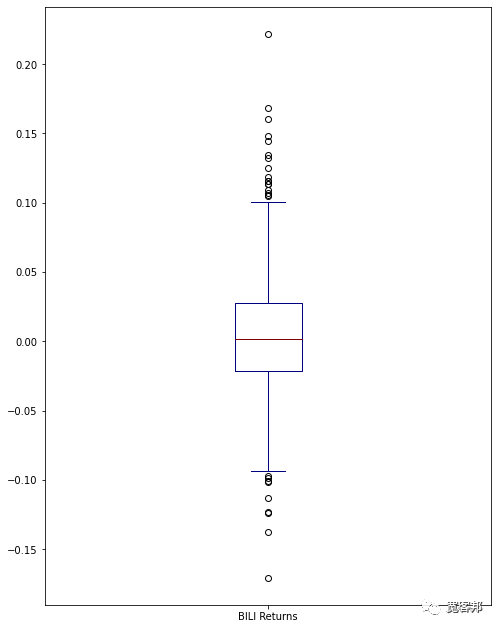
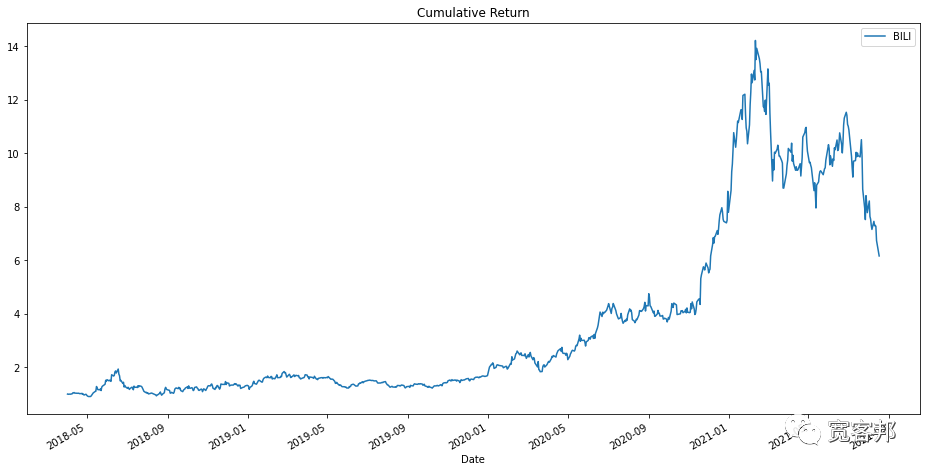
BILI['Cumulative Return']=(1+BILI['Return']).cumprod()

BILI['Cumulative Return'].plot(label='BILI',figsize=(16,8),title='Cumulative Return')
plt.legend()

股票的复合年均增长率和收益的年度波动率

计算股票的复合年均增长率和收益的年度波动率。

#关注公众号：宽客邦，回复“源码”获取完整源码，计算复合年均增长率
days = (BILI.index[-1] - BILI.index[0]).days
cagr = ((((BILI['Adj Close'][-1]) / BILI['Adj Close'][1])) ** (365.0/days)) - 1
print ('CAGR =',str(round(cagr)*100)+"%")
mu = cagr

#计算收益的年度波动率
BILI['Returns'] = BILI['Adj Close'].pct_change()
vol = BILI['Returns']*sqrt(252)
print ("Annual Volatility =",str(round(vol,4)*100)+"%")

CAGR = 71.72%Annual Volatility = 65.14%

用蒙特卡洛模拟预测股票走势

我们来预测未来一个交易年度（252 天）内潜在价格序列演变的单一模拟，基于遵循正态分布的每日收益随机的抽取。由第一个图表中显示的单线系列表示。第二个图表绘制了一年期间这些随机每日收益的直方图。扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。

S = BILI['Adj Close'][-1] #起始股票价格（即最后一天的实际股票价格）
T = 252 #交易天数
mu = 0.7172 #复合年均增长率
vol = 0.6514 #年度波动率

#关注公众号：宽客邦，回复“源码”获取完整源码，使用随机正态分布创建每日收益列表
daily_returns=np.random.normal((mu/T),vol/math.sqrt(T))+1

#关注公众号：宽客邦，回复“源码”获取下载本文完整源码
price_list = [S]

for x in daily_returns:
    price_list.append(price_list[-1]*x)

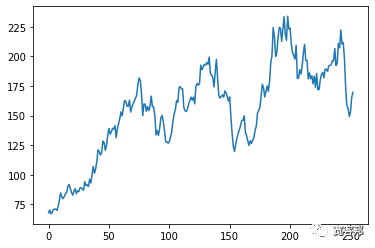
#生成价格序列的折线图

plt.plot(price_list)
plt.show()

生成每日收益的直方图

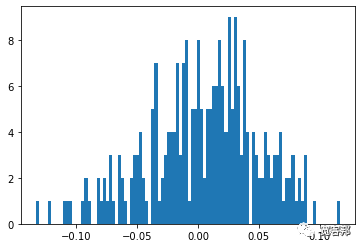
plt.hist(daily_returns-1, 100) 
plt.show()

1000次模拟预测未来哔哩哔哩股价走势。

import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.stats import norm

#关注公众号：宽客邦，回复“源码”获取下载本文完整源码
S = BILI['Adj Close'][-1] #起始股票价格（即最后一天的实际股票价格）
T = 252 #交易天数
mu = 0.7172 #复合年均增长率
vol = 0.6514 #年度波动率

#选择要模拟的运行次数 - 我选择1000
for i in range(1000):
    #使用随机正态分布创建每日收益列表
    daily_returns=np.random.normal(mu/T,vol/math.sqrt(T))+1
    
    #设置起始价格并创建由上述随机每日收益生成的价格列表
    price_list = [S]
    
    for x in daily_returns:
        price_list.append(price_list[-1]*x)

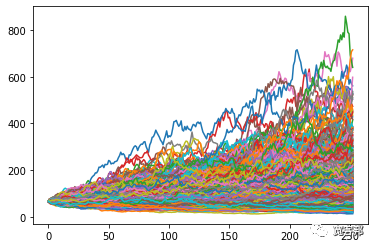
    #绘制来自每个单独运行的数据，我们将在最后绘制
    plt.plot(price_list)

#显示上面创建的多个价格系列的图
plt.show()

10000次模拟预测未来哔哩哔哩股价走势。

import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.stats import norm

#关注公众号：宽客邦，回复“源码”获取下载本文完整源码
result = []

#定义变量
S = BILI['Adj Close'][-1] #起始股票价格（即最后一天的实际股票价格）
T = 252 #交易天数
mu = 0.7172 #复合年均增长率
vol = 0.6514 #年度波动率

#选择要模拟的运行次数 - 选择10000
for i in range(10000):
    #使用随机正态分布创建每日收益列表
    daily_returns=np.random.normal(mu/T,vol/math.sqrt(T))+1
    
    #设置起始价格并创建由上述随机每日收益生成的价格列表
    price_list = [S]
    
    for x in daily_returns:
        price_list.append(price_list[-1]*x)

    #绘制来自每个单独运行的数据，我们将在最后绘制
    plt.plot(price_list)
    
    #将每次模拟运行的结束值附加到我们在开始时创建的空列表中
    result.append(price_list[-1])

#显示上面创建的多个价格系列的图
plt.show()

为我们的多重模拟创建股票收盘价的直方图。

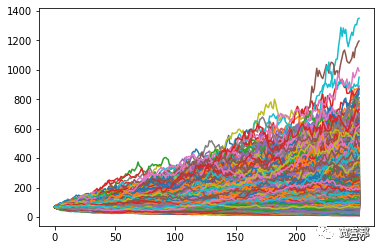
plt.hist(result,bins=50)
plt.show()

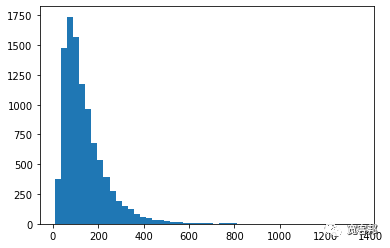
用numpy mean函数计算平均值的分布，以获得我们的“预期值”。

print(round(np.mean(result)))

139.18

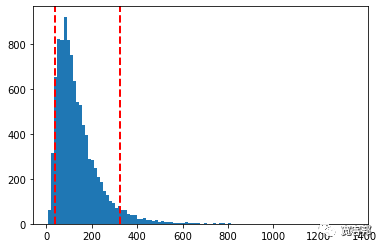
用 numpy 的“percentile”函数来计算 5% 和 95% 的分位数

print("5% quantile =",np.percentile(result,5))
print("95% quantile =",np.percentile(result,95))

5% quantile = 38.33550814175252

95% quantile = 326.44060907630484

在直方图上快速绘制我们刚刚计算的两个分位数，以给我们一个直观的表示。

plt.hist(result,bins=100)
plt.axvline(np.percentile(result,5), color='r', linestyle='dashed')
plt.axvline(np.percentile(result,95), color='r', linestyle='dashed')
plt.show()

从上面的结果我们得知：哔哩哔哩（BILI）的股价有5%的可能性最终会低于38.33美元，有5%的可能性会高于326.44美元。那么你是否愿意冒5%的风险获得股价低于38.33美元的损失，来追逐股价高于326.44美元的回报收益呢？扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。

↓↓长按扫码获取完整源码↓↓