激光点云的组织形式

• 什么是Kdtree

• 什么是Octree

• 对比总结

1. Kdtree的原理

Kdtree是一种划分k维数据空间的数据结构，在一个K维数据集合上构建一棵Kdtree代表了对该K维数据集合构成的K维空间的一个划分，即树中的每个结点就对应了一个K维的超矩形区域。主要用于多维空间关键数据的搜索。

2. Kdtree的创建

Kdtree的创建就是按照某种顺序将无序化的点云进行有序化排列，方便进行快捷高效的检索。算法流程如下：

（1） 在K维数据集合中选择具有最大方差的维度，然后在该维度上选择中值m为中心对该数据集合进行划分，得到两个子集合；同时创建一个树结点node，用于存储；

（2）对两个子集合重复（1）步骤的过程，直至所有子集合都不能再划分为止；如果某个子集合不能再划分时，则将该子集合中的数据保存到叶子结点。

根据上述算法步骤，以二维数据创建Kdtree为例，输入数据列表为{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}；划分的二维分割图如下：

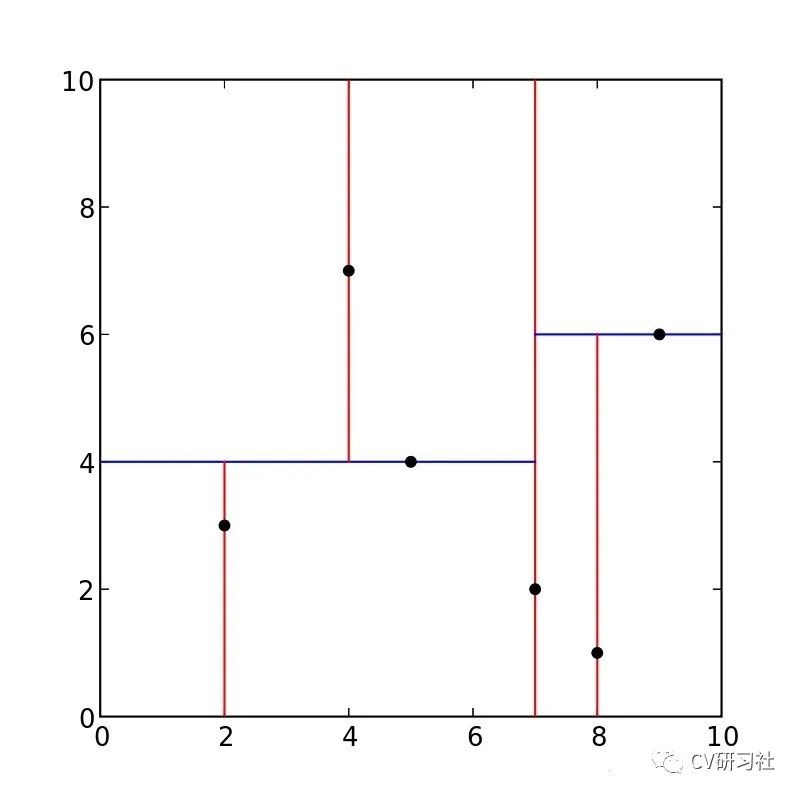
首先统计X和Y方向上的方差，选取方差较大的X维度作为初始分割轴，对X轴上的数值{2，5，9，4，8，7}取中值X=7作为分割线，生成左子树{(2,3)，(5,4)，(4,7)}，生成右子树{(9,6)，(8,1)}，更新分割轴Y，分别在左右子树中找到中位数（5,4）和（9,6），依次迭代如下图：

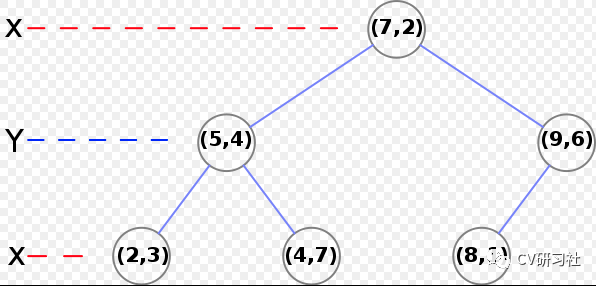
3. Kdtree的搜索

Kdtree的搜索方法有以下两种：

范围搜索：给定搜索点和搜索距离的阈值，从数据集中找出所有与搜索点距离小于阈值的数据；

最近邻搜索：给定查询点和正整数K，从数据集中找到距离查询点最近的K个数据，当K=1时，就是最近邻搜索。

以最近邻搜索算法为例，其流程如下：

（1）将查询数据Q从根结点开始，按照Q与各个结点的比较结果向下访问Kdtree，直至达到叶子结点。
其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与中值m进行比较，若Q(k) < m，则访问左子树，否则访问右子树。达到叶子结点时，计算Q与叶子结点上保存的数据之间的距离，记录下最小距离对应的数据点，记为当前最近邻点和最小距离Distance。

（2）进行回溯操作，该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点，它们之间的距离小于Distance。

如果Q与其父结点下的未被访问过的分支之间的距离小于Distance，则认为该分支中存在离P更近的数据，进入该结点，进行（1）步骤一样的查找过程，如果找到更近的数据点，则更新为当前的最近邻点，并更新Distance。

如果Q与其父结点下的未被访问过的分支之间的距离大于Distance，则说明该分支内不存在与Q更近的点。

回溯的判断过程是从下往上进行的，直到回溯到根结点时已经不存在与P更近的分支为止。

4. Kdtree的注意事项

a.对子空间进行划分时，怎样确定在哪个维度上划分？

轮流划分法：如果这次选择在第i维上进行数据划分，那下一次就在第j(j≠i)维上进行划分，例如：j = (i mod k) + 1。

但是这样忽略了不同属性数据之间的分散程度，有的属性值比较分散，有的属性值比较集中。当数据的分布在某一个维度较为集中，出现下图的现象，第一次划分将数据分为左右两个子集合，安装轮流的交替原则，第二次划分的轴并不能很好的分割数据：

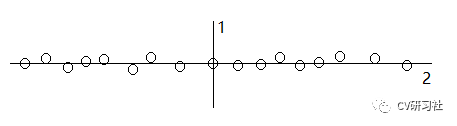
方差统计法：统计样本在每个维度上的数据方差，选出对应方差最大值的那个维度。因为方差大说明在该坐标轴上的数据点较为分散。

但是理论上空间均匀分布的点，在一个方向上分割之后，通过计算方差下一次分割就不会出现在这个方向上了，不过特殊情况如下：

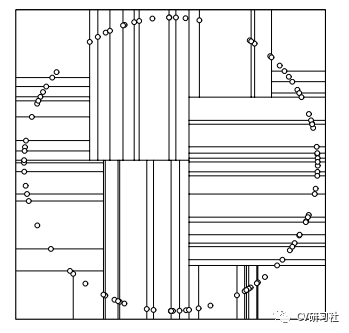
方差优化法：初始维度的划分依据数据方差范围最大的那一维作为分割维度，之后也是选中这个维度的中间节点作为轴点，然后进行分割，分割出来的结果如下图所示：

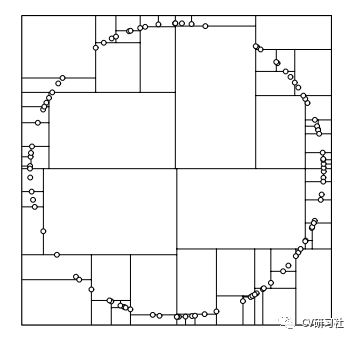
b.在某个维度上划分时，怎样确保树尽量平衡？

中位数法：找到该维度上数据的中位数，然后将数据点与中位数进行比较，得到两个子集合的个数基本相同。

c.怎样判断未被访问的分支里有离搜索数据更近的点？

从几何空间上，通过判断以搜索数据为中心和以记录的当前距离为半径的超球面与树分支代表的超矩形之间是否相交。如下图所示：

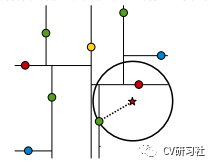
星号为搜索数据，绿色的点为疑似最近点，以搜索点和疑似最近点构成的圆与所在分割区域的矩形有交集，则需要回溯根节点中未被访问的分支。

1. Octree的原理

Octree是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素，每个节点有八个子节点，将八个子节点所表示的体积元素加在一起就等于父节点的体积。能够很好的压缩点云节省存储空间。

通过对三维空间的几何实体进行体元剖分，每个体元具有相同的时间和空间复杂度，通过循环递归的划分方法对大小为(2n∗2n∗2n) 的三维空间的几何对象进行剖分，从而构成一个具有根节点的方向图。在八叉树结构中如果被划分的体元具有相同的属性，则该体元构成一个叶节点；否则继续对该体元剖分成8个子立方体，依次递剖分，对于(2n∗2n∗2n)大小的空间对象，最多剖分n 次，如下图所示：

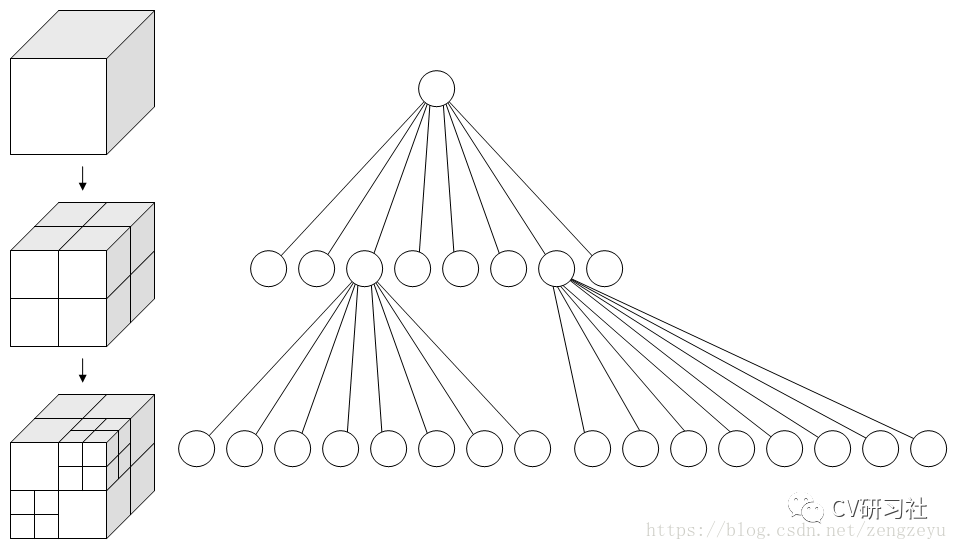
2. Octree的创建

（1）设定最大递归深度    

（2）找出场景的最大尺寸，并以此尺寸建立第一个立方体    

（3）依序将单位元元素丢入能被包含且没有子节点的立方体    

（4）若没有达到最大递归深度，就进行细分八等份，再将该立方体所装的单位元元素全部分担给八个子立方体    

（5）若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的，则该子立方体停止细分，因为根据空间分割理论，细分的空间所得到的分配必定较少，若是一样数目，则再怎么切数目还是一样，会造成无穷切割的情形。   

（5）重复3，直到达到最大递归深度。

Octree的叶子节点代表了分辨率最高的情况。例如分辨率设成0.01m，那么每个叶子就是一个1cm见方的小方块。如下图所示：

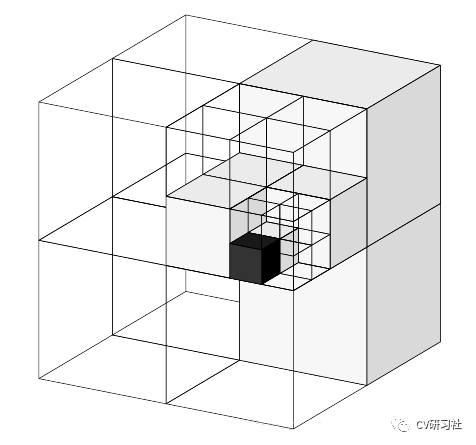
当分辨率较高时，方块很小；分辨率较低时，方块很大。以斯坦福课程中的兔子模型为例：

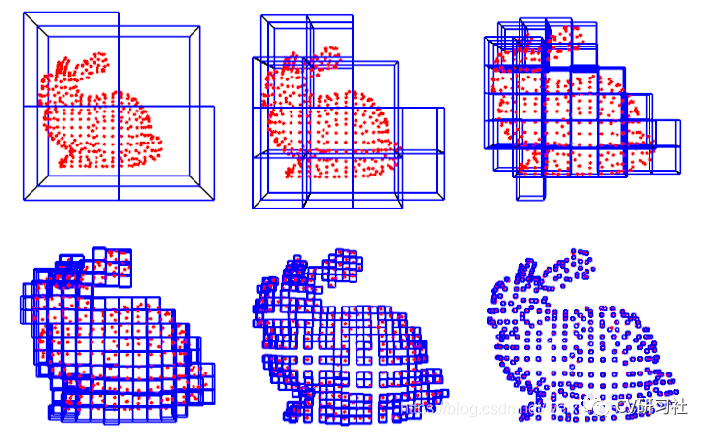
由于三维点云的数据量较大，使用Kdtree和Octree进行检索可以较少时间消耗，确保点云的关联点寻找和配准处于实时的状态。

Kdtree在邻域查找上比较有优势，但在大数据量的情况下，若划分粒度较小时，建树的开销也较大，但比八叉树灵活些。在小数据量的情况下，其搜索效率比较高，但在数据量增大的情况下，其效率会有一定的下降，一般是线性上升的规律。

Octree算法实现简单，但大数据量点云数据下，其使用比较困难的是最小粒度（叶节点）的确定，粒度较大时，有的节点数据量可能仍比较大，后续查询效率仍比较低，反之，粒度较小，八叉树的深度增加，需要的内存空间也比较大（每个非叶子节点需要八个指针），效率也降低。而等分的划分依据，使得在数据重心有偏斜的情况下，受划分深度限制，其效率不是太高。

如果将Octree和Kdtree结合起来的应用，应用八叉树进行大粒度的划分和查找，而后使用Kdtree树进行细分，效率会有一定的提升，但其搜索效率变化也与数据量的变化有一个线性关系。