本文我们将说明如何量化选择最佳模型过程中涉及的随机性。
kaggle比赛里经常会发生shake up的现象,说的直接点就是在有切榜或多榜单的比赛中,可能存在榜单排名激烈震动的情况,例如下面这个例子:Data Science Bowl 2017我们看到,第一名是从公榜上升了130多名,而第5名则上升了349。公榜结果就是好的模型私榜不一定就好,因为Kaggle是模拟real world的时刻在变化的数据,不一定遵从过去的规律,用过去的数据是无法确定就能预测未来的。一般情况下shake的原因可以归为如下几种:1.数据不同分布2.数据量太小3.异常值影响较大4.metric过于敏感5.模型太接近6.overfit等。那么第一名中的模型与第二名中的模型之间有什么区别呢?如果你的答案是:“区别在于,第一款模型比第二型模型更好,因为它具有较小的损失”,那么这个回答就太仓促了。事实上:我们如何才能确定测试集上更好的度量标准意味的是更好的模型,而不是一个更幸运的模型呢?
对于数据科学家来说,知道模型选择中哪一部分是偶然发挥的作用是一项基本技能。在本文中,我们将说明如何量化选择最佳模型过程中涉及的随机性。什么是“最好模型”?
假设有两个模型A和B,我们想选择最好的一个。最好的模型是在看不见的数据上表现最好的模型,这个应该是一个公认的判断方式。所以我们收集了一些测试数据(在训练期间没有使用的),并在此基础上评估我模型。假设模型A的ROC值为86%,模型B为85%。这是否意味着模型A比模型B更好?就目前我们掌握的信息而言:是的。但在一段时间之后,又收集了更多的数据并将其添加到测试集中。现在模型A仍然是86%,但模型B增加到87%。那么现在来说,B比A好了,对吧。对于一个给定的任务,最好的模型是在所有可能的不可见数据上表现最好的模型。
这个定义的重要部分是“所有可能”。我们能够访问的数据是有限的,所以测试数据集只是所有可能的不可见数据的一小部分。这就像是说我们永远都不知道什么才是最好的模型!Universe
我们将将所有可能的看不见数据的集合称为“Universe”。在现实世界中,我们永远无法观察到完整的Universe,而只有一个从Universe中随机采样的测试数据集。模型的真正性能是其在Universe上的性能, 在这种情况下该模型的真实ROC得分为80.4%。但是我们永远无法观察到Universe,我们永远无法观察到模型的真实ROC。我们观察到的是在测试集上计算的ROC分数。有时它会更高(81.6%),有时会更低(79.9%和78.5%),但是我们无法知道真正的ROC分数与观察到的ROC得分有多远。我们所能做的就是尝试评估该过程中涉及多少随机性。为此需要模拟Universe并从中取样许多随机测试数据集。这样我们就可以量化观察到的分数的离散度。如何模拟Universe?
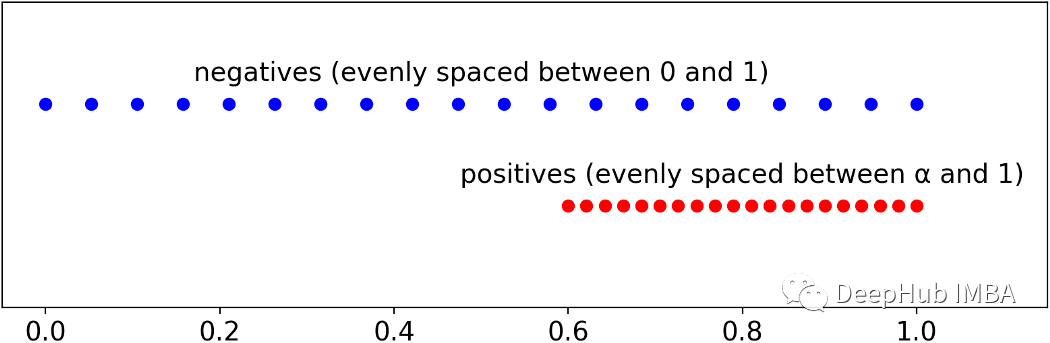
我们的目标是获得具有给定ROC评分的样本(观测结果),有一种非常简单的方法可以做到这一点。首先需要设定的所需的个体数量(通常是一个很大的数字)。然后设置流行率prevalence(上面的例子是2分类问题,所以只有正负样本),即阳性的百分比(可以将其保留为50%,这是默认值)。第三步是选择我们想要在Universe中的ROC分数。最后可以计算Universe中每个个体的预测概率:负的必须在0和1之间均匀间隔,而正的必须在α和1之间均匀间隔。 def get_y_proba(roc, n=100000, prevalence=.5): n_ones = int(round(n * prevalence)) n_zeros = n - n_ones y = np.array([0] * n_zeros + [1] * n_ones) alpha = (roc - .5) * 2
proba_zeros = np.linspace(0, 1, n_zeros) proba_ones = np.linspace(alpha, 1, n_ones) proba = np.concatenate([proba_zeros, proba_ones])
return y, proba
获取我们的不确定性
现在可以创建合成数据了,通过以下命令来获取universe: y_universe, proba_universe = get_y_proba(roc=.8, n=100000, prevalence=.5)
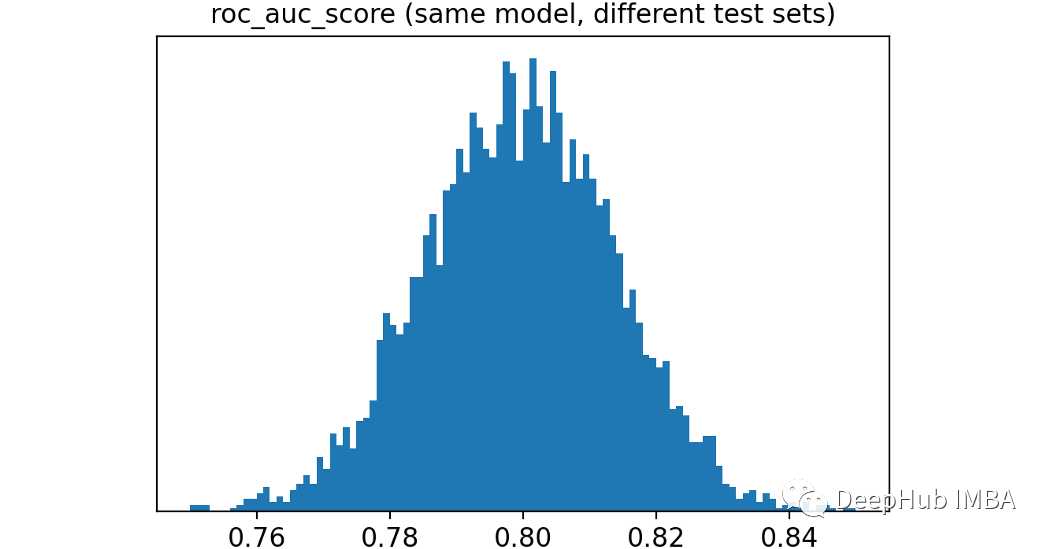
我们的全量数据(universe)是由10万次观测组成的,其中一半是真值的,ROC得分为80%。让我们模拟不同测试集的提取。每次将提取5000个不同的测试集,每个测试集包含1000个观测数据。这是相应的代码: rocs_sample = [] for i in range(5_000): index = np.random.choice(range(len(y_universe)), 1_000, replace=True) y_sample, proba_sample = y[index], proba[index] roc_sample = roc_auc_score(y_sample, proba_sample) rocs_sample.append(roc_sample)
可以看到结果是非常不同的,从低于76%到超过84%都会出现。在正常应用中,我们选择2个模型如下:一个ROC是78%,另一个是82%。他们有相同的潜在ROC,而这种差异只是偶然的结果的可能性有多大呢?为了给我们一个判断的依据,可以计算模拟中每对观察到的ROC得分之间的距离。Scikit-learn有一个pairwise_distance函数可以实现这一点。 import numpy as np from sklearn.metrics import pairwise_distances
dist = pairwise_distances(np.array(rocs_sample).reshape(-1,1)) dist = dist[np.triu_indices(len(rocs_sample), k=1)]
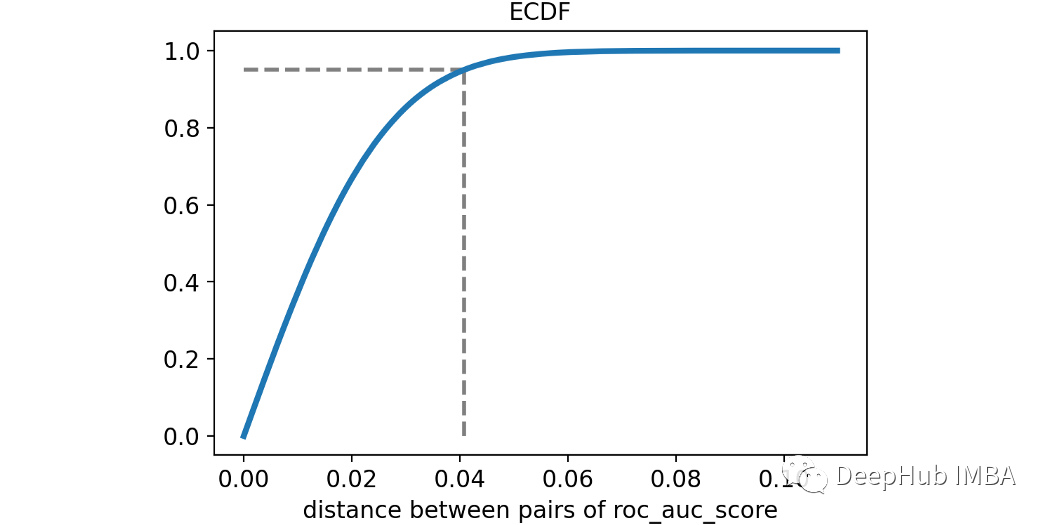
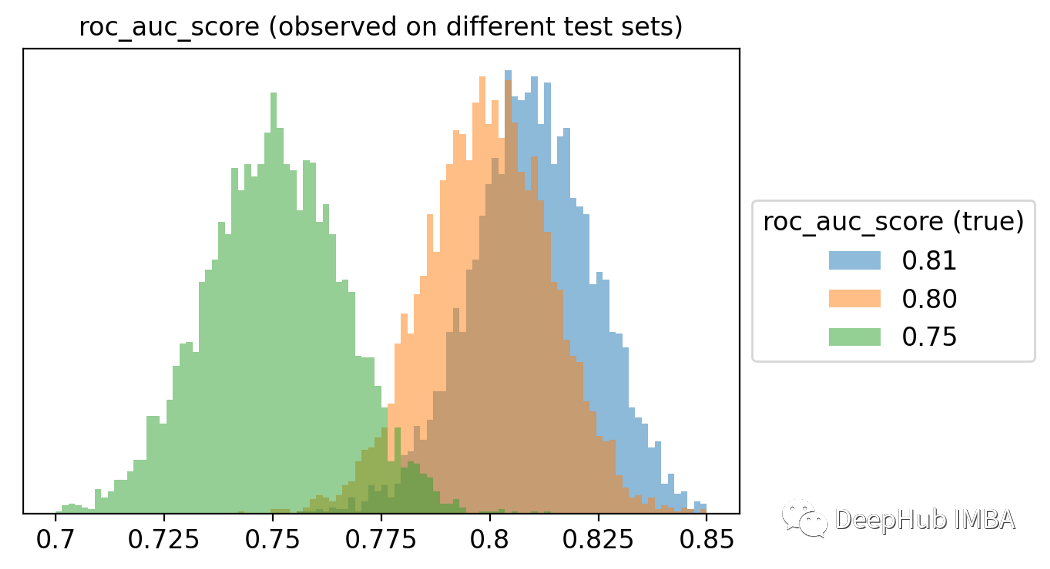
让我们用经验累积分布函数来可视化ROC得分之间的两两距离。第95个百分位(用虚线突出显示)约为4%。这意味着两种模型(性能相同)之间的差异只有5%的时间大于4%。使用统计术语我们会说:小于4%的差异不显著!这很有趣,因为通常我们会认为82%的ROC模型比78%的ROC模型要好得多。为了获得这个概念的另一个可视化,我模拟了三个不同的universe,一个的ROC值为75%,另一个为80%,最后一个为81%。这些是观察到的ROC评分的分布。从上图中可以明显看出,最好的模型通常不会获胜!想象一下,比较几十个模型,每个模型的真实ROC得分都不同。也就是说选择可能不是最好的模型。而是选择了一个最幸运的。还能做点什么吗?
上面的描述都说明了一个问题:没有办法100%确定一个模型比另一个更好,这听起来像一场噩梦。当然:在数据科学中不存在100%的确定性,但是我们还是有一些小小的技巧。选择最佳模型的不确定性程度既取决于universe的特征,也取决于从universe中提取的测试集的特征。这里有三个参数控制着不确定性:- 真实ROC:在universe中计算的ROC得分(这个肯定是得不到的,所以只能假设)。
- 样本流行率(prevalence):测试集中的阳性百分比。
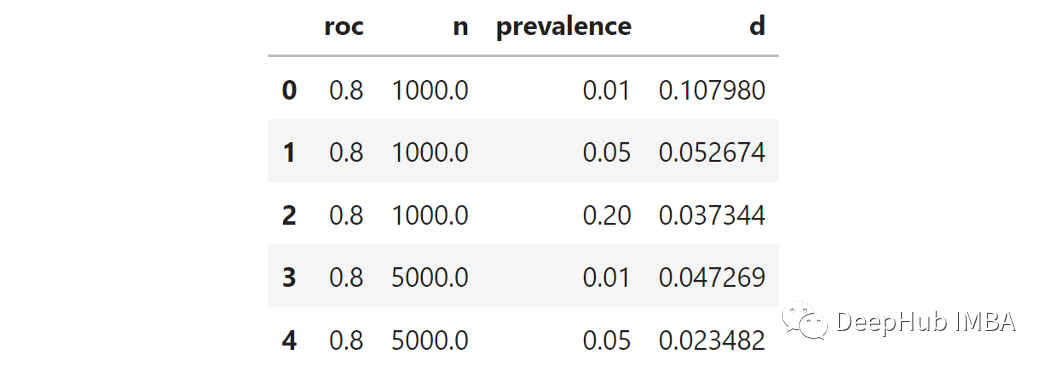
为了了解这些元素对不确定性的影响,可以尝试每个元素的不同值来模拟发生的情况:因为我们要为三个参数尝试三个值,这意味着27种可能的组合。对于每个组合,我都可以使用上面的函数创建模拟universe,然后采样了1000个不同的测试集,并测量了各自的ROC得分。然后计算1000个ROC得分的距离矩阵。最后取距离的第95个百分位数(从现在开始称为“d”)。这就是上面所说的,对选择模型的不确定性的衡量。
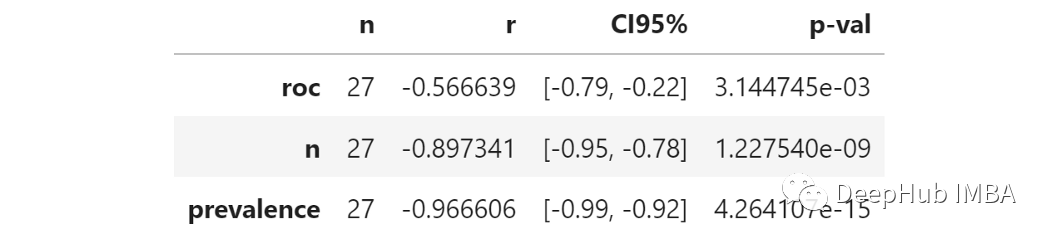
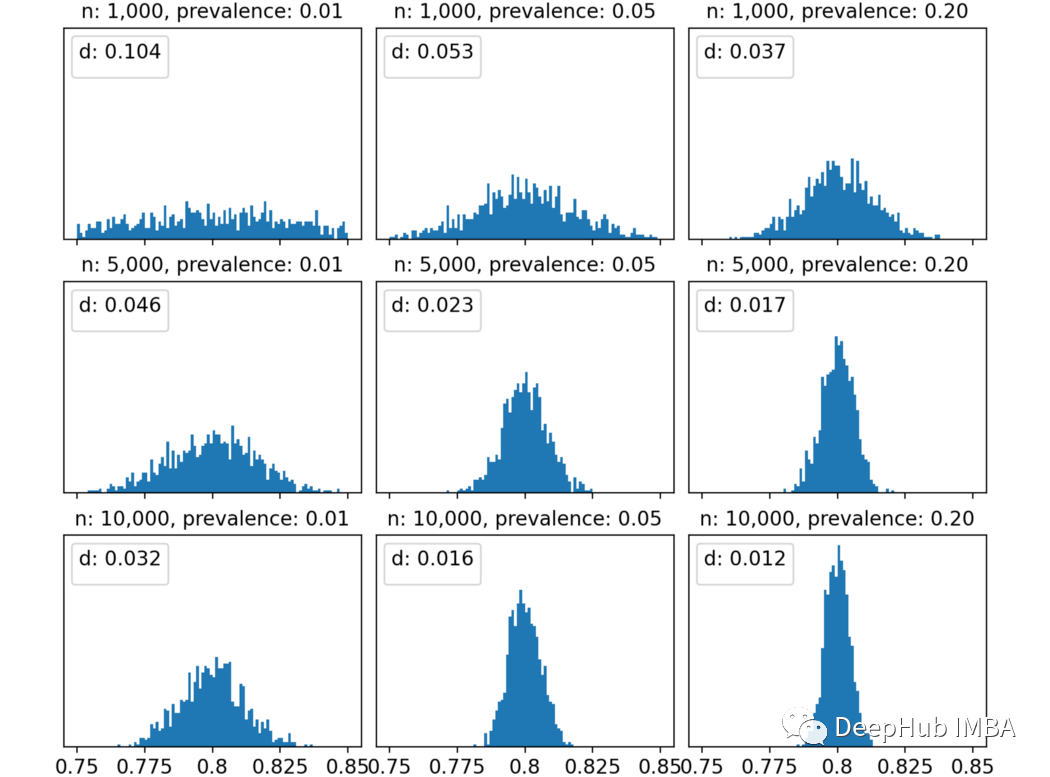
我们用95百分位测量不确定性。这个数字越高,ROC曲线比较的不确定性就越高。由于我们想知道不确定性如何取决于3个参数,那么测量每个参数和“ D”之间的相关性能代表什么呢?这就是结果:称为“ R”的列显示了每个参数和不确定性之间的部分相关性。所有相关系数均为阴性,表明增加了这三个中的任何一个都会降低不确定性。真实ROC:全量数据中的ROC得分较高意味着不确定性较小。这是有道理的,因为根据定义,更高的ROC意味着较小程度的不确定性。样本数:增加样品数会可降低不确定性。这很明显,并且在统计数据中一直存在。样本流行率:增加流行率会降低不确定性。较小的流行率意味着更少的阳性。更少的阳性意味着在抽样时随机性的权重更大, 因此有更大的不确定性。出于好奇心,对于固定的真实ROC(在这种情况下为80%)时,当改变样本数和样本流行率时,我们看看得到的ROC分数的分布。我认为这张图很明显。以左上角为例:样本数和流行率都非常小,我们有1000个观察结果和1%的阳性结果,这意味着10个阳性结果和990个阴性结果,在这种情况下不确定性非常高,得到的ROC评分分布几乎是均匀的,从75%到85%。ROC评分之间的距离的第95百分位数为10%,这意味着观察到的ROC值为75%与观察到的ROC值为85%之间没有显著差异。然而随着逐步提高样本维度数/或流行率,观察到的ROC评分分布越来越集中在真实值附近(本例中为80%)。例如,10000样本和20%的流行率,第95个百分位数变成了更合理的1.2%。这对我有用吗?
应该会有一点用,因为我们要知道在哪些条件下模型的结果在统计上是合理的。例如重复像在上面看到模拟会帮助你知道测试集的数值和流行率是否足以检测模型性能之间的真正差异。如果还是无法模拟的话,那就Trust your CV 吧,其实我们的CV也降低了我们模型的随机性。