下面这篇揭示了矩阵的基本子空间理论可以很好地解释降维算法的原理。

从奇异值分解 SVD 看 PCA

实际上，子空间还可以拿来解释线性最小二乘法。我们用一个简单例子来直观地分析最小二乘问题及其解法。

1问题

假设我们要通过在弹簧上附加不同的重量并测量其长度来确定弹簧的弹性系数。

我们知道长度 取决于力 ，具体来说，可以根据胡克定律的公式

其中， 和 是待确定的常数。

假设我们已经进行了实验并获得了以下数据，

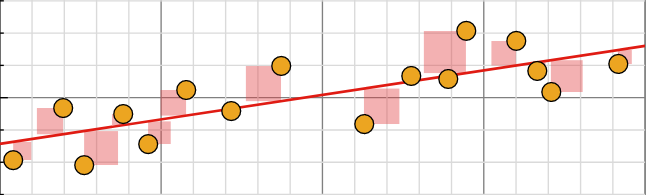
我们绘制了相应的散点图，显然这些点并不在一条直线上。这意味着我们不能精确地求得上面那两个待定常数。

由于测量中的误差不可避免，我们希望使用获得的所有数据以最大程度地减少误差的影响。因此引入了一个数据量超过未知数个数的线性方程组，即所谓的超定方程组，

或以矩阵形式写为，

我们将使用最小二乘法确定弹簧的弹性常数的近似值。

令 ，线性方程组

称为超定方程组：其方程式的个数多于未知数的个数。

2几何上直观来看

通常，上面这种方程组并没有解。例如，当 和 时，可以从几何上直观得看出这一点。

我们在 空间中考虑两个向量 和 ，上面的问题相当于要找到这两个向量的一个线性组合，使得

如下图所示，可以看到这样的问题通常并不能找到解。两个向量 和 张成一个平面，如果右侧的 不在该平面中，则并不存在 和 的一个线性组合使得 成立。

在这种情况下，求解线性方程组的一个明显替代方案是使如下向量，

尽可能地小。

这里， 称为残差向量。这个替代问题的解取决于我们如何测量残差向量的长度。

在最小二乘法中，我们使用标准的欧几里得范数。因此，我们想找到使如下式子最小化的向量 ，

由于未知向量 在上式中是以线性形式出现的，因此也称为线性最小二乘问题。

在该例子中，凭我们对 空间中距离的了解可以知道，如果我们选择平面中使得残差向量正交于平面，则向量 的末端与平面之间的距离将最小化。

由于矩阵 的列张成整个平面，因此我们可以通过使 正交于 的列来求得解。对于一般情况，这种几何直觉也是有效的，即有

可以写成如下矩阵形式，

然后，代入 得到法方程，

求解上述方程组，可得解 。

3法方程

定理

假设 的列向量是线性独立的，则法方程

有唯一解。

证明

我们首先证明 是正定的。令 为任意非零向量。然后，根据线性独立性的定义，可得 。由于 ，于是

等价于 是正定的。因此， 是非奇异的，并且法方程具有唯一解，将其表示为 。

然后，我们证明 是最小二乘问题的解，即对于所有的 都有 ，其中 。

可以将 写为，

于是有，

由于 ，上式中间两项等于零，我们得

证毕。

缺点

然而，用法方程解线性最小二乘问题有两个明显的缺点，

1. 计算 可能导致信息丢失。

2. 的条件数是 的条件数的平方，即

我们通过一个示例来说明第 1 点。

例子

给定 ，定义如下矩阵，

于是有，

假设 很小，以至于 的浮点表示满足 ，因此在浮点运算中，该法方程是奇异的。这相当于在 中丢失了 中存在的重要信息。

4使用 SVD 求解

最小二乘问题可以使用 SVD 来求解。假设我们有一个待定的线性方程组 ，其中矩阵 为列满秩。

矩阵 的 SVD 分解如下，

其中 。利用 SVD 和正交变换下范数不变的事实，得

其中， 以及 。从而

现在，我们可以通过解 来最小化 ，即最小二乘解由下式给出，

由于 是对角矩阵，即

所以解也可以写成，

列满秩的假设意味着所有奇异值都不为零:。我们还看到，在这种情况下，解是唯一的。

下面将上述内容概括总结一下。

.基于 SVD 的最小二乘解

已知矩阵 是列满秩的，并且它的精简版 SVD 分解为 。

然后最小二乘问题，

有如下唯一解，

.SVD 求解过程的几何解释

我们再次来看这个超定线性方程组，

结合下面这篇里的子空间理论，

从奇异值分解看四个基本子空间

求解上面方程组相当于要从矩阵 的列空间里找向量 的系数 。

但是，这里的问题就出在向量  往往并不在矩阵 的列空间里，所以只能退而求其次，在列空间里找到一个向量，使之与 的残差向量 的长度最小。

我们再来看一下解，

结合下图，我们把上式一步步来解读一下。

从右往左看， 表示向量 往列空间的正交坐标系 里投影得到新的坐标。这个就是上图中平面内的黄色虚箭头表示的向量在坐标系 里的坐标，

但这个坐标并不是我们要的解，因为最终要的解是相对矩阵 的列来说的坐标。

现在来看黄色虚线向量，即

我们要找的是使下式成立的 ，

把 SVD 分解 代入上式，得

两边左乘 ，

由于矩阵 是列满秩的，因此得唯一解，

.用线性变换来解释

我们知道，矩阵 表示的线性变换在基 和基 之间可以用矩阵 表示。

现在，黄色虚向量 在基 下的坐标为 ，可以通过逆变换 得到待求解在基 下的坐标 ，对应的向量正是 ，即 。

正向验证一下，坐标 经矩阵 变换后为 ，这正是黄色虚向量 在基 下的坐标。

.伪逆（广义逆矩阵）

我们再次看上面得到的解，

这里可以引出一个概念，那就是伪逆。

但是，要注意的是这里的矩阵不要求列满秩。

定义 矩阵 的一个奇异值分解为 ，则 的伪逆为，

其中，

有了系数矩阵的伪逆，上面最小二乘问题的解是不是可以写得更简洁呢？

5收尾

本篇讲的是线性最小二乘问题，除了上面的解法还有很多其他方法，如求导、 分解等。

另外，最小二乘有线性问题，自然也有非线性问题。那么所谓的非线性最小二乘问题会是怎么样呢？以及如何求解呢？这些问题后续展开。

.相关阅读