【统计学习方法】 从零开始,用python实现最小二乘法

点击上方“公众号”可订阅哦!
本文主要介绍使用Numpy中的poly1d()多项式函数和Scipy的optimize模块的leastsq()函数,分别使用它们作为拟合函数和最小二乘法实现对数据的拟合。
1
●
poly1d()函数
np.poly1d(c_or_r, r=False, variable=None)
该函数包括三个参数,下面分别介绍这三个参数。
c_or_r:类似数组,多项式的系数,以幂次递减,或者当第二个参数的值为True,即多项式的根(多项式求值为0的值)。
``poly1d([1,2,3])``
返回一个表示以下内容的对象:
math:`x ^ 2 + 2x + 3`,
而``poly1d([1,2,3],True)``
返回一个代表:
math:`(x-1)(x-2)(x-3)= x ^ 3-6x ^ 2 + 11x -6`。
r=False:布尔型,可选如果为True,则`c_or_r`指定多项式的根。默认为False。
variable:str,可选将打印p时使用的变量从x更改为variable。
p = np.poly1d([1, 2, 3])print(np.poly1d(p))# output21 x + 2 x + 3p(0.5)# output 计算当x为0.5时函数值4.25p.r# output 计算函数根array([-1.+1.41421356j, -1.-1.41421356j])p.c# output 现实系数array([1, 2, 3])p[1]# output 显示多项式中第k次幂的系数2p * p# output 多项式相乘poly1d([ 1, 4, 10, 12, 9])p = np.poly1d([1,2,3], variable='z')print(p)# output21 z + 2 z + 3# 从其根构造一个多项式:np.poly1d([1, 2], True)# outputpoly1d([ 1, -3, 2])
2
●
leastsq()函数
首先来看leastsq()函数的参数,
leastsq(func,x0,args=(),Dfun=None,full_output=0,col_deriv=0,ftol=1.49012e-08,xtol=1.49012e-08,gtol=0.0,maxfev=0,epsfcn=None,factor=100,diag=None,)
参数还是非常多的,一般来说,我们只需要前三个参数就够了,
他们的作用分别是:
func:误差函数
x0:表示函数的参数
args=():表示数据点
3
●
使用最小二乘法进行数据拟合
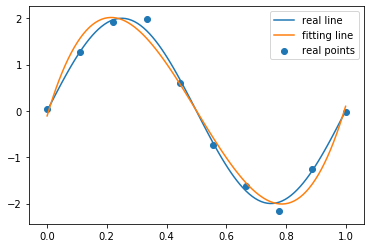
import numpy as npimport scipy as spfrom scipy.optimize import leastsqimport matplotlib.pyplot as plt%matplotlib inlinedef func(x):return 2*np.sin(2*np.pi*x)def residuals(p, x, y):fun = np.poly1d(p) # poly1d()函数可以按照输入的列表p返回一个多项式函数return y - fun(x) # 返回真实值 与我们拟合的曲线上对应的值的差# 拟合函数def fitting(p):pars = np.random.rand(p+1) # 生成p+1个随机数的列表,这样poly1d函数返回的多项式次数就是pr = leastsq(residuals, pars, args=(X, Y)) # 三个参数:误差函数、函数参数列表、数据点return r# 要进行拟合的数据点X = np.linspace(0, 1, 10)Y = [np.random.normal(0, 0.1)+num for num in func(X)] # 添加噪声# 方便绘制曲线,所以创建多一些点x_ = np.linspace(0, 1, 100)y_ = func(x_)fit_pars = fitting(3)[0] # 注意返回值中的第一行才是拟合曲线的参数列表plt.plot(x_, y_, label='real line')plt.scatter(X, Y, label='real points')plt.plot(x_, np.poly1d(fit_pars)(x_), label='fitting line')plt.legend()plt.show()
END
扫码关注
微信号|sdxx_rmbj
评论
