Python数学建模系列（六）：蒙特卡洛算法
1、蒙特卡洛算法
什么是蒙特卡洛算法？
❝蒙特·卡罗（ Monte Carlo method），又称统计模拟方法，是二十世纪四十年代中叶由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。
❞
起源：
❝蒙特卡洛方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划成员S.M.乌拉姆和J.冯·诺依曼首先提出。数学家冯·诺依曼用驰名世界的赌城——摩纳哥的Monte Carlo——来命名这种方法，为它蒙上一层神秘色彩。公认的蒙特卡洛方法的起源是1777年法国数学家布丰提出用投针实验的方法求圆周率π。
❞
基本思想：
❝当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。
❞
工作步骤：
构造或描述概率过程 实现从已知概率分布抽样 建立各种估计量
样例1
题目：经典的蒙特卡洛方法求圆周率
❝基本思想：在图中区域产生足够多的随机数点，然后计算落在圆内的点的个数与总个数的比值再乘以4，就是圆周率。
❞
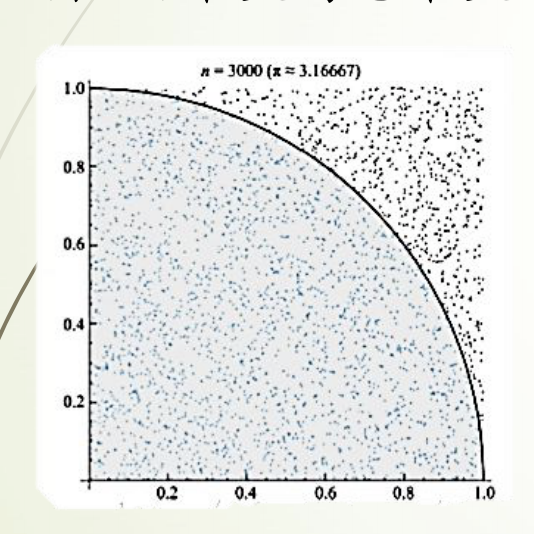Demo代码 「（模拟次数为10000次时）」
import math
import random
m = 10000
n = 0
for i in range(m):
# x、y为0-1之间的随机数
x = random.random()
y = random.random()
# 若点(x,y) 属于图中1/4圆内 则有效个数+1
if math.sqrt(x**2 + y**2) < 1:
n += 1
# 计算pi
pi = 4 * n / m
print("pi = {}".format(pi))
# pi = 3.1508（结果具有随机性 不一定完全一样）
Demo代码 「（模拟次数为1000000次时）」
import math
import random
m = 1000000
n = 0
for i in range(m):
x = random.random()
y = random.random()
if math.sqrt(x**2 + y**2) < 1:
n += 1
pi = 4 * n / m
print("pi = {}".format(pi))
# pi = 3.141416
样例2
利用python计算函数在[0,1]区间的定积分
Demo代码
import math
import random
m = 1000000
n = 0
for i in range(m):
x = random.random()
y = random.random()
if y >= x**2:
n += 1
r = n / m
print("r = {}".format(r))
# r = 0.666817
变式：计算积分
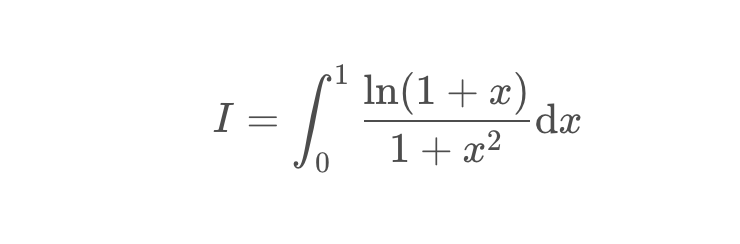
❝题目来源：https://blog.csdn.net/FightingBob/article/details/109694130
理论答案：
❞
先绘制函数图像：
import numpy as np
import matplotlib.pylab as plt
x = np.linspace(0,1,num=50)
y = np.log(1 + x) / (1 + x**2)
plt.plot(x,y,'-')
函数图像如下：
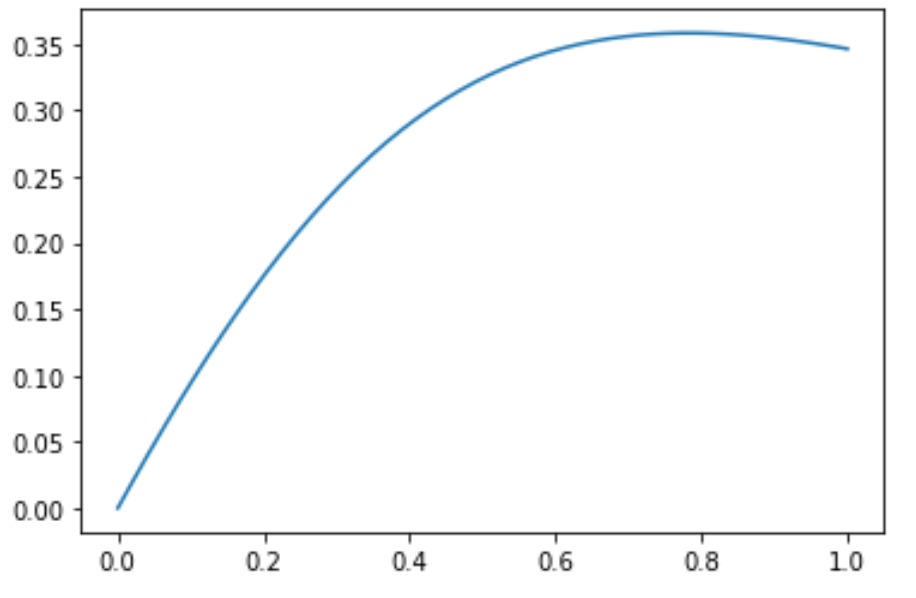计算积分
import numpy as np
import random
m = 100000
n = 0
for i in range(m):
x = random.random()
y = random.random()
if np.log(1 + x) / (1 + x**2) > y:
n += 1
ans = n / m
ans
# 0.27293
# 理论答案是 pi/8*log(2) = 0.2721983
样例3
现在有个项目，共三个WBS要素，分别是设计、建造和测试。假设这三个WBS要素预估工期的概率分布呈标准正态分布，且三者之间都是完成到开始的逻辑关系，于是整个项目工期就是三个WBS要素工期之和。
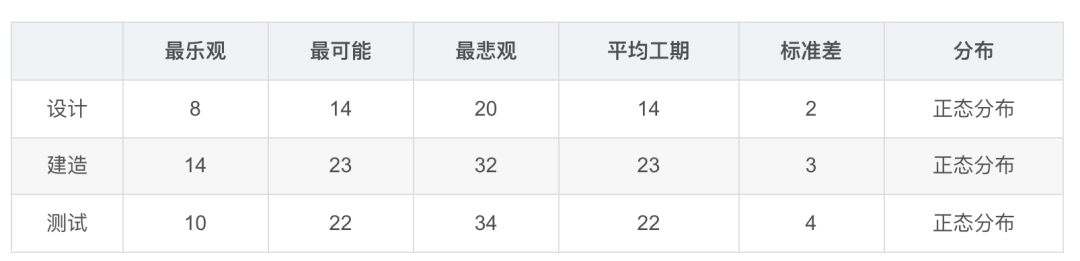
首先，先画出这三个要素的概率密度函数
从表中可以看出 时间最少为8天 最长为34天 所以我们设置时间范围为7-35 天
import numpy as np
import matplotlib.pyplot as plt
import math
def normal_distribution(x, mean, sigma):
return np.exp(-1*((x-mean)**2)/(2*(sigma**2)))/(math.sqrt(2*np.pi) * sigma)
mean1, sigma1 = 14, 2
x1 = np.linspace(7, 35,num=100)
mean2, sigma2 = 23, 3
x2 = np.linspace(7, 35, num=100)
mean3, sigma3 =22, 4
x3 = np.linspace(7, 35, num=100)
y1 = normal_distribution(x1, mean1, sigma1)
y2 = normal_distribution(x2, mean2, sigma2)
y3 = normal_distribution(x3, mean3, sigma3)
plt.plot(x1, y1, 'r', label='m=14,sig=2')
plt.plot(x2, y2, 'g', label='m=23,sig=3')
plt.plot(x3, y3, 'b', label='m=22,sig=4')
plt.legend()
plt.grid()
plt.show()
图像如下：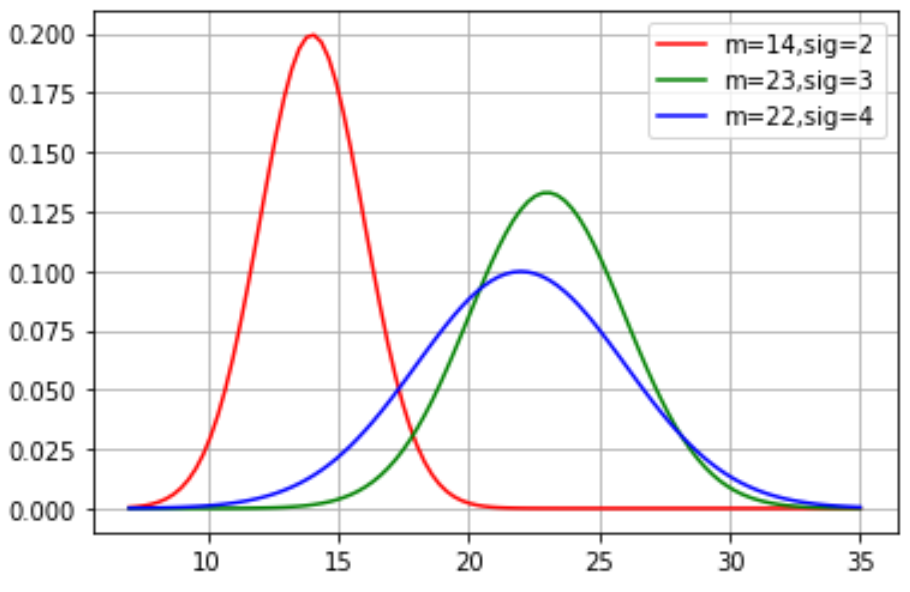
Demo代码
import numpy as np
import matplotlib.pylab as plt
import random
import math
m = 10000
a = 0
b = 0
y1 = np.random.normal(loc=14,scale=2,size=m)
y2 = np.random.normal(loc=23,scale=3,size=m)
y3 = np.random.normal(loc=22,scale=4,size=m)
y =y1 + y2 + y3
a,b = np.mean(y),np.var(y)
a,b
# (59.08396232409535, 29.120136564111085)
# 理论均值为59 = 14 + 23 + 22 方差为29 = 2*2 + 3*3 + 4*4
2、三门问题
三门问题
❝三门问题（Monty Hall probelm）亦称为蒙提霍尔问题，出自美国电视游戏节目Let’s Make a Deal。
参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门则各藏有一只山羊。
当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后问参赛者要不要换另一扇仍然关上的门。
问题是：换另一扇门是否会增加参赛者赢得汽车的几率？如果严格按照上述条件，即主持人清楚地知道，自己打开的那扇门后面是羊，那么答案是会。不换门的话，赢得汽车的几率是1/3,，换门的话，赢得汽车的几率是2/3。
❞
蒙特卡洛思想的应用
❝应用蒙特卡洛重点在使用随机数来模拟类似于赌博问题的赢率问题，并且通过多次模拟得到所要计算值的模拟值。
在三门问题中，用0、1、2分代表三扇门的编号，在[0,2]之间随机生成一个整数代表奖品所在门的编号prize，再次在[0,2]之间随机生成一个整数代表参赛者所选择的门的编号guess。用变量change代表游戏中的换门（true）与不换门（false）。
❞
蒙特卡洛过程
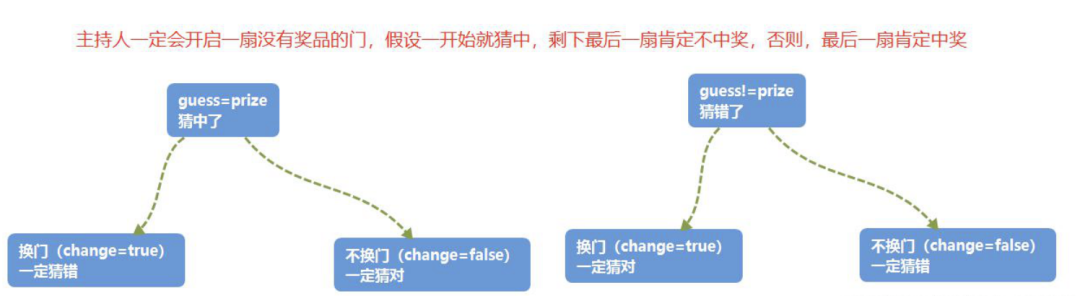Demo代码
import math
def play(change):
prize = random.randint(0,2)
guess = random.randint(0,2)
if guess == prize:
if change:
return False
else:
return True
else:
if change:
return True
else:
return False
def winRate(change, N):
win = 0
for i in range(N):
if(play(change)):
win += 1
print("中奖率为{}".format(win / N))
N = 1000000
print("每次换门的中奖概率：")
winRate(True,N)
print("每次都不换门的中奖概率：")
winRate(False,N)
# 理论换门2/3 不换门1/3
#每次换门的中奖概率：
#中奖率为0.665769
#每次都不换门的中奖概率：
#中奖率为0.33292
运行结果
3、M*M豆问题
M*M豆贝叶斯统计问题
❝M&M豆是有各种颜色的糖果巧克力豆。制造M&M豆的Mars公司会不时变更不同颜色巧克力豆之间的混合比例。
1995年，他们推出了蓝色的M&M豆。在此前一袋普通的M&M豆中，颜色的搭配为：30%褐色，20%黄色，20%红色，10%绿色，10%橙色，10%黄褐色。这之后变成了：24%蓝色，20%绿色，16%橙色，14%黄色，13%红色，13%褐色。
假设我的一个朋友有两袋M&M豆，他告诉我一袋是1994年，一带是1996年。
但他没告诉我具体那个袋子是哪一年的，他从每个袋子里各取了一个M&M豆给我。一个是黄色，一个是绿色的。那么黄色豆来自1994年的袋子的概率是多少？
❞
Demo代码
import time
import random
for i in range(10):
print(time.strftime("%Y-%m-%d %X",time.localtime()))
dou = {1994:{'褐色':30,'黄色':20,'红色':20,'绿色':10,'橙色':10,'黄褐':30},
1996:{'蓝色':24,'绿色':20,'橙色':16,'黄色':14,'红色':13,'褐色':13}}
num = 10000
list_1994 = ['褐色']*30*num+['黄色']*20*num+['红色']*20*num+['绿色']*10*num+['橙色']*10*num+['黄褐']*10*num
list_1996 = ['蓝色']*24*num+['绿色']*20*num+['橙色']*16*num+['黄色']*14*num+['红色']*13*num+['褐色']*13*num
random.shuffle(list_1994)
random.shuffle(list_1996)
count_all = 0
count_key = 0
for key in range(100 * num):
if list_1994[key] == '黄色' and list_1996[key] == '绿色':
count_all += 1
count_key += 1
if list_1994[key] == '绿色' and list_1996[key] == '黄色':
count_all += 1
print(count_key / count_all,20/27)
print(time.strftime("%Y-%m-%d %X",time.localtime()))
# ...
# 0.7407064573459715 0.7407407407407407
# 20/27是理论答案
运行结果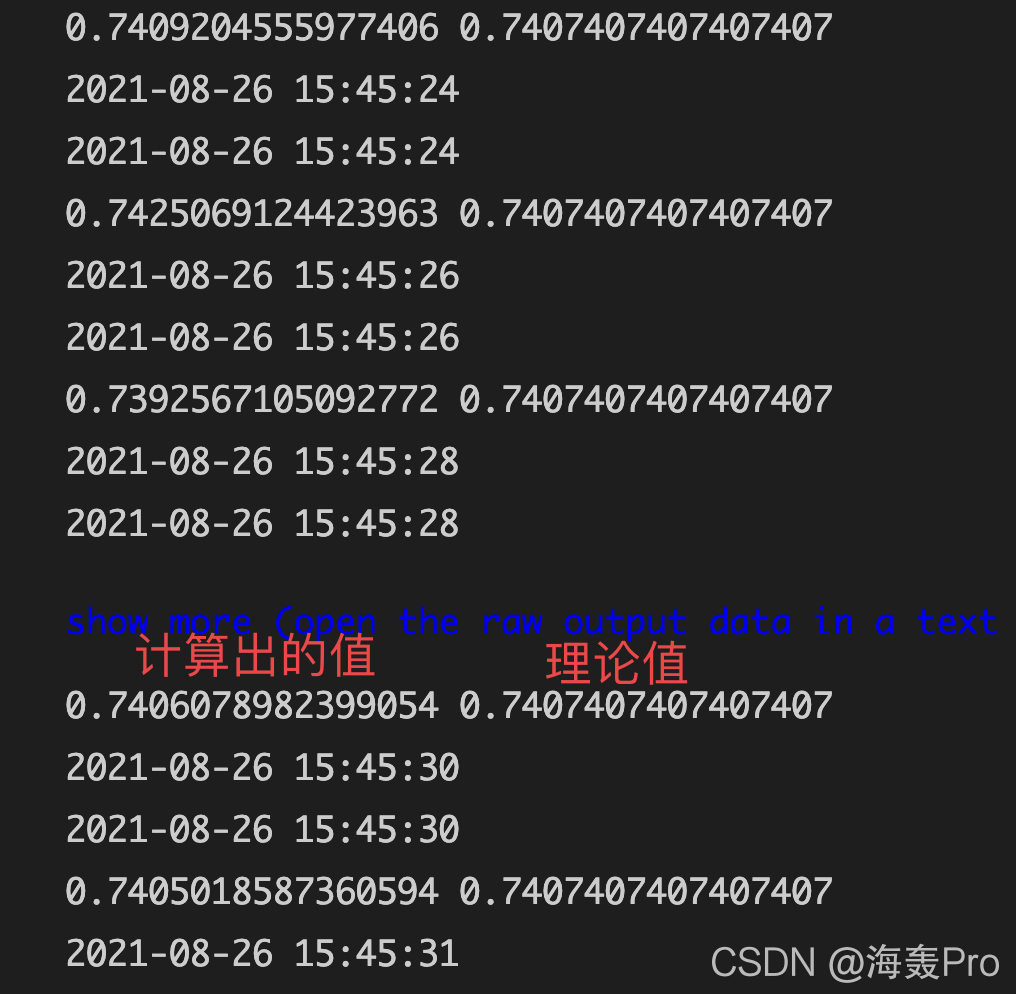
结语
参考：
https://www.bilibili.com/video/BV12h411d7Dm https://blog.csdn.net/wangyuhang124/article/details/114241080
学习来源：B站及其课堂PPT，对其中代码进行了复现
「文章仅作为学习笔记，记录从0到1的一个过程」
希望对您有所帮助，如有错误欢迎小伙伴指正～