详解蒙特卡洛方法:这些数学你搞懂了吗?

极市导读
加州大学洛杉矶分校计算机科学专业的 Ray Zhang 最近开始在自己的博客上连载介绍强化学习的文章,这些介绍文章主要基于 Richard S. Sutton 和 Andrew G. Barto 合著的《Reinforcement Learning: an Introduction》,并添加了一些示例说明。该系列文章现已介绍了赌博机问题、马尔可夫决策过程和蒙特卡洛方法。本文是对其中蒙特卡洛方法文章的编译。>>加入极市CV技术交流群,走在计算机视觉的最前沿
目录
first-visit 蒙特卡洛
探索开始
在策略:ϵ-贪婪策略
ϵ-贪婪收敛
离策略:重要度采样
离策略标记法
普通重要度采样
加权重要度采样
增量实现
其它:可感知折扣的重要度采样
其它:预奖励重要度采样
示例:Blackjack
示例:Cliff Walking
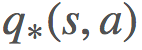 和
和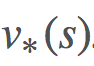 的算法。我们使用了策略迭代和价值迭代来求解最优策略。
的算法。我们使用了策略迭代和价值迭代来求解最优策略。引言
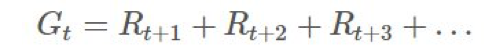
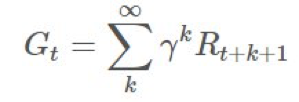
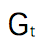 与可能的
与可能的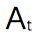 关联起来,以推导某种类型的:
关联起来,以推导某种类型的: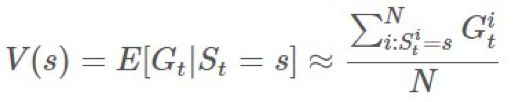
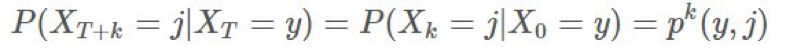
pi = init_pi()
returns = defaultdict(list)
for i in range(NUM_ITER):
episode = generate_episode(pi) # (1)
G = np.zeros(|S|)
prev_reward = 0
for (state, reward) in reversed(episode):
reward += GAMMA * prev_reward
# backing up replaces s eventually,
# so we get first-visit reward.
G[s] = reward
prev_reward = reward
for state in STATES:
returns[state].append(state)
V = { state : np.mean(ret) for state, ret in returns.items() }
蒙特卡洛动作值
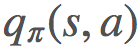 而非
而非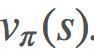 。将 G[s] 简单地改成 G[s,a] 似乎很恰当,事实也确实如此。一个显然的问题是:现在我们从 S 空间变成了 S×A 空间,这会大很多,而且我们仍然需要对其进行采样以找到每个状态-动作元组的期望回报。
。将 G[s] 简单地改成 G[s,a] 似乎很恰当,事实也确实如此。一个显然的问题是:现在我们从 S 空间变成了 S×A 空间,这会大很多,而且我们仍然需要对其进行采样以找到每个状态-动作元组的期望回报。蒙特卡洛控制
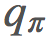 ,然后寻找一个新的 π′ 再继续。大致过程就像这样:
,然后寻找一个新的 π′ 再继续。大致过程就像这样: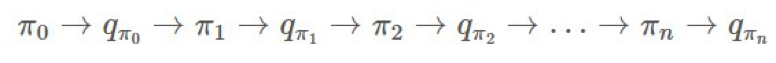
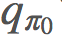 的方式类似于上面我们寻找 v 的方式。我们可以通过贝尔曼最优性方程(Bellman optimality equation)的定义改善我们的 π,简单来说就是:
的方式类似于上面我们寻找 v 的方式。我们可以通过贝尔曼最优性方程(Bellman optimality equation)的定义改善我们的 π,简单来说就是: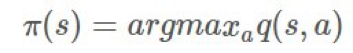
# Before (Start at some arbitrary s_0, a_0)
episode = generate_episode(pi)
# After (Start at some specific s, a)
episode = generate_episode(pi, s, a) # loop through s, a at every iteration.
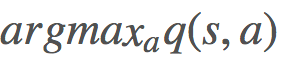 动作。
动作。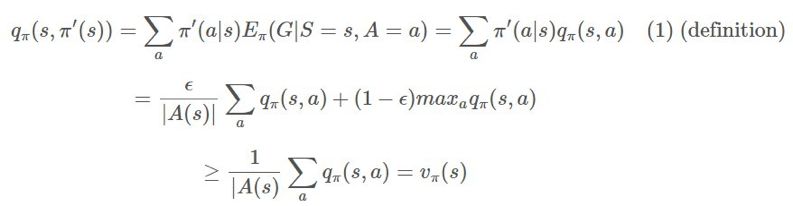
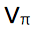 上执行单调的提升。如果我们支持所有时间步骤,那么会得到:
上执行单调的提升。如果我们支持所有时间步骤,那么会得到: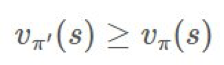
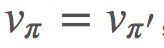 ,则由于该环境的设置,方程在随机性下是最优的。
,则由于该环境的设置,方程在随机性下是最优的。π 是我们的目标策略(target policy)。我们试图优化这个策略的期望回报。
b 是我们的行为策略(behavioral policy)。我们使用 b 来生成 π 之后会用到的数据。
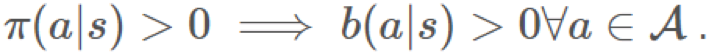 这是覆盖率(coverage)的概念。
这是覆盖率(coverage)的概念。
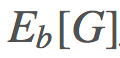 ,则
,则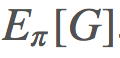 是怎样的?」换句话说,你该怎样使用你从 b 的采样得到的信息来确定来自 π 的期望结果?
是怎样的?」换句话说,你该怎样使用你从 b 的采样得到的信息来确定来自 π 的期望结果?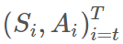 ,这个确切轨迹在给定策略 π 时的概率为:
,这个确切轨迹在给定策略 π 时的概率为: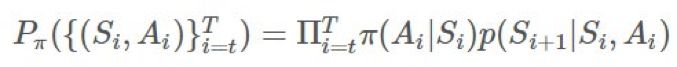
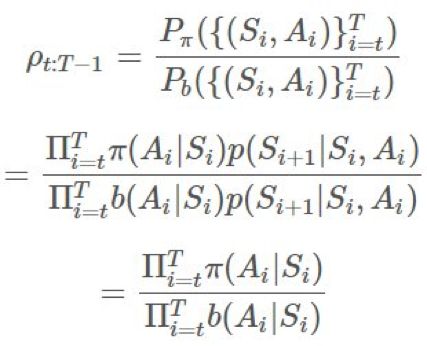
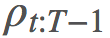 的方法,以给我们提供一个
的方法,以给我们提供一个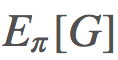 的优良估计。最基本的方法是使用被称为普通重要度采样(ordinary importance sampling)的技术。假设我们有采样得到的 N 个 episode:
的优良估计。最基本的方法是使用被称为普通重要度采样(ordinary importance sampling)的技术。假设我们有采样得到的 N 个 episode: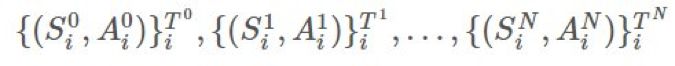
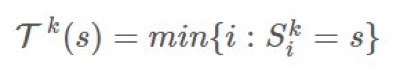
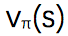 ,然后我们可以通过 first-visit 方法使用实验的均值来估计价值函数:
,然后我们可以通过 first-visit 方法使用实验的均值来估计价值函数: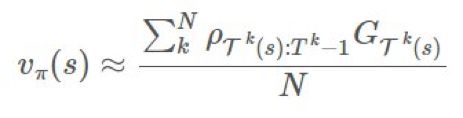
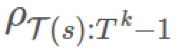 是 1000。这是个很大的比值,但绝对有可能发生。这是否意味着奖励必然会多 1000 倍?如果我们只有 1 个 episode,我们的估计就会是那样。在长期运行时,因为我们有乘法关系,所以这个比值可能要么会爆炸,要么就会消失。这对估计的目的而言是有一点问题的。
是 1000。这是个很大的比值,但绝对有可能发生。这是否意味着奖励必然会多 1000 倍?如果我们只有 1 个 episode,我们的估计就会是那样。在长期运行时,因为我们有乘法关系,所以这个比值可能要么会爆炸,要么就会消失。这对估计的目的而言是有一点问题的。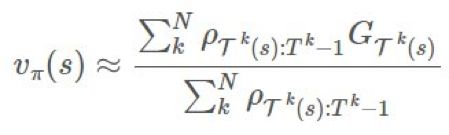
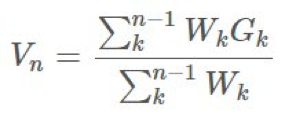
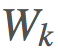 是我们的权重。
是我们的权重。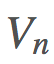 构建
构建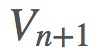 ,这是非常可行的。用
,这是非常可行的。用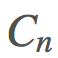 表示
表示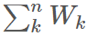 ,则我们可以保持这个运行总和的更新,即:
,则我们可以保持这个运行总和的更新,即: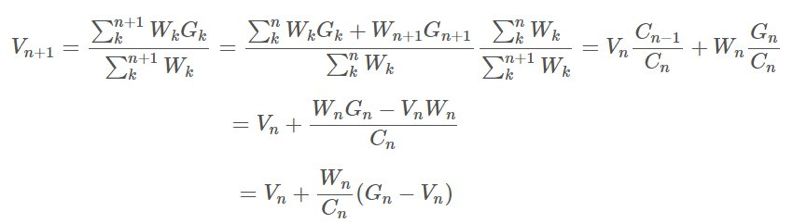
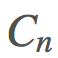 的更新规则相当明显:
的更新规则相当明显: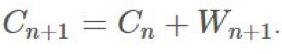
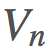 是我们的价值函数,但在我们的动作值
是我们的价值函数,但在我们的动作值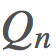 上也可以应用一个非常类似的类比。
上也可以应用一个非常类似的类比。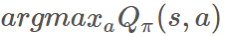 更新我们的 π。
更新我们的 π。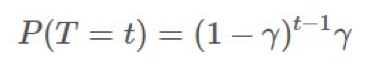
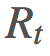 的随机数上的期望:
的随机数上的期望: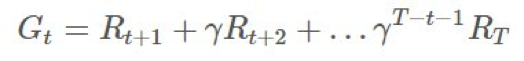
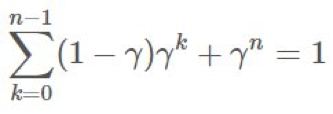
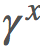 。
。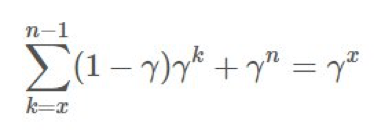
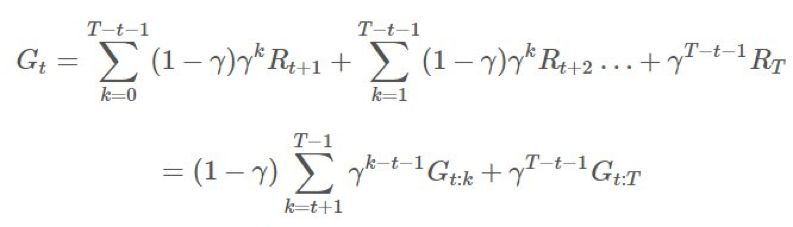
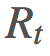 项上的等效系数为 1、γ、γ2。这意味着我们现在可将
项上的等效系数为 1、γ、γ2。这意味着我们现在可将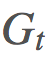 分解成不同的部分并在重要度采样比上应用折扣。
分解成不同的部分并在重要度采样比上应用折扣。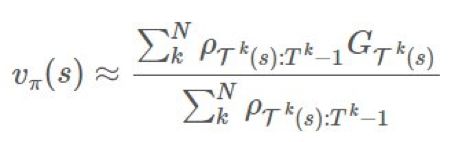
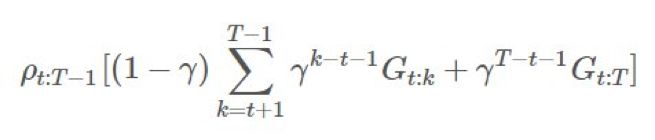
 乘上了整个轨迹的重要度比,这在「γ 是终止概率」的建模假设下是「不正确的」。直观来看,我们希望
乘上了整个轨迹的重要度比,这在「γ 是终止概率」的建模假设下是「不正确的」。直观来看,我们希望 有
有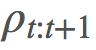 ,这是很简单的:
,这是很简单的: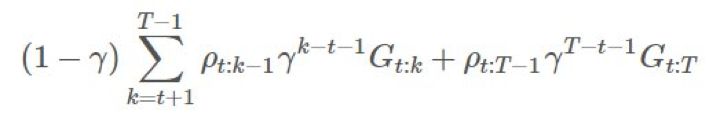
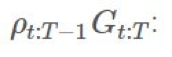 :
: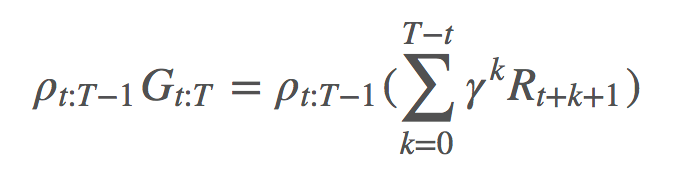
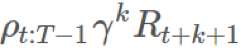 。扩展 ρ,我们可以看到:
。扩展 ρ,我们可以看到: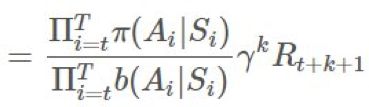
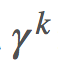 的期望:
的期望: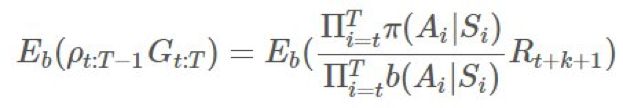
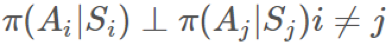 ,那么任何
,那么任何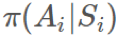 和
和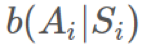 独立于
独立于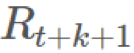 (对 b 的情况也一样)。我们可以将它们取出,然后得到:
(对 b 的情况也一样)。我们可以将它们取出,然后得到: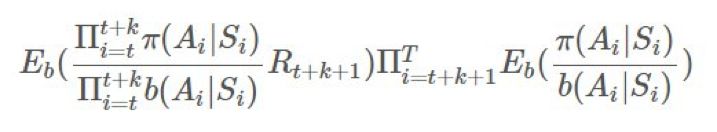
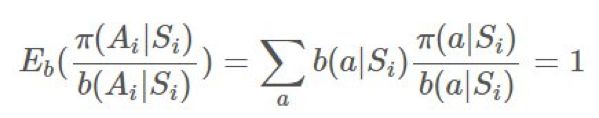
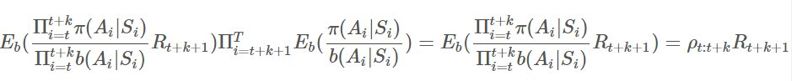
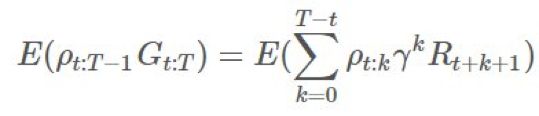
用 Python 实现的在策略模型
"""
General purpose Monte Carlo model for training on-policy methods.
"""
from copy import deepcopy
import numpy as np
class FiniteMCModel:
def __init__(self, state_space, action_space, gamma=1.0, epsilon=0.1):
"""MCModel takes in state_space and action_space (finite)
Arguments
---------
state_space: int OR list[observation], where observation is any hashable type from env's obs.
action_space: int OR list[action], where action is any hashable type from env's actions.
gamma: float, discounting factor.
epsilon: float, epsilon-greedy parameter.
If the parameter is an int, then we generate a list, and otherwise we generate a dictionary.
>>> m = FiniteMCModel(2,3,epsilon=0)
>>> m.Q
[[0, 0, 0], [0, 0, 0]]
>>> m.Q[0][1] = 1
>>> m.Q
[[0, 1, 0], [0, 0, 0]]
>>> m.pi(1, 0)
1
>>> m.pi(1, 1)
0
>>> d = m.generate_returns([(0,0,0), (0,1,1), (1,0,1)])
>>> assert(d == {(1, 0): 1, (0, 1): 2, (0, 0): 2})
>>> m.choose_action(m.pi, 1)
0
"""
self.gamma = gamma
self.epsilon = epsilon
self.Q = None
if isinstance(action_space, int):
self.action_space = np.arange(action_space)
actions = [0]*action_space
# Action representation
self._act_rep = "list"
else:
self.action_space = action_space
actions = {k:0 for k in action_space}
self._act_rep = "dict"
if isinstance(state_space, int):
self.state_space = np.arange(state_space)
self.Q = [deepcopy(actions) for _ in range(state_space)]
else:
self.state_space = state_space
self.Q = {k:deepcopy(actions) for k in state_space}
# Frequency of state/action.
self.Ql = deepcopy(self.Q)
def pi(self, action, state):
"""pi(a,s,A,V) := pi(a|s)
We take the argmax_a of Q(s,a).
q[s] = [q(s,0), q(s,1), ...]
"""
if self._act_rep == "list":
if action == np.argmax(self.Q[state]):
return 1
return 0
elif self._act_rep == "dict":
if action == max(self.Q[state], key=self.Q[state].get):
return 1
return 0
def b(self, action, state):
"""b(a,s,A) := b(a|s)
Sometimes you can only use a subset of the action space
given the state.
Randomly selects an action from a uniform distribution.
"""
return self.epsilon/len(self.action_space) + (1-self.epsilon) * self.pi(action, state)
def generate_returns(self, ep):
"""Backup on returns per time period in an epoch
Arguments
---------
ep: [(observation, action, reward)], an episode trajectory in chronological order.
"""
G = {} # return on state
C = 0 # cumulative reward
for tpl in reversed(ep):
observation, action, reward = tpl
G[(observation, action)] = C = reward + self.gamma*C
return G
def choose_action(self, policy, state):
"""Uses specified policy to select an action randomly given the state.
Arguments
---------
policy: function, can be self.pi, or self.b, or another custom policy.
state: observation of the environment.
"""
probs = [policy(a, state) for a in self.action_space]
return np.random.choice(self.action_space, p=probs)
def update_Q(self, ep):
"""Performs a action-value update.
Arguments
---------
ep: [(observation, action, reward)], an episode trajectory in chronological order.
"""
# Generate returns, return ratio
G = self.generate_returns(ep)
for s in G:
state, action = s
q = self.Q[state][action]
self.Ql[state][action] += 1
N = self.Ql[state][action]
self.Q[state][action] = q * N/(N+1) + G[s]/(N+1)
def score(self, env, policy, n_samples=1000):
"""Evaluates a specific policy with regards to the env.
Arguments
---------
env: an openai gym env, or anything that follows the api.
policy: a function, could be self.pi, self.b, etc.
"""
rewards = []
for _ in range(n_samples):
observation = env.reset()
cum_rewards = 0
while True:
action = self.choose_action(policy, observation)
observation, reward, done, _ = env.step(action)
cum_rewards += reward
if done:
rewards.append(cum_rewards)
break
return np.mean(rewards)
if __name__ == "__main__":
import doctest
doctest.testmod()
import gym
env = gym.make("Blackjack-v0")
# The typical imports
import gym
import numpy as np
import matplotlib.pyplot as plt
from mc import FiniteMCModel as MC
eps = 1000000
S = [(x, y, z) for x in range(4,22) for y in range(1,11) for z in [True,False]]
A = 2
m = MC(S, A, epsilon=1)
for i in range(1, eps+1):
ep = []
observation = env.reset()
while True:
# Choosing behavior policy
action = m.choose_action(m.b, observation)
# Run simulation
next_observation, reward, done, _ = env.step(action)
ep.append((observation, action, reward))
observation = next_observation
if done:
break
m.update_Q(ep)
# Decaying epsilon, reach optimal policy
m.epsilon = max((eps-i)/eps, 0.1)
print("Final expected returns : {}".format(m.score(env, m.pi, n_samples=10000)))
# plot a 3D wireframe like in the example mplot3d/wire3d_demo
X = np.arange(4, 21)
Y = np.arange(1, 10)
Z = np.array([np.array([m.Q[(x, y, False)][0] for x in X]) for y in Y])
X, Y = np.meshgrid(X, Y)
from mpl_toolkits.mplot3d.axes3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1)
ax.set_xlabel("Player's Hand")
ax.set_ylabel("Dealer's Hand")
ax.set_zlabel("Return")
plt.savefig("blackjackpolicy.png")
plt.show()
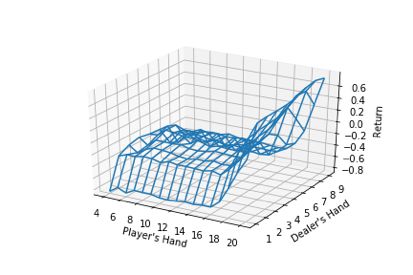
Iterations: 100/1k/10k/100k/1million.
Tested on 10k samples for expected returns.
On-policy : greedy
-0.1636
-0.1063
-0.0648
-0.0458
-0.0312
On-policy : eps-greedy with eps=0.3
-0.2152
-0.1774
-0.1248
-0.1268
-0.1148
Off-policy weighted importance sampling:
-0.2393
-0.1347
-0.1176
-0.0813
-0.072
# Before: Blackjack-v0
env = gym.make("CliffWalking-v0")
# Before: [(x, y, z) for x in range(4,22) for y in range(1,11) for z in [True,False]]
S = 4*12
# Before: 2
A = 4
总结
推荐阅读

评论
