炒股怎么炒？用动态规划啊！

hello，我是 Johngo！

股市一点红，股市一点绿！

激动的心，颤抖的手，无法控制的身子骨！

今天聊一聊股市，股价相关的问题，关系到身家的涨跌。

怎么用「动态规划」的思想去获得股市中最大利润。（LeetCode中的股价问题 手动狗头）！

说在前面

这周总算是把和大家一起刷题的「动态规划」的题目搞的差不多了。

在上一次的动态规划总结中已经把基本的解题方法四步骤以及无后效性解释的很清楚了。

而动态规划的题目中，有一类「股票」问题，很值得大家进一步分析、学习、研究。

本文就来详细说说《买卖股票的最佳时机》系列题目，看看如果我们如果在知道未来几天的股价，怎么样买卖能够达到最大的利润（有人说了，这不胡扯吗？不胡扯！股价预测、动态规划都用起来）。

《买卖股票的最佳时机》系列题目，最主要的是四个题目：分别是 LeetCode 对应的 121、122、123 和 188。

引例：只能交易一次

首先用 LeetCode121《买卖股票的最佳时机》引出。

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

因为在前后购买的时间点是没有固定的，所以可以考虑「动态规划」的思路来解决。暴力方法就不解释了。

题目中强调只能在 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票，因此，买和卖发生在不同天，不能再同一天完成。这就涉及到在某一天是否持股。

另外，由于需要求得最大的利润，所以，定义动态数组 dp 用来表示当天手中的最大利润。

注意：dp 数组表示某一天结束的时候，手中的利润。（利润指的是手中的现金数，不算已买股票的价值）。

下面按照之前说的四步走的方法进行解题。

一、动态数组定义

dp[i][j],表示持股情况为i，第 j天结束，情况下，手中的最大利润。

i代表是否持股，i=0不持股，i=1持股

j代表第j天

所以，dp 是二维数组，并且是 2 行 j 列的二维数组。

举例：股票每天的价格 prices = [7, 1, 5, 3, 6, 4]

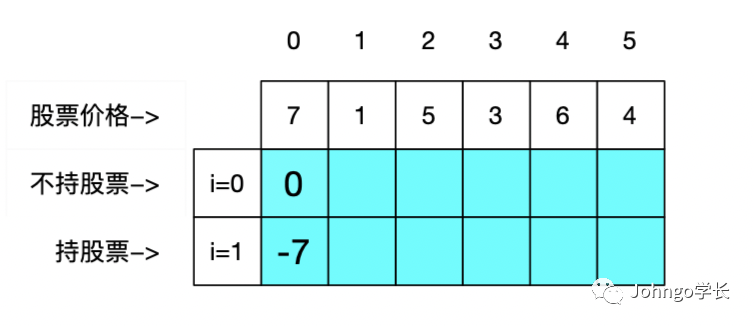
二、状态转移方程

dp[0][j]：表示该天不持股

很容易想到，如果今天不持股，那么昨天可能持股也可能不持股。分别讨论:

① 今天不持股，并且在昨天也不持股的情况下，手中的利润是不变的：

dp[0][j] = dp[0][j-1]

② 今天不持股，而在昨天持股的情况下，手中的利润一定是增加的（卖掉股票）：

dp[0][j] = dp[1][j-1] + prices[j]

所以，今天的最大价值是：dp[0][j] = max(dp[0][j-1], dp[1][j-1] + prices[j])

dp[1][j]：表示该天持股

① 今天持股，并且在昨天也持股的情况下，手中的利润是不变的：

dp[1][j] = dp[1][j-1]

② 今天持股，而在昨天不持股的情况下，手中的利润一定是减少的，因为进行了买操作：

另外，由于本题规定只发生买卖一次，所以，在发生买操作的时候，直接就是减去当天的股价。

dp[1][j] = -prices[j]

所以，今天的最大价值是：dp[1][j] = max(dp[1][j-1], -prices[j])

三、初始化

如果第 0 天不发生买入操作：dp[0][0] = 0

如果第 0 天发生了买入操作：dp[1][0] = -prices[0]

下面，用一个长图进行一步一步把上述的二维数组填满：

因为要取最优利润值。所以，卖掉股票后才能有最大利润，除非，一次都没有交易。

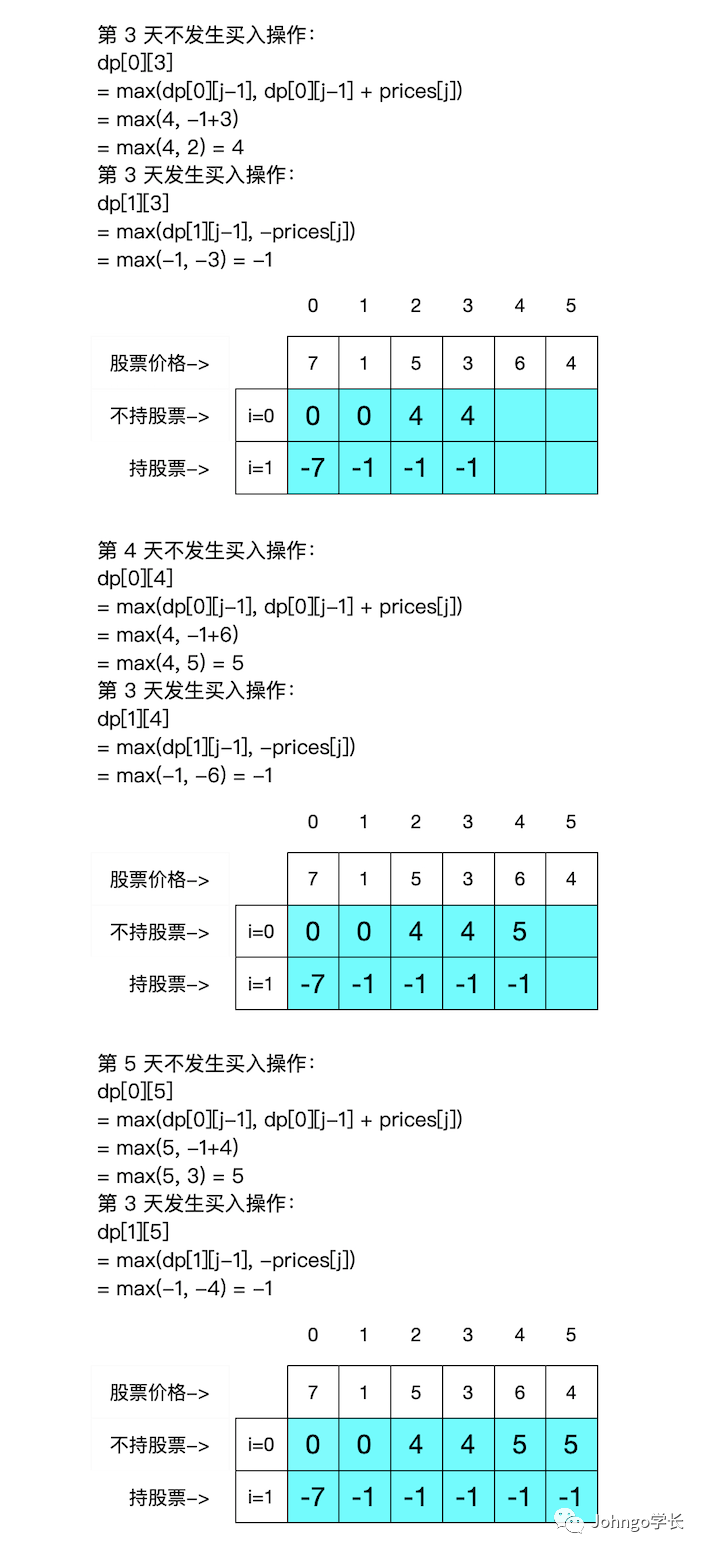
故：max_profit = dp[0][-1]

看下核心代码：

def maxProfit(self, prices):
    size = len(prices)
    if size == 0 or size == 1:
        return 0
    # 定义动态数组
    dp = [[0 for _ in range(size)] for _ in range(2)]
    # 初始化动态数组
    dp[0][0] = 0
    dp[1][0] = -prices[0]
    # 动态方程
    for j in range(1, size):
        dp[0][j] = max(dp[0][j - 1], dp[1][j - 1] + prices[j])
        dp[1][j] = max(dp[1][j - 1], -prices[j])
    return dp[0][-1]

是不是看完图中描述和代码后，这个题目的思路就很明显并且很通畅了。

别着急，咱们再看看优化项，除了思路的清晰通畅，看了下面的优化点思路会更加觉得优秀！（呃。。。）

四、优化

在进行每一步计算的过程中可以发现，在每一天的计算中，只与前一天的计算结果有关系，与再之前的数据是没有关系的。

比如，在计算第 3 天的利润时，只与第 2 天的两个状态下的值有关系。

所以，只需要保留两个变量就可以将空间方面进行优化。可以动手按照上述思路画一下，很清晰的思路就出来了。

空间方面的优化代码：

def maxProfit_opt(self, prices):
    size = len(prices)
    if size == 0 or size == 1:
        return 0
    dp1 = 0
    dp2 = -prices[0]
    for j in range(1, size):
        tmp1 = max(dp1, dp2+prices[j])
        tmp2 = max(dp2, -prices[j])
        dp1, dp2 = tmp1, tmp2
    return dp1

无限制买卖

上面 LeetCode121 题目限制了在给定的范围内，只能进行一次买卖。

下面的 LeetCode122 无限制进行买卖，进行求解最大利润。

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

近乎同样的解决逻辑，只是在进行买入股票的时候需要考虑之前的利润状态，上一个题目买入股票不需要考虑之前的利润状态，因为只进行一次买卖。

还是详细的来说说，每个步骤具体怎么状态转移。

一、动态数组定义

dp[i][j],表示持股情况为i，第 j天结束，情况下，手中的最大利润。

i代表是否持股，i=0不持股，i=1持股

j代表第j天

所以，dp 是依然是二维数组，并且是 2 行 j 列的二维数组。

举例：股票每天的价格 prices = [7, 1, 5, 3, 6, 4]

二、状态转移方程

dp[0][j]：表示该天不持股

很容易想到，如果今天不持股，那么昨天可能持股也可能不持股。分别讨论:

① 今天不持股，并且在昨天也不持股的情况下，手中的利润是不变的：

dp[0][j] = dp[0][j-1]

② 今天不持股，而在昨天持股的情况下，手中的利润一定是增加的：

dp[0][j] = dp[1][j-1] + prices[j]

今天的最大价值是：dp[0][j] = max(dp[0][j-1], dp[1][j-1] + prices[j])

dp[1][j]：表示该天持股

① 今天持股，并且在昨天也持股的情况下，手中的利润是不变的：

dp[1][j] = dp[1][j-1]

② 今天持股，而在昨天不持股的情况下，手中的利润一定是减少的，因为进行了买操作：

因为无限次买卖。所以，在发生买操作的时候，需要将之前的利润状态减去当天的股价。

dp[1][j] = dp[0][j-1] - prices[j]

所以，今天的最大价值是：dp[1][j] = max(dp[1][j-1], dp[0][j-1] - prices[j])

三、初始化

如果第 0 天不发生买入操作：dp[0][0] = 0

如果第 0 天发生买入操作：dp[1][0] = -prices[0]

下面，依然用一个长图进行一步一步把上述的二维数组填满：

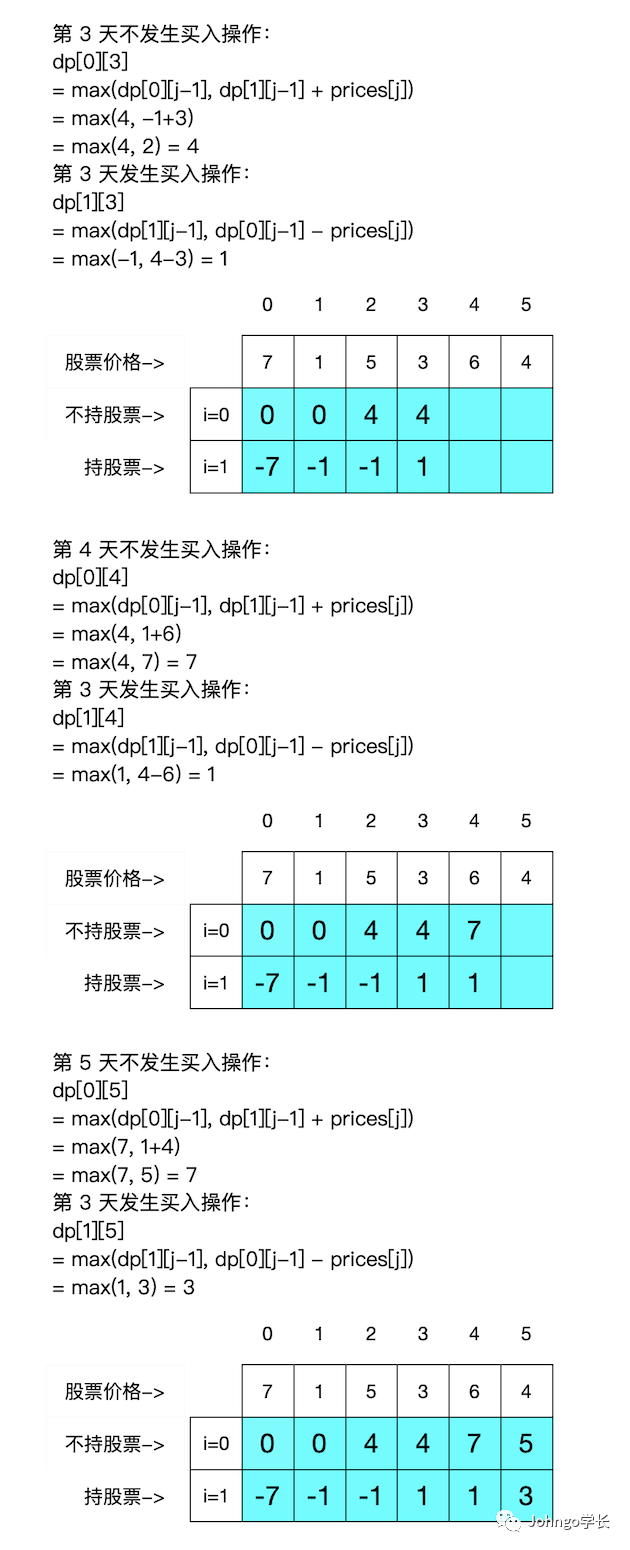
最后拿到 dp[0]的最后一个元素就是最大利润值，因为不持股手中的利润就是多的情况。

即：max_profit = dp[0][-1]

核心代码：

def maxProfit(self, prices):
    size = len(prices)
    if size == 0 or size == 1:
        return 0
    # 定义动态数组
    dp = [[0 for _ in range(size)] for _ in range(2)]
    # 初始化动态数组
    dp[0][0] = 0
    dp[1][0] = -prices[0]
    # 动态方程
    for j in range(1, size):
        dp[0][j] = max(dp[0][j - 1], dp[1][j - 1] + prices[j])
        dp[1][j] = max(dp[1][j - 1], dp[0][j - 1] - prices[j])
    print(dp)
    return dp[0][-1]

四、优化

同样的优化方案，还是从空间的角度进行优化。

同样很显然的，每一天利润值计算无论是买股票还是卖股票，都是只与前一天有关系。

因此，只需要设置两个值（dp1、dp2）存放持有和不持有股票的最大利润值，就可以简化空间计算。

核心代码：

def maxProfit_opt(self, prices):

    size = len(prices)
    if size == 0 or size == 1:
        return 0
    # 初始化动态数组
    dp1 = 0
    dp2 = -prices[0]
    for j in range(1, size):
        tmp1 = max(dp1, dp2 + prices[j])
        tmp2 = max(dp2, dp1 - prices[j])
        dp1, dp2 = tmp1, tmp2
    return dp1

以上，在 LeetCode 中都属于 easy 模式的题目。

如果说，在一段时间内，只允许交易固定次数的时候，该怎么做？

比如，在 6 天时间内，允许交易 2 次，求最大利润？或者交易 k 次，求最大利润？

交易 2 次，最大利润？

下面的 LeetCode123 规定只进行 2 次买卖，进行求解最大利润。

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

还有一点注意，之前的题目强调，同一天不能既买又卖，但是当前的问题没有强调这一点，是可以在同一天进行买卖的。

思路和之前的题目还是有一点区别的， 建议一定细致读每一个字。

下面详细的来说说，每个步骤具体怎么状态转移。

一、动态数组定义

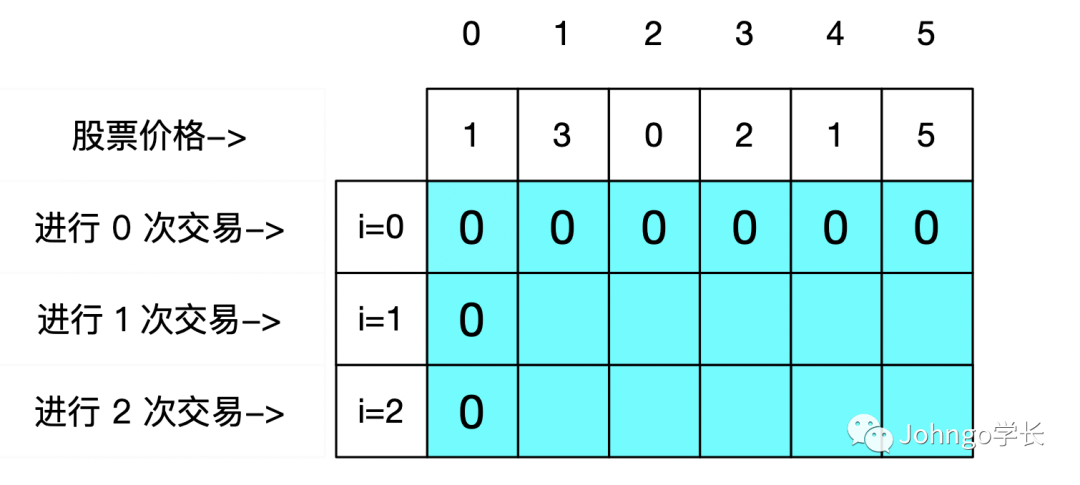
dp[i][j]，代表进行 i次交易，在第 j 天的时候的最大利润。

i代表交易次数

j代表天数

举例：股票每天的价格 prices = [1, 3, 0, 2, 1, 5]

根据案例，定义 dp 数组为 3 行 6 列。

二、状态转移方程

和之前的有点不一样

动态方程：dp[i][j]=max{dp[i][j-1], max{prices[i]-prices[n]+dp[i-1][n]}}, n=0,1,…,j-1

看起来很复杂，公式复杂，其实思路还是比较简单。

不要着急，也不要被吓退，后面会每一步将上述动态数组填满，填满之后发现真的比较简单。

三、初始化

dp[0]=0 ：如果一直进行 0 次交易。那么，无论到第几天，利润都为 0

dp[1][0]：第 0 天，进行 1 次交易，无论是买、卖还是买+卖都进行，最大利润必为 0

dp[2][0]：第 0 天，进行 2 次交易，无论是买、卖还是买+卖都进行，最大利润还为 0

初始化之后，就可以将上述二维数组填满，即可清晰看到每一步的计算过程。

【建议查看高清图片或者直接到 github 进行读取】

注意，以上红框中也是要取最大值，对应动态方程中的第二个max。下面所有图示均符合此规律。

上述步骤中，只填写了第 i=1 这一行。

最大利润值，要么取前一天的数据，要么就是公式中的计算逻辑。取其最大值。

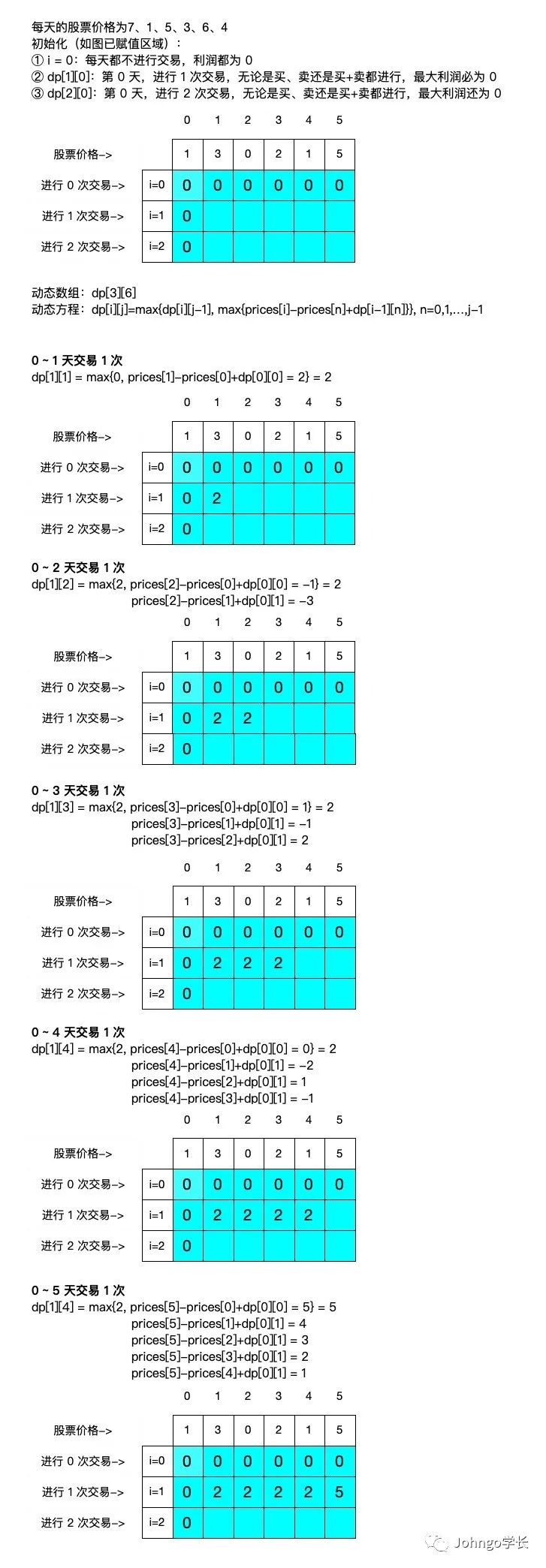
下面再把第 i=2 这一行填完，大家的思路会更加清晰起来。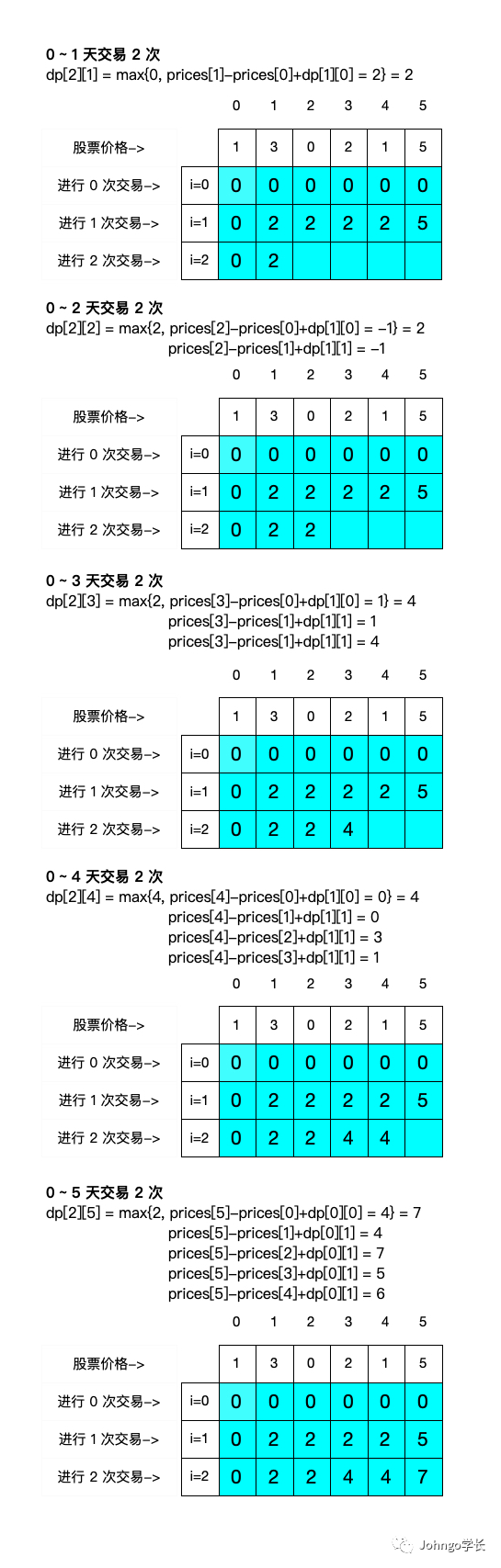

这一顿操作，我简直差点要放弃了。

就按照上述思路，代码下来，发现执行超时，又一次差点放弃解答。

也不可谓难度为困难，而困难点就在这里。

至此，必须要进行优化，将时间复杂度降低下来。一般来说，动态规划的题目是将空间复杂度降低，时间复杂度降低的题目相对比较少一点。

四、优化

从上面图中，很容易发现一点重复计算的部分。

下面就拿出来最后 2 个步骤的其中一些公式对照：

prices[4]-prices[0]+dp[0][0] prices[4]-prices[1]+dp[0][1] prices[4]-prices[2]+dp[0][1] prices[4]-prices[3]+dp[0][1]

和

prices[5]-prices[0]+dp[0][0] prices[5]-prices[1]+dp[0][1] prices[5]-prices[2]+dp[0][1] prices[5]-prices[3]+dp[0][1] prices[5]-prices[4]+dp[0][1]

可以明显看出来，上述被标注的部分又是重复的计算。

最左侧一列都是当前的股票价格，也是不变的。

那么，这个时候就可以使用一个变量max_profit来进行记录右侧被标记部分的最大值。

将之前的动态方程：

dp[i][j]=max{dp[i][j-1], max{prices[i]-prices[n]+dp[i-1][n]}}, n=0,1,…,j-1

改为：

dp[i][j]=max{dp[i][j-1], prices[j]+max_profit}

其中，max_profilt=max{dp[i-1][j]-prices[j], max_profit}

这里这里这里很重要，一定画图理解。

也许就是该题目难度被设置为“困难”的地方！

看代码，很简单的实现：

def maxProfit(self, prices):
    """
    使用动态规划解决: 最多完成 2 次交易
    """
    size = len(prices)
    if size == 0:
        return 0
    dp = [[0 for _ in range(size)] for _ in range(3)]
    print(dp)

    for i in range(1, 3):
        # 每一次交易的最大利润
        max_profit = -prices[0]
        for j in range(1, size):
            dp[i][j] = max(dp[i][j-1], max_profit + prices[j])
            max_profit = max(max_profit, dp[i-1][j] - prices[j])
    print(dp)
    return dp[-1][-1]

这样就完美解决了！

交易多次，最大利润？

LeetCode123 规定最多交易 2 次，下面再上升一个难度。

在 LeetCode188. 买卖股票的最佳时机 IV，最多可以完成 k 笔交易，求最大的利润。

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

如果 LeetCode123 题目理解清楚的话，这个题目很快就可以解决了。

上一题规定最多交易 2 次，改题目最多交易 k 次。即：把 2 次的逻辑换为 k 次逻辑，就可以解决了。

直接看代码吧，和上一个题很类似：

def maxProfit(self, k, prices):

    size = len(prices)
    if size == 0:
        return 0
    dp = [[0 for _ in range(size)] for _ in range(k+1)]
    print(dp)

    for i in range(1, k+1):
        # 每一次交易的最大利润
        max_profit = -prices[0]
        for j in range(1, size):
            dp[i][j] = max(dp[i][j-1], max_profit + prices[j])
            max_profit = max(max_profit, dp[i-1][j] - prices[j])
    print(dp)
    return dp[-1][-1]

看出来不一样的地方了吧，就是在之前逻辑设置为 2 的地方，在本地改为 k 次即可！

注意：之前是 range(1, 3)代表 1 和 2， range(1,k+1) 代表 1,2,3,...,k

以上！

《买卖股票的最佳时机》系列题目详细的进行了解释，后面还有其他的股票相关题目，但基本是基于今天文章的思路进行解决的。

刷题计划已经进行了有一段时间，需要一起来搞的，加我微信，我拉你进群哈！

也可围观我的朋友圈不定时分享有关互联网各种干货和趣事，或者还有许多不痛不痒的事情，总之乱七八糟吧哈！

开心最好。

坑位紧缺，票圈开业期待大家的光临！