作者：钟阳扬

审校：陈之炎

图(Graph)是一种数据结构, 能够很自然地建模现实场景中一组实体之间的复杂关系。在真实世界中，很多数据往往以图的形式出现, 例如社交网络、电商购物、蛋白质相互作用关系等。因此，近些年来使用智能化方式来建模分析图结构的研究越来越受到关注, 其中基于深度学习的图建模方法的图神经网络(Graph Neural Network, GNN), 因其出色的性能已广泛应用于社会科学、自然科学等多个领域。

基本概念

1.1 图的基本概念

通常使用G=(V, E)来表示图，其中V表示节点的集合、E表示边的集合。对于两个相邻节点u, v, 使用e=(u,v)表示这两个节点之间的边。两个节点之间边既可能是有向，也可能无向。若有向，则称之有向图(Directed Graph), 反之，称之为无向图(Undirected Graph)。

1.2 图的表示

在图神经网络中，常见的表示方法有邻接矩阵、度矩阵、拉普拉斯矩阵等。

1)邻接矩阵(Adjacency Matrix)

用于表示图中节点之间的关系，对于n个节点的简单图，有邻接矩阵: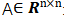

 

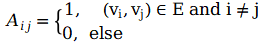
2)度矩阵(Degree Matrix)

节点的度(Degree)表示与该节点相连的边的个数，记作d(v)。对于n个节点的简单图G=(V, E)，其度矩阵D为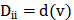，也是一个对角矩阵。

3）拉普拉斯矩阵 (Laplacian Matrix)

对于n个节点的简单图G=(V, E)，其拉普拉斯矩阵定义为L=D-A，其中D、A为上面提到过的度矩阵和邻接矩阵. 将其归一化后有 。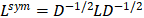

1.3 图神经网络基本概念

图神经网络(GNN)最早由Marco Gori [1]、Franco Scarselli [2,3]等人提出，他们将神经网络方法拓展到了图数据计算领域。在Scarselli论文中典型的图如图1所示：

 图1 典型的图神经网络

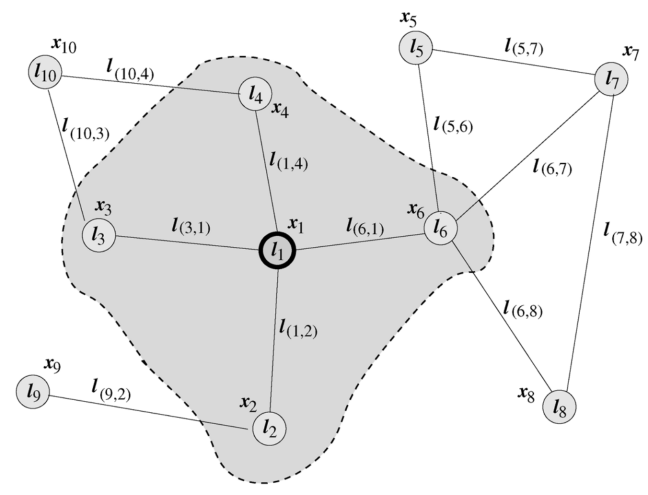
为了根据输入节点邻居信息更新节点状态，将局部转移函数f定义为循环递归函数的形式, 每个节点以周围邻居节点和相连的边作为来源信息来更新自身的表达h。为了得到节点的输出o, 引入局部输出函数g。因此，有以下定义：

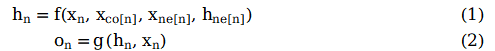
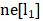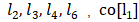其中x表示节点投中, h表示节点隐状态，ne[n]表示表示节点n的邻居节点集合，co[n]表示节点n的邻接边的集合。以图1的L1节点为例，X1是其输入特征,包含节点 , 包含边。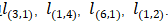

将所有局部转移函数f堆叠起来, 有：

其中F是全局转移函数(Global Transition Function), G是全局输出函数(Global Output Function)。

根据巴拿赫不动点定理[4]，假设公式(3)的F是压缩映射，那么不动点H的值就可以唯一确定，根据以下方式迭代求解:

基于不动点定理，对于任意初始值，GNN会按照公式(5)收敛到公式(3)描述的解。

经典模型

2.1 GCN-开山之作

2017年，Thomas N. Kipf等人提出GCN[5]. 其结构如图2所示：

 图2  Thomas N. Kipf等人提出GCN

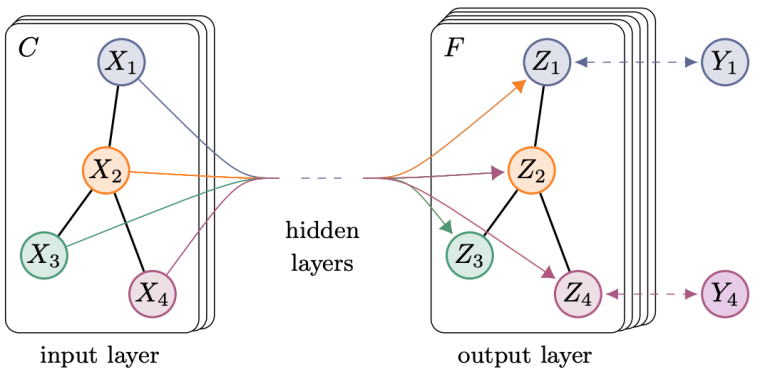
假设需要构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式如下所示：

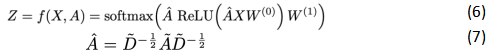
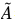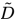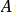其中W0表示第一层的权重矩阵，W1表示第二层的权重矩阵，X为节点特征，等于邻接矩阵A和单位矩阵相加，为的度矩阵。

从上面的正向传播公式和示意图来看，GCN好像跟基础GNN没什么区别。接下里给出GCN的传递公式(8)：

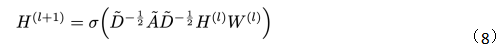
观察一下归一化的矩阵与特征向量矩阵的乘积：

来源：

https://www.zhihu.com/question/426784258

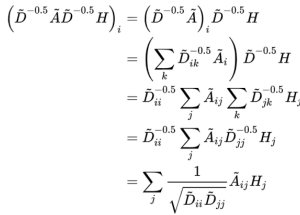
可以发现，GCN引入度矩阵D用于对邻接矩阵的归一化后，层间传播将不再单单地对领域节特征点取平均，它不仅考虑了节点i对度，也考虑了邻接节点j的度，对于度数较大的节点，它在聚合时贡献地会更少。

文章[5]通过实验证明GCN性能出色，GCN即使不训练，提取出来的特征已经非常优秀,作者做了一个实验，使用俱乐部关系网络数据，如图3所示：

图3  GCN在空间上自动聚类从上图可以发现，使用随机初始化的GCN进行特征提取，经过GCN的提取出的embedding，已经在空间上自动聚类了。

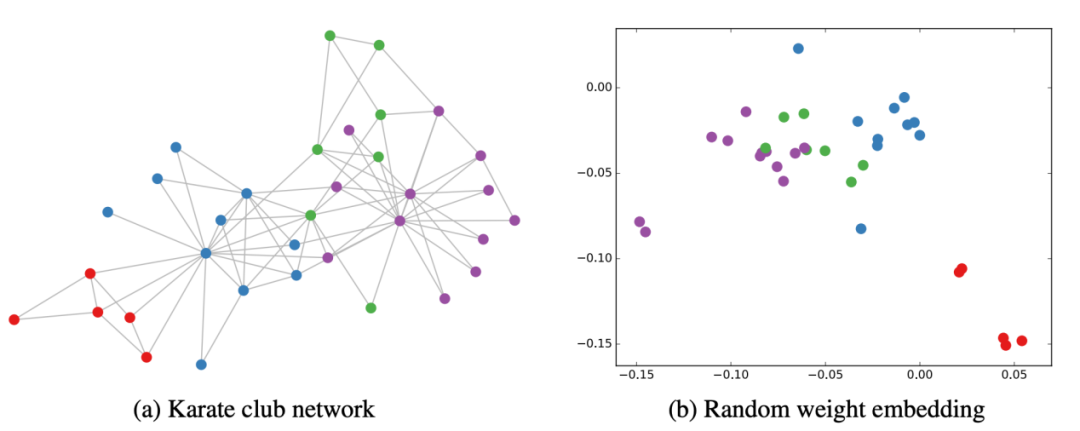
2.2 GAT - attention机制

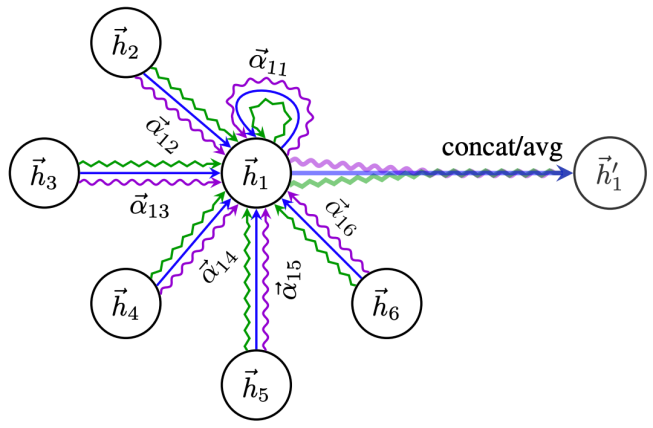
GAT[6]是典型的基于注意力机制的图神经网络。图注意网络结构如图4所示,节点i，j的特征作为输出，计算两节点之间的注意力权重。

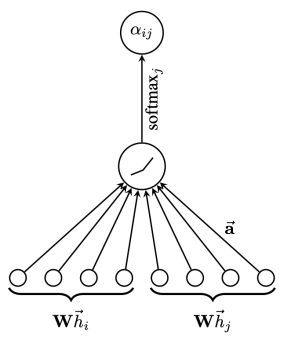
图4 图注意网络结构

对于节点i,j 的注意力系数（Attention Coefficients）计算方式为：

其中W是一个共享参数的线性映射对于节点特征的增维，h就是节点的特征，a(W，W)可以表示两个向量内积计算相似度。再经过softmax得到注意力权重：

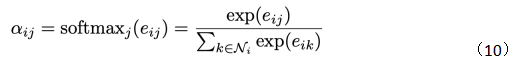
那么有如下注意力权重计算公式：

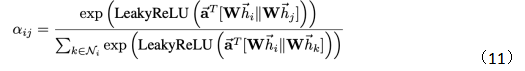
其中Ni表示节点i的邻居节点，||表示特征拼接。

最终节点的输出如下公式所示，很好理解，就是给邻居节点分配不同的权重来聚合信息。

在文章[6]中，作者还引入了多头注意力，结构如图5所示，公式如（13）所示：

 图5 多头注意力机制结构

       

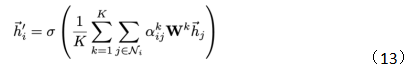
多头注意力本质是引入并行的几个独立的注意力机制，可以提取信息中的多重含义，防止过拟合。

2.3 GraphSAGE -归纳式学习框架

提到GraphSAGE[7]模型, 不得不又提到GCN，我们回顾一下GCN的迭代公式：

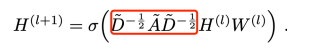
图中红框位置所做的操作可以简单理解为对邻接矩阵A的归一化变换，去掉该部分会发现剩下的结构等同于深度神经网络，加上红色部分后，通过矩阵乘法实际上所做的就是将节点与节点相邻节点特征信息进行相加。

GraphSAGE在特征聚合方式上与GCN简单相加不同，GraphSAGE支持max-pooling、LSTM、mean等聚合方式。另外，GraphSAGE与GCN的最大不同点在于，GCN是直推式方法，即所有节点都在图中，对于新出现的节点无法处理。GraphSAGE是归纳式，对于没见过的节点也能生成embedding。

GraphSAGE的传播方法如图6所示：

图6 GraphSAGE的传播方法

可以看到对于图G中的某个节点v，需要聚合k层信息，那么先有个对层数遍历的for循环，第二层循环便是遍历节点v的邻居节点，然后通过聚合函数AGGEGATE(可以是mean、max、LSTM或者其他)来聚合k-1层的邻居节点信息，得到聚合后的k层邻居节点信息，然后将聚合后的k层邻居节点信息与k-1层节点v的信息进行拼接，然后通过权重参数W进行计算得到K层关于节点v的信息。

直观一点，可以看看下面这幅图：

 图7 图节点的传播方式

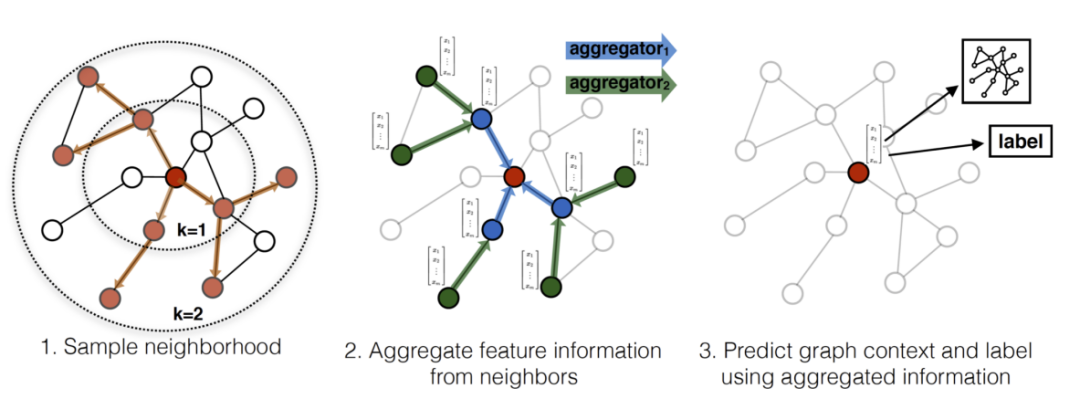
以为红色节点为目标节点，在一次步骤中，对红色节点的一阶邻居和二阶段邻居做随机采样。然后通过聚合策略，把节点的特征信息从二阶邻居聚合到目标节点上，然后用更新后的目标节点的表征可以应用到不同需求的任务上。

结论

综上所述，GraphSAGE相对于GCN可以避免需要一次性加载整张网络、能够灵活设计聚合方式、具备Transductive性质。可以适配测试集的节点变化，不需要像GCN一样会因为节点变化造成拉普拉斯矩阵变化导致需要重新训练模型。

参考文献

[1] M. Gori, G. Monfardini and F. Scarselli, "A new model for learning in graph domains," Proceedings. 2005 IEEE International Joint Conference on Neural Networks, 2005., 2005, pp. 729-734 vol. 2, doi: 10.1109/IJCNN.2005.1555942.

[2] Scarselli F , Tsoi A C ,  Gori M , et al. Graphical-Based Learning Environments for Pattern Recognition[J]. DBLP, 2004.

[3]Franco,Scarselli,Marco,Gori,AhChung,Tsoi,Markus,Hagenbuchner,Gabriele,Monfardini.The graph neural network model.[J].IEEE transactions on neural networks,2009,20(1):61-80.DOI:10.1109/TNN.2008.2005605.

[4]MA Khamsi, WA Kirk. An Introduction to Metric Spaces and Fixed Point Theory. 2011.

[5] Kipf T N , Welling M . Semi-Supervised Classification with Graph Convolutional Networks[J].  2016.

[6] Velikovi P , Cucurull G ,  Casanova A , et al. Graph Attention Networks[J].  2017.

[7] W. Hamilton, Z. Ying and J. Leskovec, "Inductive representation learning on large graphs" in Advances in Neural Information Processing Systems, pp. 1025-1035, 2017.

作者简介

钟阳扬，数据派研究部志愿者，硕士毕业于东北大学，主要研究方向为计算机视觉、图神经网络等。

编辑：于腾凯

校对：林亦霖

>>更多阅读

• 数据分析师必需具备的10种分析思维
  

• 网易用户体验研究中心：游戏交易网络的洞察分析
  

• 为什么大多数据分析失败的原因分析及解决策略