GNN大有可为,从这篇开始学以致用
作者:十方
说到GNN,各位炼丹师会想到哪些算法呢?不管想到哪些算法,我们真正用到过哪些呢?确实我们可能都看过GNN相关论文,但是还是缺乏实战经验的.特别是对于推荐系统而言,我们又该如何应用这些模型呢?下面我们就从DeepWalk这篇论文开始,先讲原理,再讲实战,最后讲应用.

GNN相关背景知识

GNN的本质,是要学习网络中每个节点的表达的,这些潜在的表达对图中每个节点的“社交”关系进行了编码,把离散值的节点编码成稠密向量,后续可用于分类回归,或者作为下游任务的特征.Deepwalk充分利用了随机游走提取的“句子”,去学习句子中每个单词的表达.Deepwalk原文就提到了在数据稀疏的情况下可以把F1-scores提升10%,在一些实验中,能够用更少的训练数据获得了更好的效果.看下图的例子:
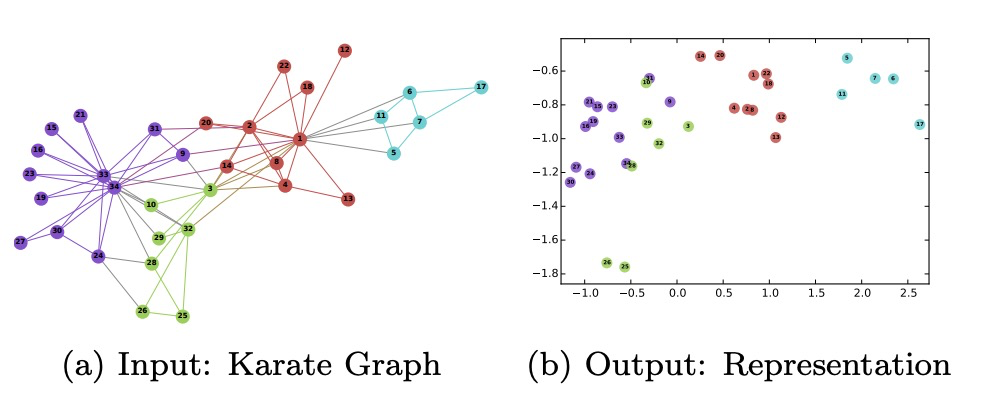

Deepwalk

问题定义:先把问题定义为给社交网络中的每个节点进行分类,图可以表达为G=<V,E>,V就是图上所有节点,E是所有边.有一部分有label的数据GL=(V,E,X,Y),X就是节点的特征,Y就是分类的label.在传统机器学习算法中,我们都是直接学习(X,Y),并没有充分利用节点间的依赖关系.Deepwalk可以捕捉图上的拓扑关系,通过无监督方法学习每个节点的特征,学到的图特征和标签的分布是相互独立的.
随机游走:选定一个根节点,“随机”走出一条路径,基于相邻的节点必然相似,我们就可以用这种策略去挖掘网络的社群信息.随机游走很方便并行,可以同时提取一张图上各个部分的信息.即使图有小的改动,这些路径也不需要重新计算.和word的出现频率类似,通过随机游走得到的节点访问频率都符合幂律分布,所以我们就可以用NLP相关方法对随机游走结果做相似处理,如下图所示:

所以在随机游走后,我们只需要通过下公式,学习节点向量即可:
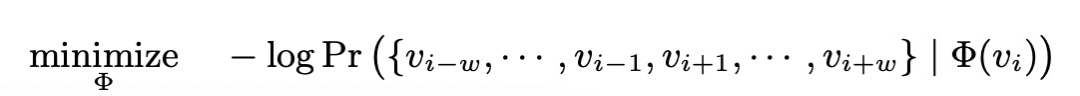
该公式就是skip-gram,通过某个节点学习它左右的节点.我们都知道skip-gram用于文本时的语料库就是一个个句子,现在我们提取图的句子.如下所示:

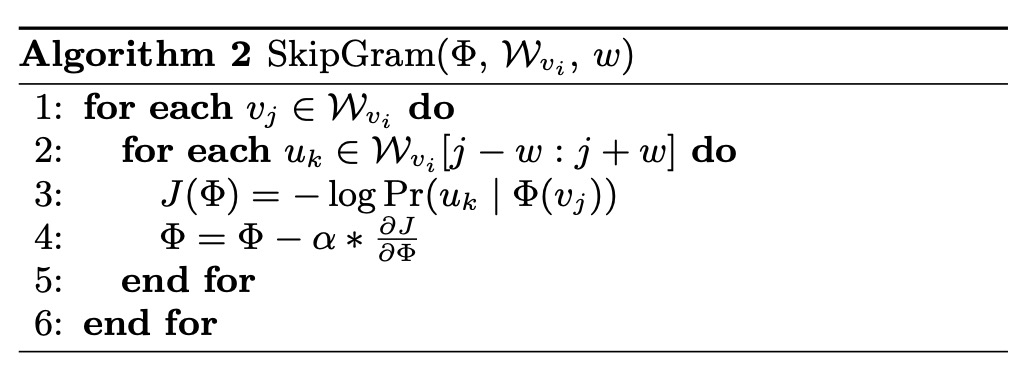
算法很简单,把所有节点顺序打乱(加速收敛),然后遍历这些节点随机游走出序列,再通过skipgram算法去拟合每个节点的向量.如此反复.注:这里的随机是均匀分布去随机.当然有些图会有些“副产物”,比如用户浏览网页的顺序,可以直接输入到模型.
接下来我们看下deepwalks的核心代码:
# 代码来源# https://github.com/phanein/deepwalk# Random walkwith open(f, 'w') as fout:for walk in graph.build_deepwalk_corpus_iter(G=G, # 图num_paths=num_paths, # 路径数path_length=path_length, # 路径长度alpha=alpha, #rand=rand): #fout.write(u"{}\n".format(u" ".join(v for v in walk)))class Graph(defaultdict):"""Efficient basic implementation of nx这里我们看到,该类继承defaultdict,图其实可以简单的表示为dict,key为节点,value为与之相连的节点"""def __init__(self):super(Graph, self).__init__(list)def nodes(self):return self.keys()def adjacency_iter(self):return self.iteritems()def subgraph(self, nodes={}):# 提取子图subgraph = Graph()for n in nodes:if n in self:subgraph[n] =return subgraphdef make_undirected(self):#因为是无向图,所以v in self[u]并且 u in self[v]t0 = time()for v in list(self):for other in self[v]:if v != other:self[other].append(v)t1 = time()logger.info('make_directed: added missing edges {}s'.format(t1-t0))self.make_consistent()return selfdef make_consistent(self):# 去重t0 = time()for k in iterkeys(self):self[k] = list(sorted(set(self[k])))t1 = time()logger.info('make_consistent: made consistent in {}s'.format(t1-t0))self.remove_self_loops()return selfdef remove_self_loops(self):# 自已不会与自己有连接removed = 0t0 = time()for x in self:if x in self[x]:self[x].remove(x)removed += 1t1 = time()logger.info('remove_self_loops: removed {} loops in {}s'.format(removed, (t1-t0)))return selfdef check_self_loops(self):for x in self:for y in self[x]:if x == y:return Truereturn Falsedef has_edge(self, v1, v2):# 两个节点是否有边if v2 in self[v1] or v1 in self[v2]:return Truereturn Falsedef degree(self, nodes=None):# 节点的度数if isinstance(nodes, Iterable):return {v:len(self[v]) for v in nodes}else:return len(self[nodes])def order(self):"Returns the number of nodes in the graph"return len(self)def number_of_edges(self):# 图中边的数量"Returns the number of nodes in the graph"return sum([self.degree(x) for x in self.keys()])/2def number_of_nodes(self):# 图中结点数量"Returns the number of nodes in the graph"return self.order()# 核心代码def random_walk(self, path_length, alpha=0, rand=random.Random(), start=None):""" Returns a truncated random walk.path_length: Length of the random walk.alpha: probability of restarts.start: the start node of the random walk."""G = selfif start:path =else:# Sampling is uniform w.r.t V, and not w.r.t Epath =while len(path) < path_length:cur = path[-1]if len(G[cur]) > 0:if rand.random() >= alpha:path.append(rand.choice(G[cur])) # 相邻节点随机选else:path.append(path[0]) # 有一定概率选择回到起点else:breakreturn# TODO add build_walks in heredef build_deepwalk_corpus(G, num_paths, path_length, alpha=0,rand=random.Random(0)):walks =nodes = list(G.nodes())# 这里和上面论文算法流程对应for cnt in range(num_paths): # 外循环,相当于要迭代多少epochrand.shuffle(nodes) # 打乱nodes顺序,加速收敛for node in nodes: # 每个node都会产生一条路径walks.append(G.random_walk(path_length, rand=rand, alpha=alpha, start=node))return walksdef build_deepwalk_corpus_iter(G, num_paths, path_length, alpha=0,rand=random.Random(0)):# 流式处理用walks =nodes = list(G.nodes())for cnt in range(num_paths):rand.shuffle(nodes)for node in nodes:yield G.random_walk(path_length, rand=rand, alpha=alpha, start=node)def clique(size):return from_adjlist(permutations(range(1,size+1)))# http://stackoverflow.com/questions/312443/how-do-you-split-a-list-into-evenly-sized-chunks-in-pythondef grouper(n, iterable, padvalue=None):"grouper(3, 'abcdefg', 'x') --> ('a','b','c'), ('d','e','f'), ('g','x','x')"return zip_longest(*[iter(iterable)]*n, fillvalue=padvalue)def parse_adjacencylist(f):adjlist = []for l in f:if l and l[0] != "#":introw = [int(x) for x in l.strip().split()]row = [introw[0]]row.extend(set(sorted(introw[1:])))adjlist.extend([row])return adjlistdef parse_adjacencylist_unchecked(f):adjlist = []for l in f:if l and l[0] != "#":adjlist.extend([[int(x) for x in l.strip().split()]])return adjlistdef load_adjacencylist(file_, undirected=False, chunksize=10000, unchecked=True):if unchecked:parse_func = parse_adjacencylist_uncheckedconvert_func = from_adjlist_uncheckedelse:parse_func = parse_adjacencylistconvert_func = from_adjlistadjlist = []t0 = time()total = 0with open(file_) as f:for idx, adj_chunk in enumerate(map(parse_func, grouper(int(chunksize), f))):adjlist.extend(adj_chunk)total += len(adj_chunk)t1 = time()logger.info('Parsed {} edges with {} chunks in {}s'.format(total, idx, t1-t0))t0 = time()G = convert_func(adjlist)t1 = time()logger.info('Converted edges to graph in {}s'.format(t1-t0))if undirected:t0 = time()G = G.make_undirected()t1 = time()logger.info('Made graph undirected in {}s'.format(t1-t0))return Gdef load_edgelist(file_, undirected=True):G = Graph()with open(file_) as f:for l in f:x, y = l.strip().split()[:2]x = int(x)y = int(y)G[x].append(y)if undirected:G[y].append(x)G.make_consistent()return Gdef load_matfile(file_, variable_name="network", undirected=True):mat_varables = loadmat(file_)mat_matrix = mat_varables[variable_name]return from_numpy(mat_matrix, undirected)def from_networkx(G_input, undirected=True):G = Graph()for idx, x in enumerate(G_input.nodes()):for y in iterkeys(G_input[x]):G[x].append(y)if undirected:G.make_undirected()return Gdef from_numpy(x, undirected=True):G = Graph()if issparse(x):cx = x.tocoo()for i,j,v in zip(cx.row, cx.col, cx.data):G[i].append(j)else:raise Exception("Dense matrices not yet supported.")if undirected:G.make_undirected()G.make_consistent()return Gdef from_adjlist(adjlist):G = Graph()for row in adjlist:node = row[0]neighbors = row[1:]G[node] = list(sorted(set(neighbors)))return Gdef from_adjlist_unchecked(adjlist):G = Graph()for row in adjlist:node = row[0]neighbors = row[1:]G[node] = neighborsreturn G
至于skipgram,大家可以直接用gensim工具即可.
from gensim.models import Word2Vecfrom gensim.models.word2vec import Vocablogger = logging.getLogger("deepwalk")class Skipgram(Word2Vec):"""A subclass to allow more customization of the Word2Vec internals."""def __init__(self, vocabulary_counts=None, **kwargs):self.vocabulary_counts = Nonekwargs["min_count"] = kwargs.get("min_count", 0)kwargs["workers"] = kwargs.get("workers", cpu_count())kwargs["size"] = kwargs.get("size", 128)kwargs["sentences"] = kwargs.get("sentences", None)kwargs["window"] = kwargs.get("window", 10)kwargs["sg"] = 1kwargs["hs"] = 1if vocabulary_counts != None:self.vocabulary_counts = vocabulary_countssuper(Skipgram, self).__init__(**kwargs)

应用

在推荐场景中,无论是推荐商品还是广告,用户和item其实都可以通过点击/转化/购买等行为构建二部图,在此二部图中进行随机游走,学习每个节点的向量,在特定场景,缺乏特征和标签的情况下,可以通过user2user或者item2iterm的方式,很好的泛化到其他的标签.GNN提取的向量也可以用于下游双塔召回模型或者排序模型.如果有社交网络,通过挖掘人与人直接的关系提取特征,供下游任务也是个不错的选择.当然大家也可以尝试在一些推荐比赛中用于丰富特征.
往期精彩回顾 本站qq群851320808,加入微信群请扫码:
