动态规划算法介绍

动态规划是算法题常见的算法之一，本文后续会基于动态规划算法介绍一系列的LeetCode算法题。在本文中，着重介绍动态规划算法的基本概念以及解题思路，并通过一系列的算法题来介绍动态规划算法。

1. 动态规划概述

在动态规划类型的算法题中，一般要求都是计算最值问题，例如连续子数组的最大和、礼物最大价值等。在这类型的题目中，本质上是就是穷举所有的可能项，然后找到最值。

但是，在这些题型中，往往通过穷举的方式求解是超出时间限制的，而动态规划对应的穷举是存在重复子问题的，而且，动态规划一定具备最优子结构，这样才可以通过子问题找到问题的最优解。但是如何通过子问题找到原问题的最优解就涉及到状态转移方程。

在这三个要素当中，最难的是写出状态转移方程。这也是动态规划算法最困难的地方。在此，本文提供一个思路：

• 找到对应的状态

• 明确dp数组的含义

• 找到dp数组的转换规则

• 边界条件的确定

2. 斐波那契数列

题目

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

递归

这种解题方式不需要多做介绍。直接上代码

func fib(n int) int {
if n<=1{
return n
}
return fib(n-1)+fib(n-2)
}

在递归类型的题型中，为了方便理解，最好画出递归树来深入理解递归类型题目的解法。

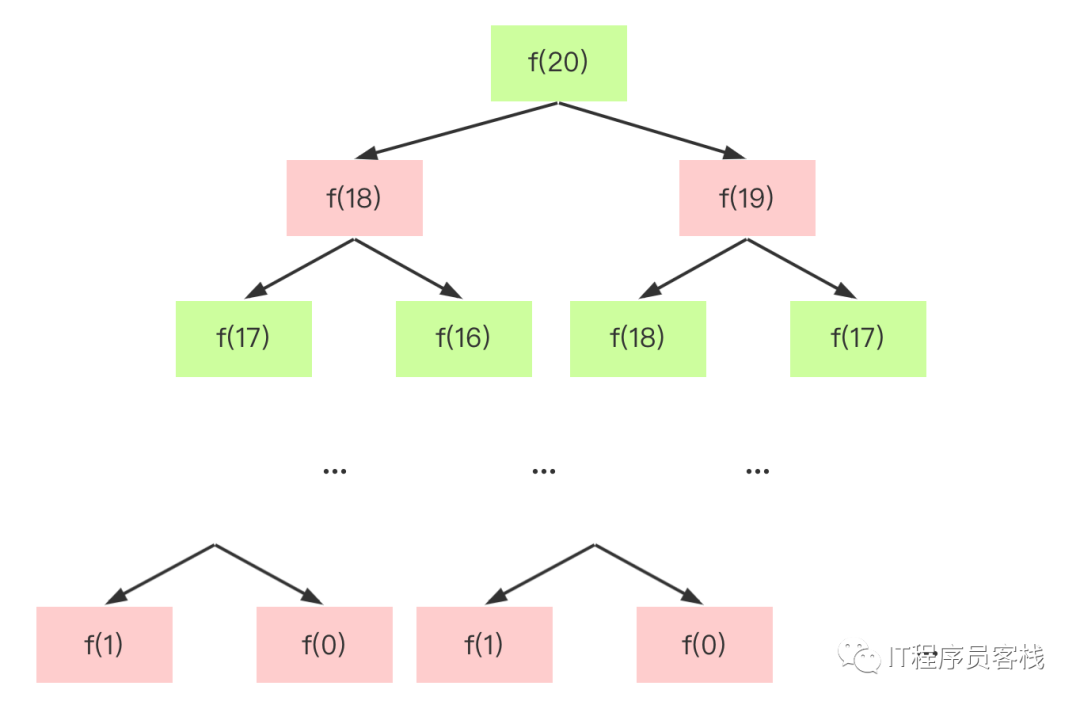
递归算法复杂度计算：子问题个数乘以子问题复杂度。在本题中，一共有n层，因此子问题个数为2^n，每个子问题解决需要的时间为O(1)，因此时间复杂度为O(2^n)。观察递归树，发现存在很多子问题重复的情况，例如计算dp[3]的时候需要重复计算dp[2],dp[1]。这就是动态规划第一个特性重复子问题

动态规划：自顶向下，备忘录求解

func fib(n int) int {
if n<=1{
return n
}
var memo =make([]int,n+1)
return help(memo,n)
}

func help(memo []int,n int) int{
if n<=1{
return n
}
// 如果不为0，则证明已经计算了
if memo[n]!=0{
return memo[n]
}
    memo[n]=help(memo,n-1)+help(memo,n-2)
return memo[n]
}

备忘录方式主要是保存子问题的解，在每次计算时优先从备忘录里面求解，这样就不需要每次都计算了，则通过备忘录优化，递归树转化为下述结构：

动态规划：自下向上

func fib(n int) int {
if n<=1{
return n
}
var dp=make([]int,n+1)
    dp[0]=0
    dp[1]=1
for i:=2;i<=n;i++{
        dp[i]=dp[i-1]+dp[i-2]
}
return dp[n]
}

这里介绍一下转移方程：

f(n)=f(n-1)+f(n-2) n>2
f(n)=n 0<=n<2

在本题中，发现dp[i]其实只和dp[i-1],dp[i-2]相关，则可以进行优化，将空间复杂度降低为O(1)

func fib(n int) int {
if n<=1{
return n
}
var numA=0
var numB=1
for i:=2;i<=n;i++{
        numB,numA=numA+numB,numB
}
return numB
}

其时间复杂度为0(n)，只有一个for循环语句。