追根溯源,算法岗面试「完整脉络」梳理:手推公式、通用问题、常见算法

极市导读
正值2021秋招季,本文梳理了常见的机器学习面试题的完整脉络,包括手推公式、机器学习通用问题以及常见机器学习、深度学习算法等。内容非常详尽,可为正在准备面试的同学提供有效参考。
一.常见手推公式部分
1.1 LR手推、求导、梯度更新

1.2 SVM原形式、对偶形式

1.3 FM公式推导
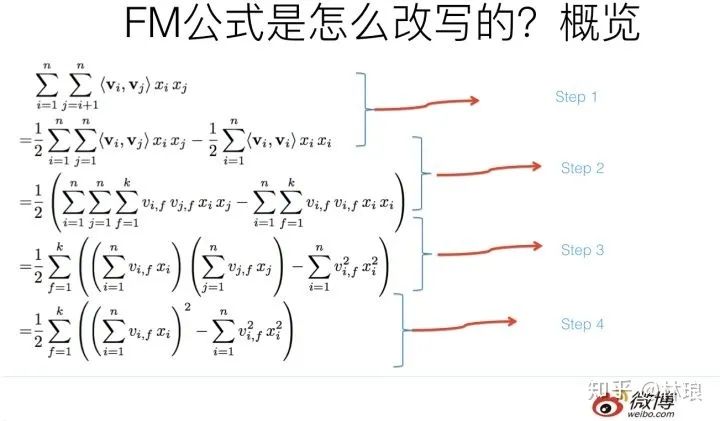
1.4 GBDT手推

1.5 XGB推导

1.6 AUC计算
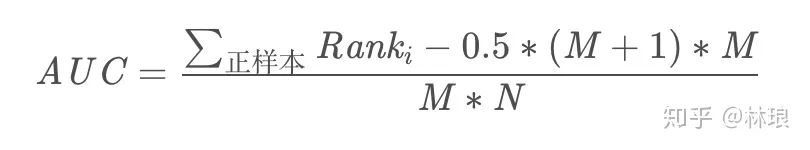

1.7 神经网络的反向传播

pytorch写简单DNN

二.常见机器学习通用问题
2.1评价指标
2.1.1 分类问题指标:
分类问题的评价指标大多基于混淆矩阵计算所得
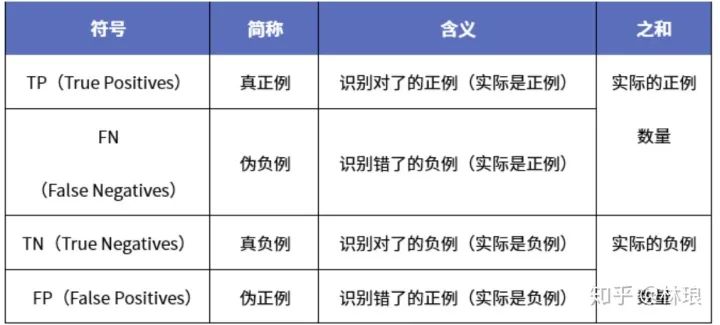
缺点:类别比例不均衡时影响评价效果。



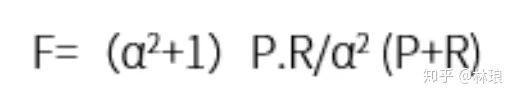
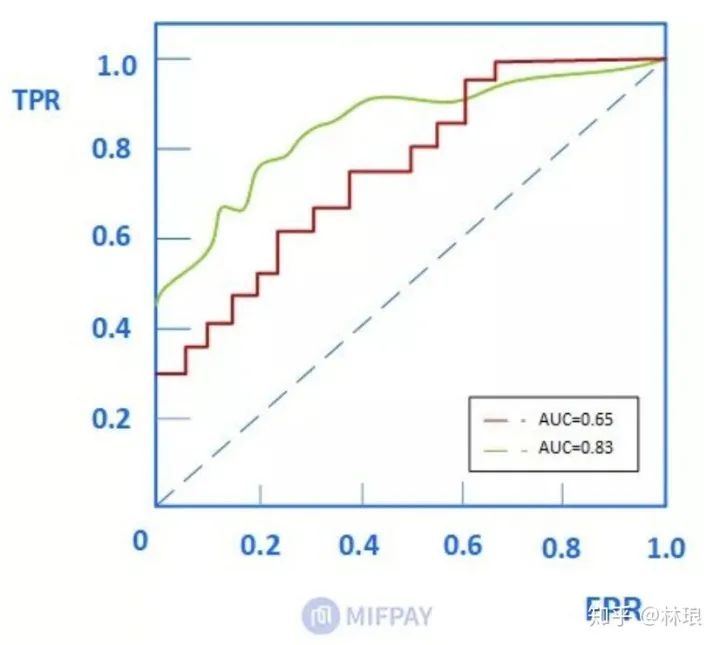
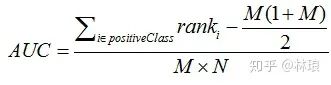
特点:AUC的评价效果不受正负样本比例的影响。因为改变正负样本比例,横纵坐标大小同时变化。整体不变。
2.1.2回归问题评价指标:
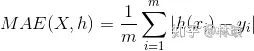
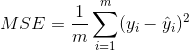
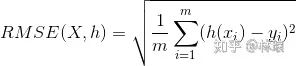
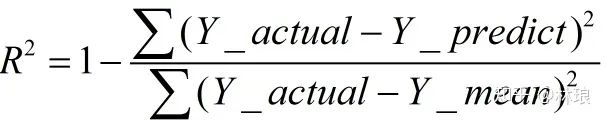
2.2.1 梯度下降法(gradient descent)
选择最陡峭的地方下山——这是梯度下降法的核心思想:它通过每次在当前梯度方向(最陡峭的方向)向前“迈”一步,来逐渐逼近函数的最小值。
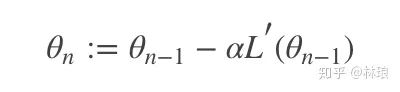

梯度下降法根据每次求解损失函数LL带入的样本数,可以分为:全量梯度下降(计算所有样本的损失),批量梯度下降(每次计算一个batch样本的损失)和随机梯度下降(每次随机选取一个样本计算损失)。
缺点:
2.2.2 Momentum
为了解决随体梯度下降上下波动,收敛速度慢的问题,提出了Momentum优化算法,这个是基于SGD的,简单理解,就是为了防止波动,取前几次波动的平均值当做这次的W。
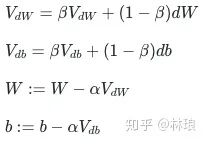
beta为新引入的超参,代表之前的dW的权重。

缺点:
依旧使用同一学习率alpha,比较难学习一个较好的学习率。
2.2.3 Adagrad
在前面介绍的算法中,每个模型参数θi使用相同的学习速率η,而Adagrad在每一个更新步骤中对于每一个模型参数θi使用不同的学习速率ηi。其更新方程为:
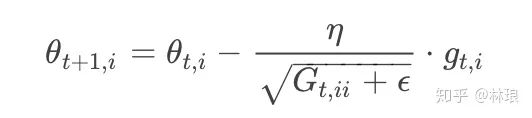
其中,Gt∈Rd×d是一个对角矩阵,其中第i行的对角元素eii为过去到当前第i个参数θi的梯度的平方和,epsilon是一个平滑参数,为了使得分母不为0。
缺点:
梯度衰减问题,Gt是不断增加的,导致学习率不断衰减,最终变得非常小。
2.2.4 RMSprop
RMSprop使用指数加权平均来代替历史梯度的平方和:
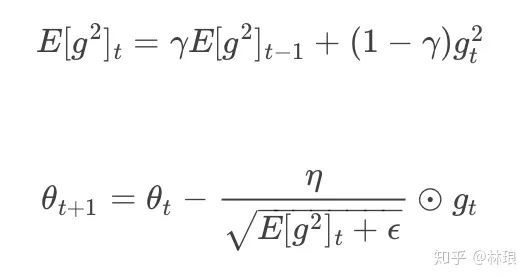
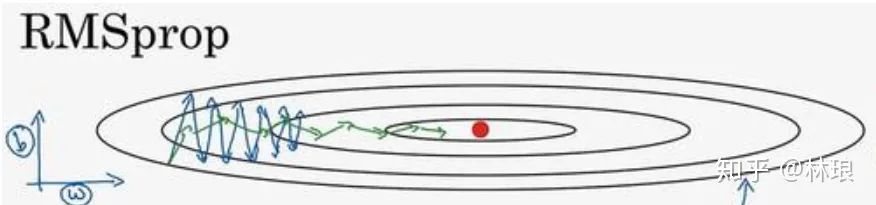
RMSprop对梯度较大的方向减小其学习速率,相反的,在梯度较小的方向上增加其学习速率。
缺点:
仍然需要全局学习率:n
2.2.5 Adam
Adam是Momentum 和 RMSprop的结合,被证明能有效适用于不同神经网络,适用于广泛的结构。是目前最常用的优化方法,优势明显。
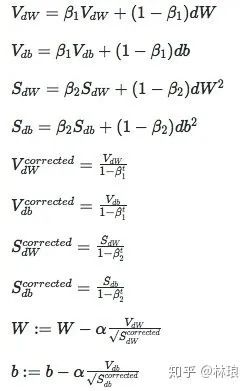
简单选择方法:
数据量小可以用SGD。
稀疏数据则选择自适应学习率的算法;而且,只需设定初始学习率而不用再调整即很可能实现最好效果。
Adagrad, Adadelta, RMSprop, Adam可以视为一类算法。RMSprop 与 Adadelta本质相同,都是为了解决Adagrad的学习率消失问题。
目前来看,无脑用 Adam 似乎已经是最佳选择。
2.3 过拟合问题
1.解空间形状:加入正则化项即为约束条件:形成不同形状的约束解空间。
2 导数:L2的导数为2X,平滑。L1导数为X,-X,存在突变的极值点
3.先验:加入正则化项相当于引入参数的先验知识:L1引入拉普拉斯,L2引入高斯分布
L1可以做到特征筛选和得到稀疏解。L2加速训练
减小参数规模
随机丢弃产生不同网络,形成集成,解决过拟合,加速训练
加快训练、消除梯度消失(爆炸)、防止过拟合 不适用太小batch、CNN
常见激活函数
sigmoid只做值非线性变化映射到(0,1),用于二分类。
softMax变化过程计算所有结果的权重,使得多值输出的概率和为1。用于多分类。指数运算速度慢。梯度饱和消失。
双曲正切函数。以0为中心,有归一化的作用。
大于0为1,小于0为0,计算速度快。
leaky输入为负时,梯度仍有值,避免死掉。
样本不平衡
模型评估指标
距离衡量与相似度
损失函数
MAE、MSE、Huber loss
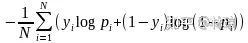
通过极大似然估计生成似然函数,取对数求极大值--损失函数
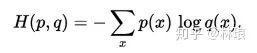
用一个猜测的分布的编码去编码真实的分布,得到的信息量
交叉熵p(x)对应真实标记y,q(x)对应预测值。
特征选择的方法
覆盖率、皮尔逊相关系数、Fisher、最大方差阈值、卡方检验
决策树剪枝
WOE/IV值计算公式
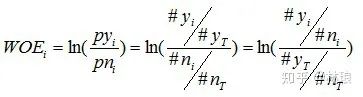
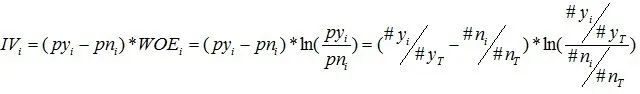
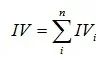
常见的数据分箱方法
处理海量数据方法
Kmean缺陷与改进
随机森林
criterion:度量分裂质量,信息熵或者基尼指数
max_features:特征数达到多大时进行分割
max_depth:树的最大深度
min_samples_split:分割内部节点所需的最少样本数量
bootstrap:是否采用有放回式的抽样方式
min_impurity_split:树增长停止的阀值
XGB

max_depth、min_child_weigh:树深,孩子节点最小样本权重和
gamma、alpha、lambda:后剪枝比例,L1,L2正则化系数
subsample、colsample_bytree:样本采样、列采样
eta:削减已学树的影响,为后面学习腾空间
tree_method:gpu_histGPU 加速
LGB
-常用调参:
num_iterations、learning_rate:迭代次数,学习率
max_depth、min_data_in_leaf、num_leaves:控制树的大小
lambda_l1、lambda_l2、min_split_gain:L1、L2、最小切分
feature_fraction、bagging_fraction:随机采样特征和数据
device:GPU
GBDT、XGB、LGB比较
1.损失函数:加入正则化项:L1叶子节点数,L2叶子节点输出Score
2.导数:使用代价函数的二阶展开式来近似表达残差
3.基分类器:XGB支持线性分类器做基分类器
4.处理缺失值:寻找分割点时不考虑缺失值。分别计算缺失值在左右的增益。测试首出现缺失,默认在右。
5.近似直方图算法:采用加权分位数法来搜索近似最优分裂点 6.Shrinkage(缩减):将学习到的模型*系数,削减已学模型的权重
7.列采样:特征采样。
8.并行计算:特征预排序,特征分裂增益计算(均在特征粒度上)
1.节点分裂准则:XGB一次分裂一层节点(浪费),LGB深度优先分裂(过拟合)
2.决策树算法:基于histogram直方图分箱操作。减存加速
3.直接支持类别特征,无需独热操作
4.特征并行,数据并行
5.GOSS:单边采样:保留大梯度样本,随机采样小梯度样本
6EFB:归并很少出现的特征为同一类
Stacking和Blending
LDA、PCA与SVD
线性判别分析 Linear Discriminate Analysis(监督)
PCA用于方阵矩阵分解
SVD用于一般矩阵分解 - LDA(类别区分最大化方向投影)
在标签监督下,进行类似PCA的主成分分析
构造类间的散布矩阵 SB 以及 类内散布矩阵 SW - PCA(方差最大化方向投影) 构建协方差矩阵 最大化投影方差:信号具有较大方差,让数据在主轴方向投影方差最大 最小平方误差:方差最大,即样本点到直线距离最小(最小平方误差)
- SVD
左右为正交矩阵:用于压缩行、列 中间为对角阵:奇异值
SVM
方便核函数的引入(转化后为支持向量内积计算,核函数可以在低纬中计算高维的内积),改变复杂度(求W变成求a(支持向量数量))
有效性:核函数矩阵KK是对称半正定矩阵
常见核函数:线性核函数,多项式核函数,高斯核函数,指数核函数
区别:线性简单,可解释性强,只用于线性可分问题。多项式可解决非线性,参数太多。高斯只需要一个参数,计算慢,容易过拟合。
特征维数高选择线性核
样本数量可观、特征少选择高斯核(非线性核)
样本数量非常多选择线性核(避免造成庞大的计算量)
EM
用于含有隐变量的概率模型参数的极大似然估计
推荐阅读

