6节上海交大暑期学校硬核深度学习理论课(附PPT下载)

导读:这个在线暑期学校旨在介绍近几年深度学习理论的进展,包括均值场理论、神经切核、函数空间理论、隐式正则化、频率原理等。不同观点之间的相互作用可能会对深度学习理论的发展有所启示。
来源:上海交通大学自然科学研究院、专知(ID:Quan_Zhuanzhi)

在线暑期学校主页:
https://ins.sjtu.edu.cn/schools/2020/07/16/online-summer-school-of-deep-learning-theory/1775
公众号后台对话框回复暑期学校,查看&下载以上PPT完整版。
01 均值场神经网络
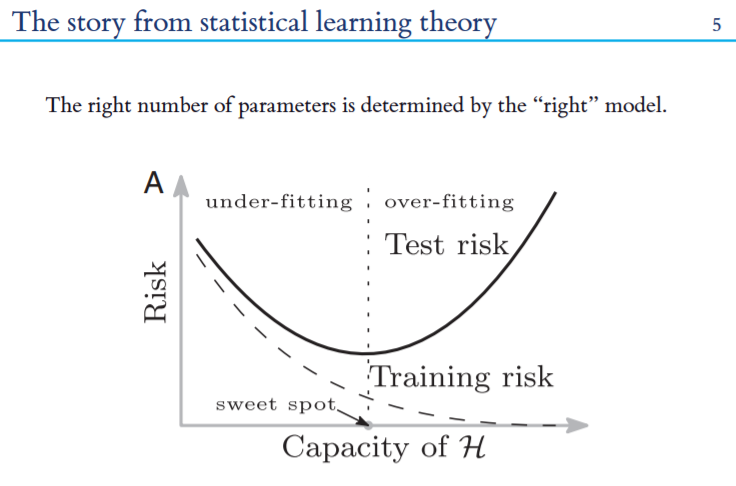
神经网络的精确性和可训练性:近似和优化的均值场视角
最近,对于深度神经网络理论研究有了一定突破。其中一支就是平均场理论(mean-field theory)。通过理论角度研究网络的初始化,研究者发现了两个影响网络训练的因素,一个是前向传播时网络对于不同样本的表达性(expressivity)以及反向传播时梯度消失爆炸问题,我们用可训练性(trainability)一词来描述关于梯度是否出现消失爆炸问题。
表达性以及可训练性这两个因素确定了深度网络能够成功训练的超参数范围。关于这一论断,研究者已经在全连接网络(fully connected network),卷积神经网络(CNN),递归神经网络(RNN),以及残差神经网络(Residual network)等等上面得到了实验验证。
在平均场理论基础上,研究者通过研究Input-output Jacobian矩阵的谱分布,发现网络初始化的另一个性质,dynamical isometry,即Jaconbian矩阵的奇异值分布集中在1附近时,网络的训练速度会特别快。利用这个结论,研究者成功训练了在没有batch normalization以及resnet结构帮助下的单纯一万层的卷积神经网络。


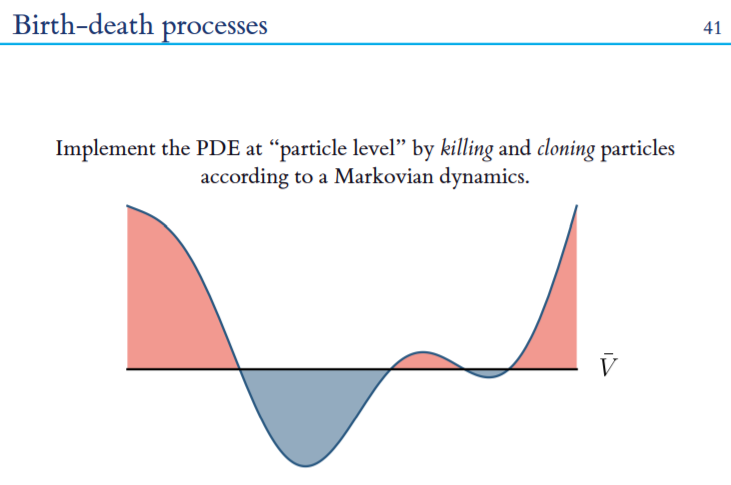
02 神经切内核-DNNs的收敛和推广
现代深度学习使得大型神经网络得到普遍使用,但研究这类网络的理论工具仍然缺乏。神经正切核(NTK)描述了输出神经元在训练期间是如何进化的。
在无限宽极限下(当隐藏神经元数增长到无穷大时),NTK收敛到一个确定的、固定的极限,导致对无限宽DNN的动力学的简单描述。NTK受网络架构的影响,因此有助于理解架构的选择如何影响DNNs的收敛和泛化。
随着网络深度的增长,出现了两种机制。冻结状态下,NTK几乎是恒定的,收敛速度缓慢;混沌状态下,NTK接近 Chaotic regime,这会加快训练速度,但可能会损害泛化。增加初始化偏差的方差将网络推向冻结状态,而层归一化和批归一化等归一化方法将网络推向混沌状态。
在GANs中,冻结状态导致模态崩溃,其中产生器收敛于一个常数,并导致棋盘图案,即图像中的重复图案。当产生器处于混沌状态时,这两个问题都得到了很好的解决,这说明了批量归一化在GANs训练中的重要性。




03 神经网络模型的函数空间理论和泛化误差估计



我们建立了神经网络模型的函数空间理论,定义了两层神经网络的Barron空间和残差网络的流诱导函数空间
直接定理和逆定理表明,函数空间包含所有的函数,可以被表现良好的神经网络(没有维数的诅咒)近似,规范控制常量因素。范数还可以控制估计误差。
通过RKHS、Barron空间和合成空间的比较,可以看出残差网络优于两层网络,两层网络优于核方法。
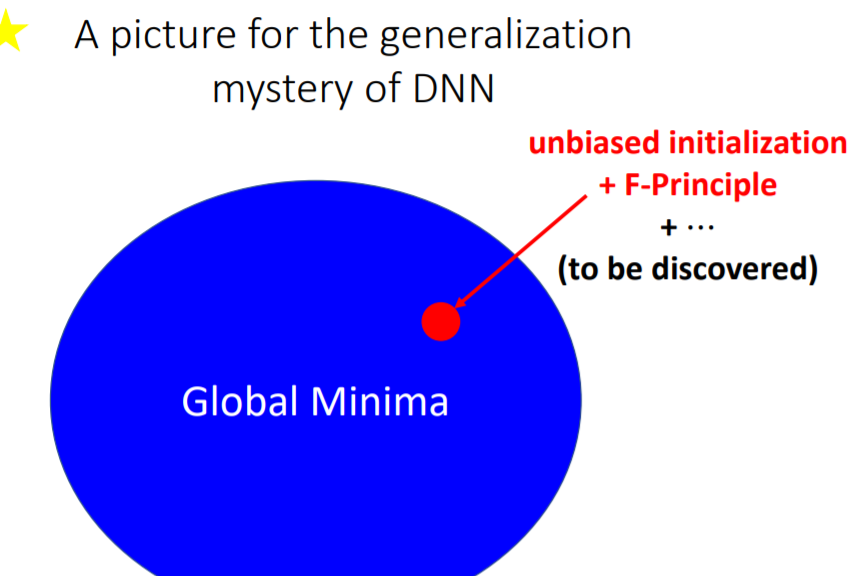
04 对深度学习中隐式正则化的理解
对于神经网络模型,GD或SGD总能很好地找到可泛化的解决方案。与隐式正则化相比,显式正则化,例如权值衰减、退出等,只能略微提高泛化性能。明确的正则化在某些场景中可能是非常重要的,例如高噪声数据、无监督学习(GAN)等。


05 频率原理:线性模型和一般理论


06 神经正切核



公众号后台对话框回复暑期学校,查看&下载以上PPT完整版。


