聪明人的贝叶斯陷阱：一胎是女孩，二胎生男孩的概率竟是？（烧脑强文）-技术圈

导读：打开这篇文章的，多半是聪明人。欢迎你掉入聪明人的陷阱。

作者：老喻在加

来源：孤独大脑（ID：lonelybrain）

世界的真正要素不是物，而是颜色、压力、空间、时间这些我们称之为感觉的东西。

因此，所谓的“科学知识”绝不是客观实在及其规律的反映，而只是对这些感觉要素的简单化、物化的处理方式而已。

——马赫

开始前，我想问你一个问题：

你相信意识可以移动物体吗？

“观察者效应”这个话题，经常以科学传说与心灵药方的形式，出现在对量子力学与人类精神层面（霍桑效应）的“叶公好龙”行为中。

根据量子理论，粒子在没有被观测时处于多种本征态的叠加状态，而当我们观测粒子的状态时，它就会塌缩到一个确定的本征态。

大白话说，就是观察者可以“超距”地改变被观察的对象。

观察者为什么会影响亚原子层面的“现实”，会涉及到人的意识、量子塌缩、大脑中可能存在量子计算过程等等概念，这些概念如今已经以科学的名义娱乐化、玄学化了。

今天我要写的，是“观察者效应”对经典力学的日常经验的作用，这看起来似乎有点儿怪。

在量子力学里，电子在某一时刻的状态，是由电子在所有固定点的状态按一定概率叠加而成的，或可称之为电子的量子“叠加态”。这就是所谓薛定谔的猫。
但是，在经典物理里，物体任何时候都会“确定地”处于空间中的某个点。

比如你可以说我的手机有一半可能在卫生间，也有一半可能掉在车上，这是一个概率预测。

可我们不能说：手机是由卫生间的状态和车上的状态叠加而成。

那么，“观察者效应”会将你丢失的手机从卫生间“移动”到车上吗？

我的回答是：能。

本文的话题即使是在专业领域的聪明人之间，也经常引发争议。

我们会从两个简单的问题开始，一步步深入到令聪明人着迷的神秘地带。

更有趣的是，在答题之后，我还将以可感知的方式，提及两个烧脑的概念：

信息之做功；
“主观观察”改变“客观世界”。

假如你对前面的解题很厌倦，可以直接跳到第八段的“哲学思考”：

我们与这个世界的关系，不是去探寻“世界是什么”，而是人类观察世界的方式。

让我们立即开始吧！

蒙洛迪诺曾经与霍金合著过《时间简史》，他的《醉汉的脚步》是一本非常棒的讲概率和随机性的书。

在讲到“样本空间”这个概念时，蒙洛迪诺出了一道题：

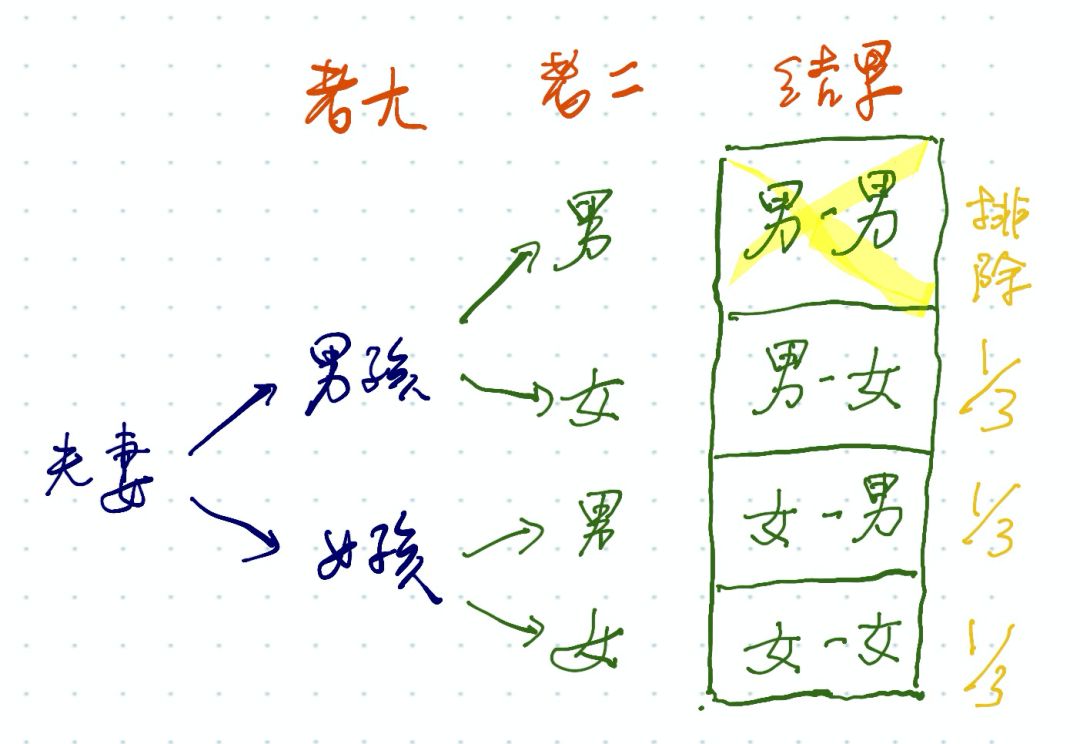
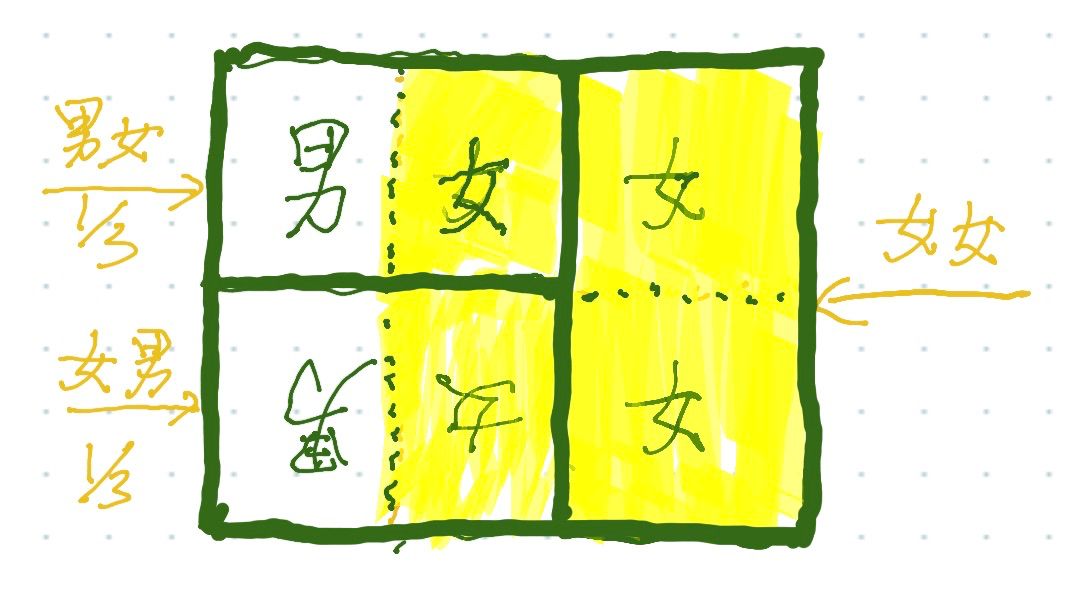
题目A：生男生女

一家两个小孩，已知生男生女概率相同，已知一个是女孩。

请问另外一个也是女孩的概率是多少？

这道题看起来似乎很简单：

已知一个是女孩，另外一个要么是男孩，要么是女孩，答案应该是1/2呀？

解答：根据样本空间的概念，也就是我在为什么真正聪明的人都是概率高手？（零公式入门篇）里说的“平行宇宙”，用穷举法，两个小孩有如下四种可能--

第一胎：男，男，女，女
第二胎：男，女，男，女

所以，已知有一个是女孩，所以排除第一种可能，剩下三种可能性，答案是1/3。示意图如下：

对于本题的让人迷惑之处，蒙洛迪诺解释道：如果我们指定了哪一个是女孩，例如老大是女孩，那么另外一个也是女孩的概率就变成了50%。

如上图：因为一旦指定了老大是女孩，上面的四种可能性中，要把“男-男”和“男-女”两个可能从样本空间中去掉，这样只剩下“女-男”和“女-女”，所以“女-女”的概率是50%。

然而，另外一个聪明人“不赞成”这个答案。

他就是加里·史密斯，耶鲁大学博士，曾在耶鲁大学任教7年，其间两度获得教学奖。

他在《简单统计学》一书中，指名道姓地批评了蒙洛迪诺的“谬误”。

加里·史密斯用另外一种方式陈述了题目：

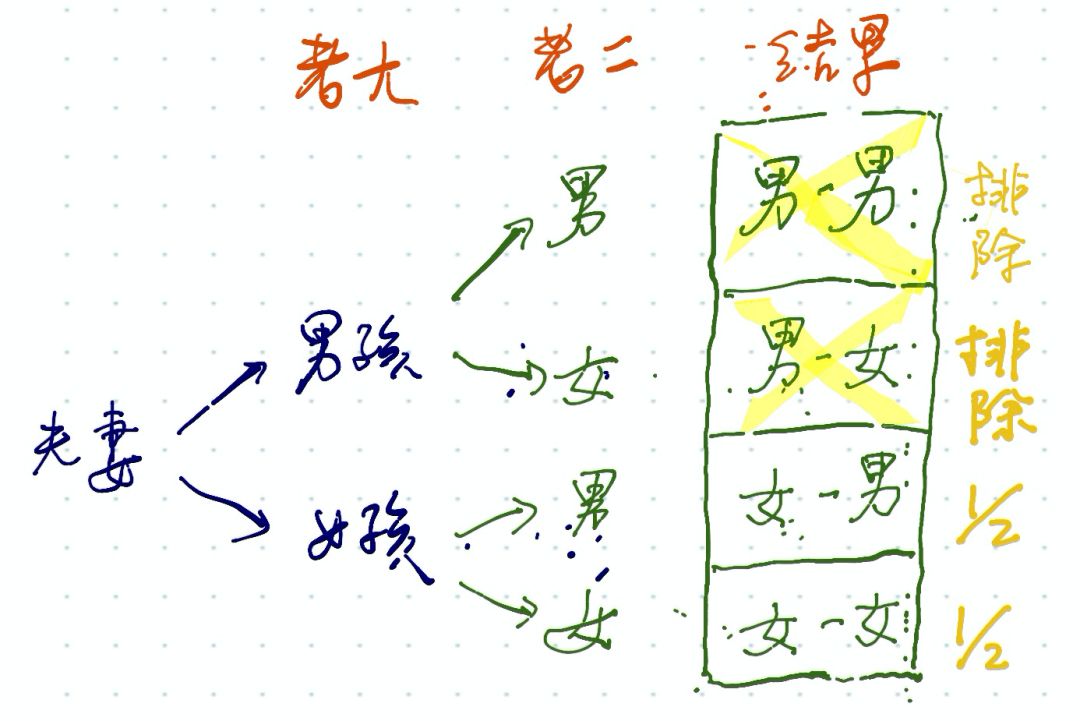
题目B：另一个孩子

一个名叫史密斯的男人正在和他的女儿散步。

史密斯说，他们家还有一个孩子。

请问：这个不在身边的孩子是女孩儿的概率是多少？

看起来这道题的表述似乎和蒙洛迪诺的题“类似”，然而加里·史密斯有完全不同的解答。

首先他毫不留情地批评“专家”们“三分之一”的答案错了。

加里·史密斯给出了一个表格：

B是指男孩，BB就是指老大男孩老二也是男孩。

G是指女孩，BG就是指老大男孩老二是女孩。

上图显示了在 BB、BG、GB 和 GG 之间均匀分配的 400 个家庭。

让我们不厌其烦地跟着作者分析一遍。

已知：

在史密斯有两个男孩儿的 100 种情况中（BB），他总是和一个男孩儿散步。
在史密斯有两个女孩儿的 100 种情况中（GG），他总是和一个女孩儿散步。
在他拥有一儿一女的情况中（BG 或 GB），一个合理的假设是，他与男孩儿或女孩儿散步的概率相等。

分析：

观察第一行，即史密斯和女孩儿散步的 200 种情况。在 100 种情况中（GG），不在场的孩子是女孩儿，在另外 100 种情况中（BG 或 GB），不在场的孩子是男孩儿。
在第二行里（史密斯和男孩儿散步的 200 种情况），在 100 种情况中（BB），不在场的孩子是男孩儿，在另外 100 种情况中（BG 或 GB），不在场的孩子是女孩儿。

结论：不管和史密斯散步的孩子是女孩儿还是男孩儿，他的另一个孩子是男孩儿或者女孩儿的概率都是相等的。

（以上图表和分析来自《简单统计学》，后面我会给个更简单更形象的计算。）

所以，答案应该是1/2，而不是1/3。

当然，这个问题也能够用常识直接回答掉：看到一个是女儿，和另外一个是男还是女没关系。

所以另外一个是女孩的概率是1/2。为什么要计算那么复杂呢？

原因在下面。

假如你没有感到一点点晕，那么你可能并不是真的懂。

那么霍金的合著者，与耶鲁大学的博士，到底谁对谁错呢？

真相是：

两个人的答案都是对的。
但“耶鲁博士”对“霍金合著者”的批评是错的。

那问题出在哪儿呢？

原因是：

这两位牛人讨论的题目，压根儿不是同一个。

我们再来看一下。

（霍金的合著者）题目A：

两个孩子，已知至少有一个是女孩，另外一个是女孩的概率是多大？

（耶鲁大学博士）题目B：

两个孩子，亲眼看见一个是女孩，另外一个是女孩的概率是多大？

难道这说的不是一回事儿吗？

“亲眼看见一个是女孩”，不就证明了“至少有一个是女孩”吗？

你觉得呢？

搞晕聪明人的时刻到了。

你看，即使是耶鲁的博士，也混淆了二者之间的区别。

（《简单统计学》是很好的书，而且也有较小概率是我说错了。）

最简单的方法是采用贝叶斯公式来计算，但是我继续采用零公式的方式，来做一些可感知的推理。

“至少有一个是女孩”，与“亲眼看见一个是女孩”，并非一回事情。

这个是关键。

这二者直接的差别，可以从空间、时间两个维度的“整体与局部关系”来揭示。

1. 先看空间维度的“整体与局部关系”

“至少有一个是女孩”，不能确保你亲眼看见的那个就是女孩。

尽管你可以由“亲眼看见一个是女孩”推理出“至少有一个是女孩”，但是，你不能由“至少有一个是女孩”推理出“亲眼看见一个是女孩”。

我用画图来形象描述一下：

如上图所示，“亲眼看见一个是女孩”被包含于“至少有一个是女孩”。也可以说，“亲眼看见一个是女孩”是比“至少有一个是女孩”信息更多的概率描述。

2. 再看时间维度的“整体与局部关系”

“至少有一个是女孩”，是上帝视角的统计结果；
“亲眼看见一个是女孩”，是人肉视角的观察结果。

我用时间维度来说，未必精确，但大致是一个形象化的描述。

如上图所描述——

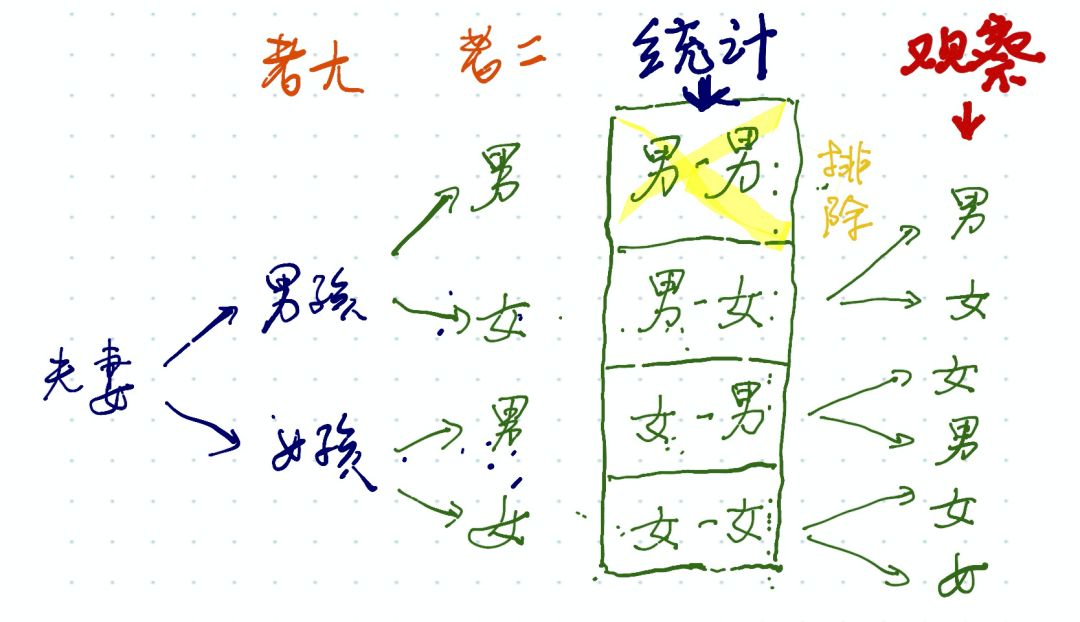
（蓝色字体）统计：上帝视角的统计结果，是对符合“至少有一个是女孩”的所有样本空间的整体描述；
根据上帝视角的统计，有三种样本空间，所以两个都是女孩的概率是1/3；
（红色字体）观察：人肉视角的观察结果，是对其中一个平行宇宙的实际结果“亲眼看见一个女孩”的真实描述。
根据人肉视角的观察，观察到是女孩的4类可能性，有一半来自两个都是女孩的样本空间，所以两个都是女孩的概率是1/2。

由此，我们终于引发了关键话题：

“亲眼看见一个是女孩”，是人肉视角的观察结果，也是一个做功的过程；
为什么一个（信息并不完备的）观察，会改变现实的可能性？

（埋一个彩蛋：假如上面的题目中，那个男人出门的时候就决定了要带一个女孩一起散步，那么，这个时候你正好看见了他和女孩，请问他有两个女孩的概率是多大？）

下面，我用另外一道好玩儿的题目，来测试一下“观察改变现实的可能性”。

题目：酒鬼去哪儿？

某酒鬼有90%的日子都会出去喝酒，喝酒只随机（概率均等）去固定的三家酒吧，也就是说去每家酒吧的概率都是30%。

今天警察想去抓酒鬼，结果找了其中两家酒吧，都没有抓到。

请问：酒鬼在第三家酒吧的该率？

答案是：

假如警察真的是想抓酒鬼，那么酒鬼在第三家酒吧的概率是75%；
假如警察是酒鬼的兄弟，不那么想抓他，酒鬼在第三家酒吧的概率是90%。（这个结果有一些不严格的假设。）

酒鬼这道题，最让人疑惑的地方是：

为什么警察“真的抓”和“假装抓”会影响酒鬼在第三家酒吧的概率？

也就是说，酒鬼在第三个酒吧是一个物理事件，而且在警察来抓之前就已经客观存在了，为什么会因为警察心底的主观意识而发生改变呢？

难道有心灵感应这回事儿吗？

请允许我用小白话来把题目分析一遍：

酒鬼去每个酒吧的概率都是30%，这是一个统计结果，也就是说过去100天，酒鬼有30天去酒吧A，30天去酒吧B，30天去酒吧C，10天回家被老婆骂。

那么具体到今天，他要么在三个酒吧中的某一个，要么在家里。不管他在哪儿，他都是百分之百在那里的。

既然如此，概率有什么用呢？是拿来分析可能性的。例如知道概率的大小，警察就知道去任何一家酒吧抓住酒鬼的可能性，都是在家里抓住他的可能性的3倍。一次未必准，但抓上很多次，就越来越接近这个比例。

图示如下：

让我们继续用零公式的方式，来计算一下这道题。

上图，是上帝视野的统计概率，而现在的情况是，警察去了酒吧A和酒吧B，发现酒鬼都不在。

这其实是一个观察过程。如下图：

经由观察，酒鬼在酒吧A和酒吧B的可能性消失了，相当于对应的平行宇宙“坍缩”了。

接下来，去酒吧C的30%和回家哭的10%，对应了全部可能性。

于是，如上图右侧的计算，在酒吧C的概率是75%。

这就是警察真的想抓酒鬼（且不知道酒鬼在哪儿）的情况下，酒鬼在酒吧C的概率。

那么假如警察知道酒鬼的情况呢？

在重新写本文时，我发现自己过去的文章对这种状况表达有误。

我试着更精确地表述：

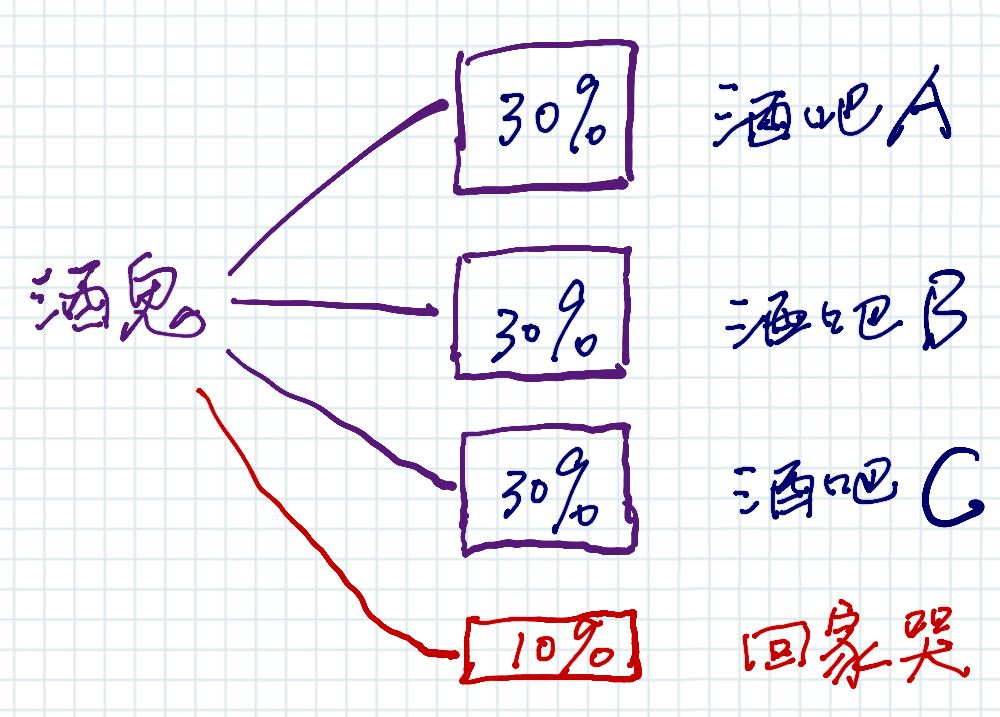
有两个警察一起去抓酒鬼。其中一个很正直，而另外一个坏警察与酒鬼有勾结。

酒鬼还是90%的概率去喝酒，10%的概率回家。

但是，为了不被抓，酒鬼和坏警察商量好，以后只去C酒吧喝酒。

当好警察打算抓酒鬼时，坏警察故意带好警察去A酒吧和B酒吧，以干扰抓酒鬼。

请问在C酒吧抓到酒鬼的概率是多少？

我发现，一旦想要精确地表述问题，问题就毫无趣味了：当然是90%了。

那么，我想继续追问：对于好警察来说，所做的事情还是一样，为什么在酒吧C抓到酒鬼的概率就从75%变成90%了？

（对比而言，“三门问题”更容易表达信息的做功，我将其放在后面了。）

对于好警察来说，他的旧情报还是酒鬼以各30%的概率分别去三个酒吧喝酒。

但是坏警察知道，酒鬼90%的概率是去C酒吧喝酒。

坏警察故意先带好警察去A酒吧和B酒吧，其实是利用自己基于更多信息的“概率权”。

在这种操纵下，好警察去A酒吧和B酒吧的观察行为，并不会导致对应的平行宇宙的“坍缩”。

抓酒鬼这个案例告诉我们：

判断是可以测度的，相关性的判断就是概率。

但是，问题往往出现在“相关性的判断”上。

同样，酒鬼被抓的可能性，似乎被知情且想包庇他的坏警察控制了。

这也是概率权。

相当多的概率争议，来自对表述的理解。

有些人认为是文字游戏。

然而，假如一个游戏导致长期的争议，那么一定不止是个文字游戏。

还是《简单统计学》一书，讲述了下面这个经典题目：

2010年，在两年一度纪念马丁·加德纳的“加德纳集会”上，加里·福希提出了这个问题的另一个版本。他走上讲台，说道：“我有两个孩子。一个是男孩儿，出生在星期二。我有两个男孩儿的概率是多少？”

停了一会儿，福希继续说道：“你能想到的第一件事情是，‘这和星期二有什么关系？’实际上，二者之间存在密切的关系。”

然后，福希走下了讲台。他的发言在会场和互联网上引发了一场热烈的讨论。

假如你去搜索一下，很容易找到这个“星期二男孩”的计算过程，以及答案：

13/27。

这是个很奇怪的数字，哪里来的13，又从哪儿来的27？

《简单统计学》的作者，耶鲁大学博士，对此毫不客气地说：

这和星期二的确没有任何关系。

他的推理如下：

如果星期二能够改变这个概率，那么星期三、星期四或者一周里的其他任何一天也能以同样的方式改变这个概率。
不过，这个孩子一定会出生在一周里的某一天。
因此，如果福希的说法是正确的，我们可以在不知道这一天是星期几的情况下改变这个概率。

他由此得出结论：福希是错误的。这一天是星期几并不重要。

到底谁是对的？

我们先看一下，13/27是怎么得来的。

对应该计算，我将该问题表述得更加精确一些：

某人有两个孩子。一个是男孩儿，出生在星期二。他来自有两个男孩儿的家庭的概率是多少？

我继续用“平行宇宙法”，也就是可视化的穷尽法，来计算一下结果。

如下图：

我列举了符合“有一个星期二出生的男孩”的所有可能性。

请注意，这里仍然是上帝视角的统计分布，认为这是用贝叶斯公式来计算的理解是错误的。

上图右侧的三个7✖️7表格，横坐标是老大从周一到周日的可能性，纵坐标是老二从周一到周日的可能性，对应的一共是49种可能性。

但是因为符合“星期二男孩”的，只有表格中标为红色的可能性：

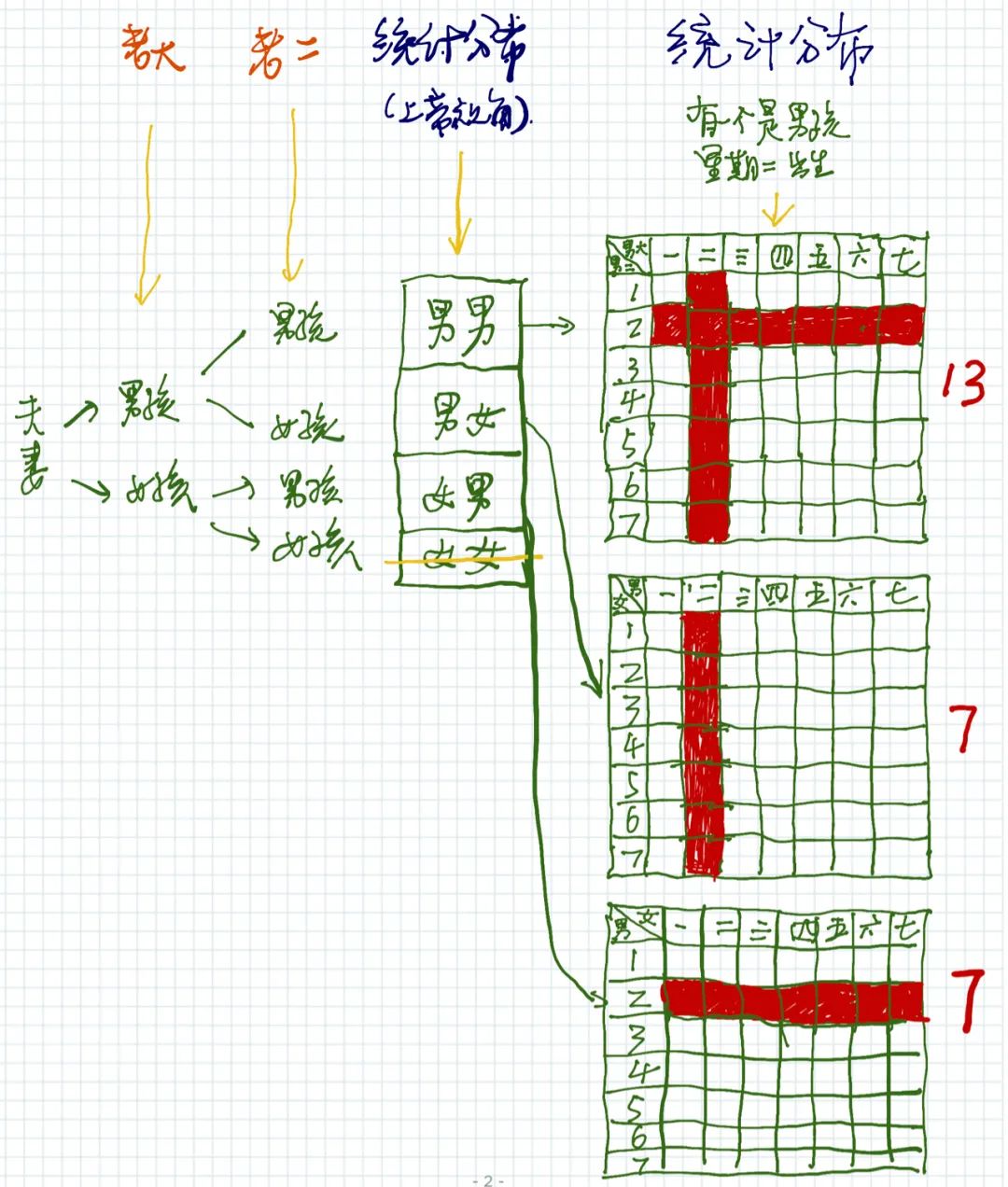
在“男男”组合里，符合条件的有13种；
在“男女”组合里，符合条件的有7种；
在“女男”组合里，符合条件的有7种。

以上合计27种符合“有一个星期二出生的男孩”的可能性。

其中，有13种是“男男”组合，所以该组合的概率是13/27。

为什么看起来如此“简单”的计算，会引发如此大的争议？

上面的耶鲁博士错了吗？

即使算出了13/27的人，对这个问题的理解也大多错误了，他们混淆了条件概率，也没搞对贝叶斯公式的本义。

然而，我打算继续发挥自己外行的优势，跳出使用“概念”的歧义，来深挖争议的本质。

我将改造一下上面的题目：

假如某人有两个孩子，有一天我给他家打电话，是他其中一个孩子接的，是个男孩，我问他是周几出生的，他说是星期二。

请问，他有两个男孩的概率是多大？

请注意，这时，“有个星期二男孩接电话”，就变成了一次“观察”。

如前所述，这次主观参与的观察，改变了概率。

发生过程如下：

如上图，第四列“统计”，是计算出13/27的过程。

第五列“观察”，从上帝视角，变成了观察者视角。

其中最大的变化是：

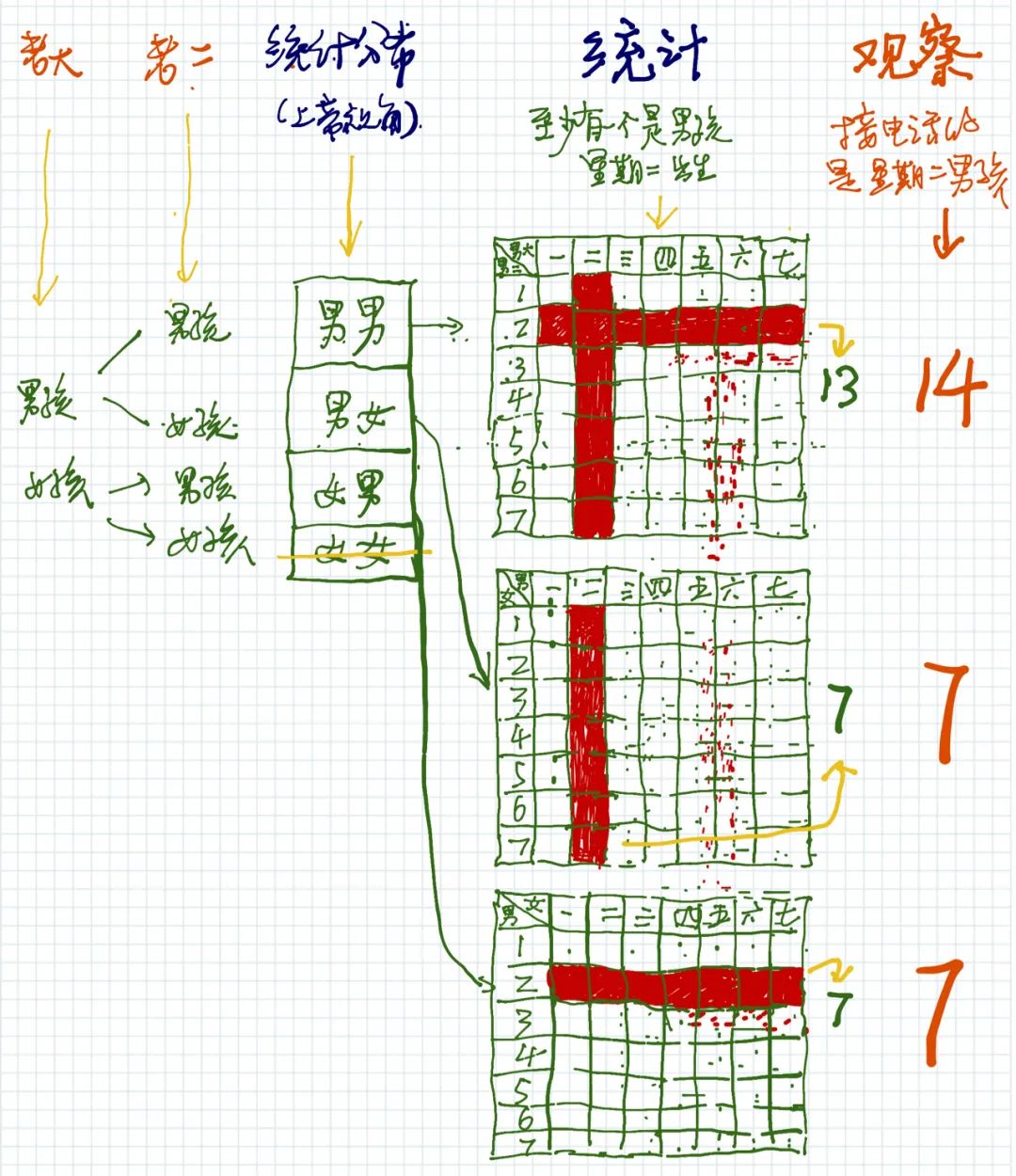
在“男男组合“的49种空间组合里，也就是在第四列“统计”中，是13种。
在第五列“观察”里，对应“男男组合“的13种空间可能性中，有14个星期二男孩可能会被观察到接电话。

图示如下：

请注意上图，变化（也就是歧义发生的地方），位于两条红带的交叉点：

两个男孩都是星期二男孩。

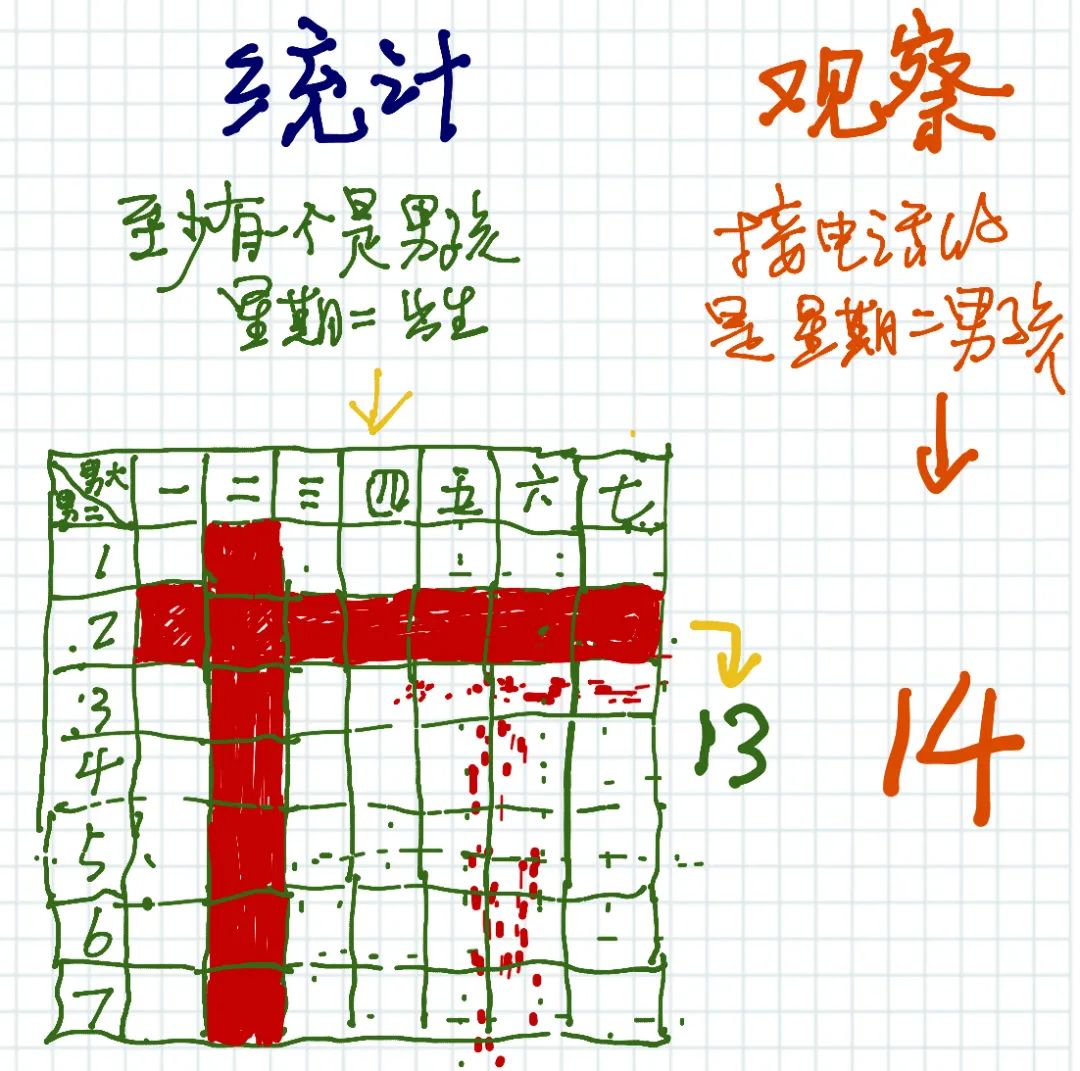
作为上帝视角的统计，即使有两个星期二男孩，作为样本空间，其可能数量还是1；
但是从观察者的角度，针对交叉点的“两个都是星期二男孩”的样本空间，观察到的可能是老大，也可能是老二，所以在该点符合条件的观察结果是2。

从观察者的结果计算逆概率，用的才是贝叶斯公式：

被观察到的星期二男孩，家里有两个男孩的概率是“14/28”，也就是1/2。

写《简单统计学》的耶鲁博士，说的是上面这种状况。

13/27，和14/28，两个结果都没错：

前者说的是上帝视角的样本空间可能性；
后者说的是观察者由果至因的概率计算。

观察结果，相当于获得了更多的信息，因此改变了概率。

前面“两孩问题”生出了1/3与1/2两种不同结果，道理和这个是一样的。

观察，看似只是主观的、外部的参与，但是从信息的角度，从概率的角度，相当于“做功”，会导致概率变化。

这里特别要提到的是，“接电话的是个男孩”，与“接电话的是个星期二男孩”，这两个貌似不同的观察结果，所得出的“两个孩子都是男孩”的概率都是1/2。

为什么呢？

因为对于观察者而言，“星期二”并没有给出更多信息。说男孩出生于星期二，相当于一句废话。

这大概也是香农对信息的定义。

让我们再回到文章的开头，看看那两道简单点儿的题。

（霍金的合著者）题目A：

两个孩子，已知至少有一个是女孩，另外一个是女孩的概率是多大？

这道题目，其实是关于“样本空间”的概率问题。

所以基于下图之“统计”那一列，可以得出结果是1/3。

（耶鲁大学博士）题目B：

两个孩子，亲眼看见一个是女孩，另外一个是女孩的概率是多大？

这道题目，其实是关于从“结果”推理“原因”的计算，对应的是下图“观察”那一列。

从“结果”推理“原因”，是一个贝叶斯计算。

我们不用公式，就可以清晰地推理计算。

看见一个女孩，只会发生在“男女、女男、女女”三个样本空间里。

所以，当“亲眼看见一个女孩”，问另外一个是女孩的概率是多大，其实是在问：

两个孩子，亲眼看见一个是女孩（果），那么她来自“女-女”家庭（因）的概率是多大？

我把“男女、女男、女女”三个样本空间重新摆成下面这个样子，因为面积代表可能性的数值（平行宇宙的胖瘦），这样就可以“可视化+可计算”了。

（上图三个长方形的面积是一样的。）

因为“亲眼看见一个是女孩”，这个观察结果，发生在上图黄色区域里。

根据面积比例可以发现，“女-女”占了观察结果是一个女孩的可能性的50%。

我们很容易得出结论：

根据“看见一个女孩”这个观察结果，她来自“女-女”家庭的可能性是50%。

所以，当你亲眼看见一个女孩，另外一个也是女孩的概率是50%。

这里有点儿“诡异”的地方是，“亲眼看见一个女孩”这个“果”，更新了我们对于这个女孩来自于什么家庭（因）的“信念”。

意识能够搬动物体吗？

假如一个人说他能用意识让勺子变弯，那么他要么是魔术师，要么是骗子。

意识控制机器是另外范畴的事情，让爱因斯坦疑惑的“魔鬼般的超距作用”也不是我的讨论目标。

我想说的是：

意识可以改变现实世界的概率吗？

我不得不再次提及“三门问题”，但是会写到一些你在别处可能没见过的思考。

已知：在下面三道门中，你选择了A。具体规则和过程请看下面。

说这道题太简单的人都是不诚恳的。当年在美国，这道题搞晕了一大堆大学教授、数学家、博士在内的专业人士和聪明人。

疑惑在于：

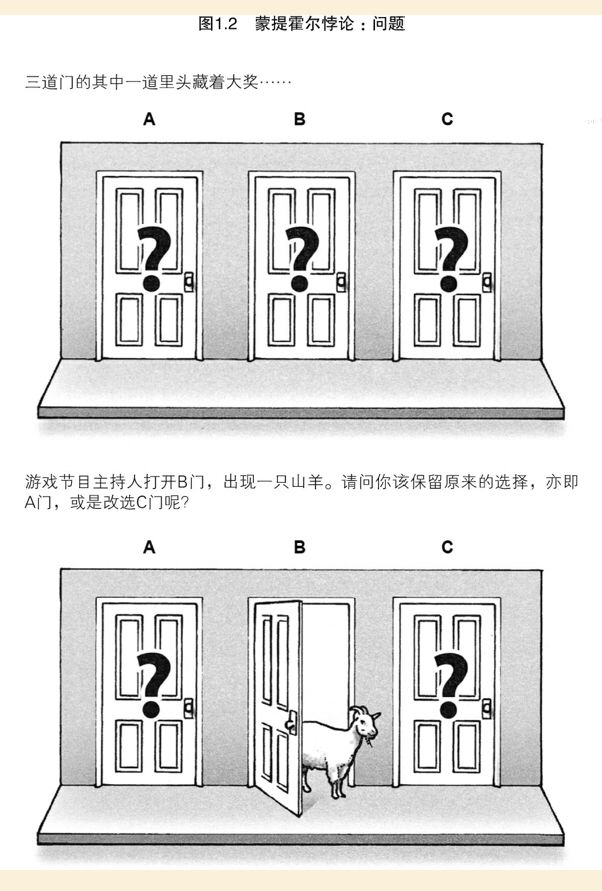
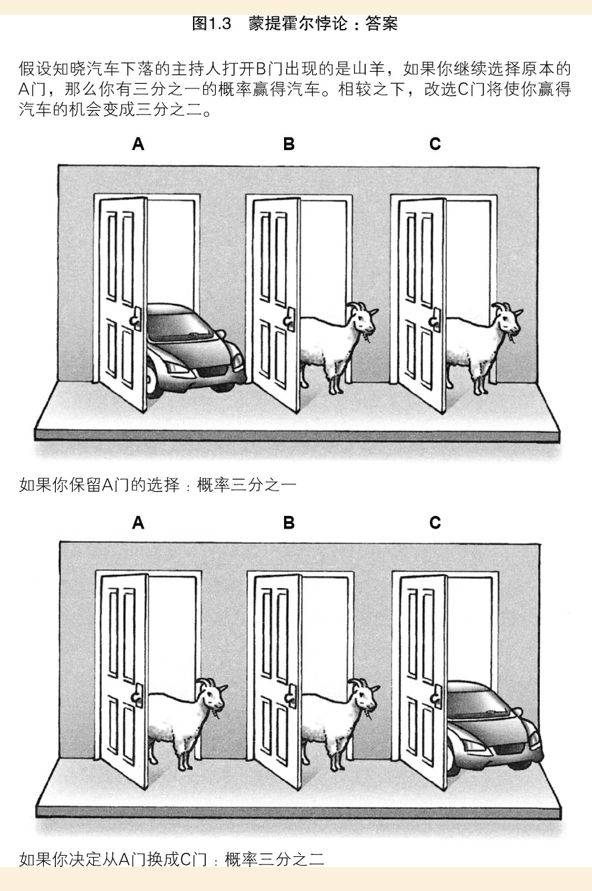
打开一扇门之后，剩下两扇门，难道每扇门之后有汽车的概率不是一样的50%吗？
如果主持人打开一扇门，那扇门原有的1/3可能性，为什么全部分配到C门了？A和C有什么区别呢？
到底是什么神秘的力量，导致了概率的重新分配？

即使你知道并理解了这个问题的答案，还是可能忽略了本题的一个关键点：

主持人到底是否知道B门的后面没有汽车。

《不确定世界的理性选择》对此有精确描述：

主持人的规则至少有三种可能的解释。

第一种规则：主持人总是随机打开没有被参与者选择的门（例如，在上面的情境中，主持人掷一枚硬币来决定打开 2号或 3号门）。这表示主持人可能打开一扇门并展示出门后的轿车，然后（和观众一起）笑话你选错了门，游戏结束。
第二种规则：假设主持人总是挑选后面藏着山羊的门打开，决不打开参与者挑选的门；当参与者已然选中了藏有轿车的门，主持人就随机打开一扇门。这样，参与者的选择和主持人开门之间的关系就更复杂了。
第三种规则：假设主持人总是挑选藏有山羊的门打开，决不打开参与者挑选的门；在参与者已然选中了藏有轿车的门之后，主持人有偏向地挑选剩下两扇门中序号较小的一扇打开（针对这种规则可能存在其他偏差）。

尽管这三种规则均符合上述问题的表述，但其潜在概率却各不相同。

在上面的题目里，我们留意到，主持人前面有个定语：

假如他知晓汽车的下落。

那么问题来了，假如主持人不知道汽车在哪个门的后面，这时他打开B门，发现后面没有汽车，那你换不换？

答案是：不换。或者说换不换无所谓。因为这时A和C后面有汽车的概率，都是1/2。

但是更聪明的思考应该是：

假如你不知道主持人到底是否知道汽车在哪个门后面，从博弈论的角度来说，你都应该选择换。

只不过，有时候换有好处，有时候换没好处但也没坏处。

聪明如你可能看出来了，这有点儿像前面的抓酒鬼，但是主持人这个角色的引入，让“概率权”的概率更加生动了。

我继续用零公式的方式，来解释这一道题。更重要的是，用此题来呈现：

意识改变现实世界（的概率）。

三门问题，我以自己的方式将其描绘如下：

主持人打开B门，门后面没有汽车，理论上这是一个观察动作，带来了更多信息，理论上会改变概率，是吗？

并不全是。

这取决于主持人是否知道车在哪个门后面。

我们把概率树的分枝，理解为某件事情的各种可能性，用文艺的方法描述，就是一切可能存在的n个平行宇宙。

先看主持人不知道的情况。

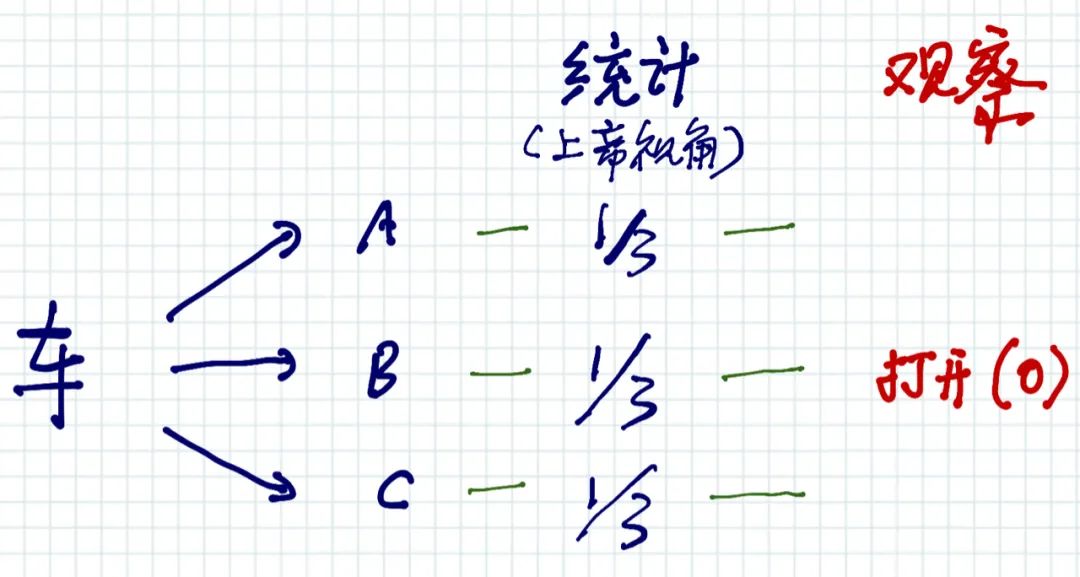
假如主持人不知道B门后面有没有汽车，那么他随机打开B门并发现是羊，只是关掉了“B门后面是汽车”的平行世界；
原来属于B的平行宇宙的“地盘”，将被平均分配给A和C，这一公平是由主持人的“未知”和这个世界的“随机”所赋予的。

如下图：

再看主持人知道的情况。

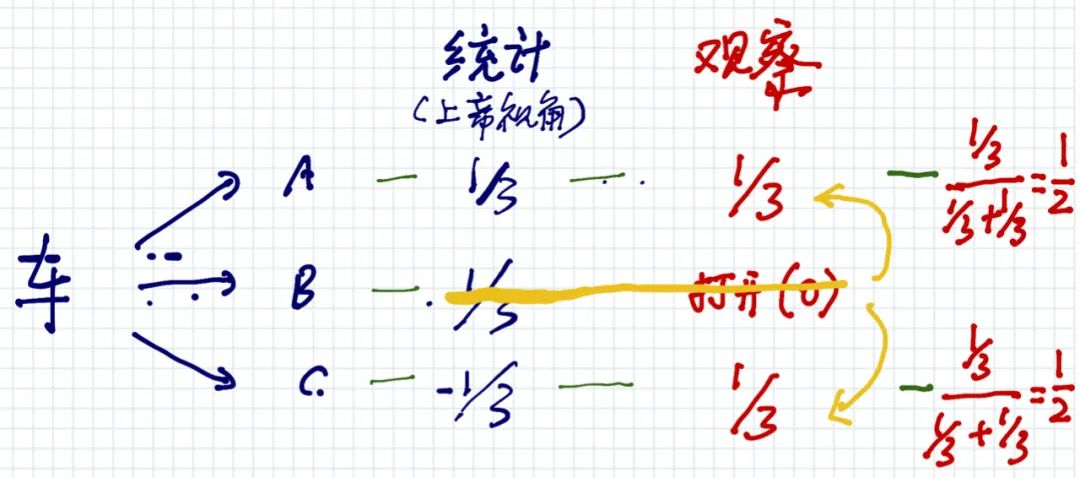
当他打开B门，其实是一个选择的结果。因为如果B门后有车，他就会选择打开C门。
所以，他打开B门，并没有产生观察者效应，也就是说没有让A门的概率由1/3变成1/2。
他主动选择了关掉B门后面1/3有车可能性的平行世界，并将其概率赋予给了C门，使其概率由1/3增加到了2/3。

如下图：

在这个案例里，我所创造的“概率权”一词，不再是一种隐喻，而是精确且生动地参与到计算中了。

不知道你是否还记得本文开始的那个问题：

你相信意识可以移动物体吗？

重新分配了概率权的主持人，是不是相当于“移动”了门后的汽车呢？

以上不厌其烦的“简单”计算，是为了从可感知的层面理解如下两点：

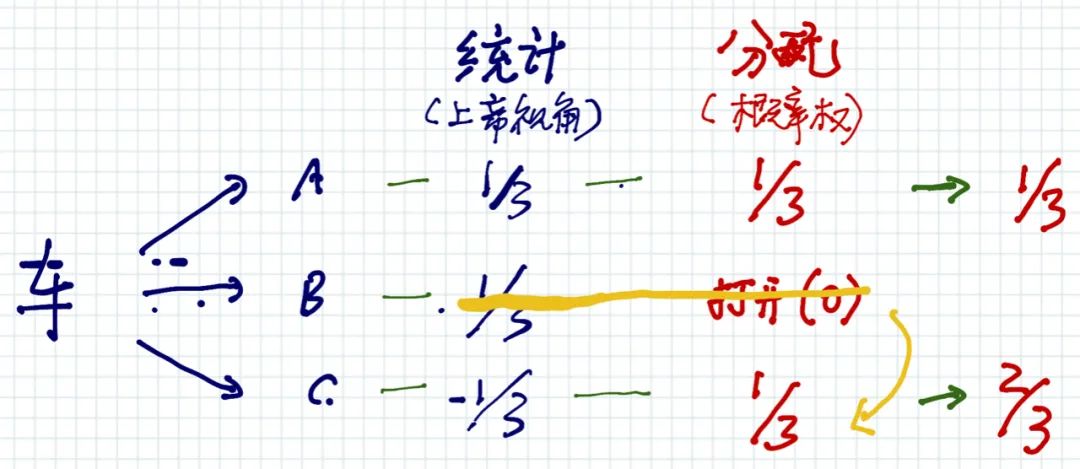
带来有价值信息的观察，改变概率的分布；
基于概率权分配概率。

这是两个很好玩儿的思考。

这是我作为业余人士的优势所在，我可以自由地去思考这些问题，尤其是这些把专业人士也绕晕了的问题。

我试图将概率与直觉建立起某些联系，这需要借助于物理来思考。

如果说主持人打开B门，引入了额外的信息，那么，该额外信息到底是如何“做功”的？

做功是能量由一种形式转化为另一种的形式的过程。

做功的两个必要因素：作用在物体上的力和物体在力的方向上通过的距离。

经典力学的定义是：当一个力作用在物体上，并使物体在力的方向上通过了一段距离，力学中就说这个力对物体做了功。

主持人知道信息，和不知道信息，其“做功”的差别是什么？

概率到底是客观存在的事物？还是主观想象的事物？

即：概率究竟存在于现实，还是存在于人的大脑？

人的主观意识，会改变这个客观世界吗？

上述问题吸引我的是，观察者的参与（本来是作为“果”），对于现实概率（本来是作为“因”）的影响。

既然叫“因果”，为什么“果”会改变“因”？

量子力学层面的观察者效应，与经典物理世界的“可能性”的观察者效应，都是围绕“概率”展开。

本文中写到的几个有争议的题目，歧义产生于“上帝视角”和“观察者视角”。

“上帝视角”研究的是样本空间；
“观察者视角”则是贝叶斯更新。

引入先验概率、后验概率、条件概率也许可以让计算更简单，但对于消除歧义并无帮助。

因为以上争议，往往在专业人士之间会更加激烈。

然而，作为一个好奇的业余爱好者，我并不打算停留于此。

雅各布·布鲁诺夫斯基在《知识与想象之起源》中说：当我们对世界的感知方式在本质上发生了如此大的变化时，继续讨论“世界是什么”，真的毫无意义。

作者认为：我们对世界的看法不是“世界是什么”，而是“人类如何看待世界”。

长久以来，人类都坚信，世界是客观存在的，它就在那儿，就是那个样子，我们的感知模式对我们解释这个“现实世界”的方式影响不大；我们可以了解世界的本质而不必担心我们使用的“工具”。

然而，雅各布·布鲁诺夫斯基认为，上面的想法是错的。

在这本出版于上个世纪70年代的书里，作者将人类称为“生物引擎”，而引擎的感知模式对于我们对世界的阐释至关重要。

当然，也应该包括我在本文反复提及的“观察”。

我们看这个世界，听这个世界，理解这个世界，都是经由“引擎”的感知。

上述思考，起源于康德在18世纪60年代提出的基本思想：

我们对外部世界的认识取决于我们的感知模式。

不久之后，康德放弃了自己的想法，转而相信牛顿的绝对空间，他提出“空间确实存在，事件必须与之相适应，我们必须先天地意识到它”。

有趣的是，爱因斯坦在13岁就开始喜欢上康德的著作，并由此开始研读休谟和马赫的著作。

年轻时，爱因斯坦阅读了很多探索科学与哲学的交界的著作。这其中，对他影响最大的是休谟。

休谟对一切不能直接由感官感知的知识都表示怀疑（一个聪明而可爱的杠精）。

在爱因斯坦看来，休谟清楚地认识到，像因果性这样一些概念并不能通过逻辑方法从我们的经验知觉中导出。

（这就是为什么我对于本文几道题目的计算，避免用成熟的公式，而是用可感知的方式去推理。）

然而，不久后，爱因斯坦开始质疑康德关于分析性真理和综合性真理之间的严格区分。

例如，一个看起来是纯粹分析的命题“三角形内角和等于180度”在非欧几何或在弯曲空间中（比如广义相对论所处理的情况）竟然是错误的。“这些概念并不包含康德赋予它们的确定性和内在必然性。”

（上述内容来自《爱因斯坦传》。）

马赫启发爱因斯坦的，不仅有“坚不可摧的怀疑态度和独立性”，更有他对牛顿的“绝对时间”的怀疑。

在爱因斯坦看来，马赫哲学的本质是：

只有当概念所指涉的对象以及概念同这些对象据以对应起来的规则能够被显示出来时，概念才是有意义的。

换句话说，要想让一个概念有意义，就需要对它进行一种操作定义。

几年以后，这种看法将为爱因斯坦带来丰硕的回报，他和贝索谈论了什么样的观察能够给两个事件“同时”发生这一看似简单的概念赋予意义。

——《爱因斯坦传》

爱因斯坦抛弃了那些“与经验没有关联”的概念，比如“绝对同时性”和“绝对速度”。

相对论告诉我们：

对时间（包括延续和同时性）的测量是相对的，它取决于观察者的运动，因此对空间（比如距离和长度）的测量也是相对的。
然而两者之间的一种联合，即所谓的“空-时”，却在任何惯性系中都保持不变。

最后

我们对这个世界的感官印象，是由神经系统进行解释和构建的。

理论上，人类的基本结构相同，我们对外部世界的观察和理解应该大致相同。

但事实并非如此。

例如当年在赤壁，面对一样的风景，苏东坡与友人看见了完全不一样的世界。

那是公元1082年，苏东坡与友人泛舟于赤壁下游玩。

清风徐来，水波不兴；白露横江，水光接天。一时间，他飘飘乎如遗世独立，羽化而登仙。

这时，客人中有吹洞箫者，倚歌而和之，其声呜呜然，如怨如慕，如泣如诉。

苏东坡问他为什么如此哀愁。

客人说：

“月明星稀，乌鹊南飞”是曹孟德的诗吧？眼前壮丽景色，都是他战斗过的地方。曹操如此牛逼，固一世之雄也，而今又在何处呢？

随后，苏东坡写出了传颂千古的诗句。

这些话语充满了现代型。对于观察这个世界的智慧，对于经验知觉，苏东坡、休谟、康德、马赫、爱因斯坦们把酒言欢。

苏东坡说道：

你可也知道这水与月？时间流逝就像这水，其实并没有真正逝去；时圆时缺的就像这月，终究没有增减。可见，从事物易变的一面看来，那么天地间万事万物时刻在变动，连一眨眼的工夫都不停止；而从事物不变的一面看来，万物同我们来说都是永恒的，又有什么可羡慕的呢？

何况天地之间，万物各有主宰者，若不是自己应该拥有的，即使一分一毫也不能求取。只有江上的清风，以及山间的明月，听到便成了声音，进入眼帘便绘出形色，取得这些不会有人禁止，感受这些也不会有竭尽的忧虑。这是大自然恩赐的没有穷尽的宝藏，我和你可以共同享受。

这首《赤壁赋》写于苏轼一生最为困难的时期之一，全篇豪放清朗，行歌笑傲。

惟江上之清风，与山间之明月，耳得之而为声，目遇之而成色，取之无禁，用之不竭。

苏东坡此赋，不正是量子时代物理学家们的世界观吗？

哥本哈根解释要求在观察者存在的情况下，波函数魔术般地发生坍塌，现实世界因此呈现。

问题在于，谁来观察宇宙呢？

宇宙是自我包含的。它包含所有事物，所以并不存在外部观察者来注意宇宙的存在。

格里宾倾向于“唯我论”者的论断。这个论断说，在宇宙中只有一个观察者，那就是我自己。“我的观察”就是使现实从量子可能性的网络中固化出来的所有重要因素。

也许，充满好奇心地观察这个世界，不仅是我们参与“现实”世界的惟一方式，也是我们“拥有”整个世界的惟一可能。

延伸阅读👇

延伸阅读《世界观》（原书第3版）

推荐语：《读者》年度十大影响力图书，新版近8万字修订，中科院自然科学史专家李明洋老师专业审阅，认知、阅读体验双重升级。《返朴》、傅盛、廖祥忠、吴国盛、陈春花等力荐。

干货直达👇

终于有人把用户画像的流程、方法讲明白了
终于有人把数据安全讲明白了
35岁的程序员，真的要转管理吗？
数据中台、标签、数据资产相关的15个名词解释

更多精彩👇

在公众号对话框输入以下关键词

查看更多优质内容！

PPT | 读书 | 书单 | 硬核 | 干货 | 讲明白 | 神操作

大数据 | 云计算 | 数据库 | Python | 爬虫 | 可视化

AI | 人工智能 | 机器学习 | 深度学习 | NLP

5G | 中台 | 用户画像 | 1024 | 数学 | 算法 | 数字孪生

据统计，99%的大咖都关注了这个公众号

👇