Datawhale干货 

作者：吴恩达，来源：新智元

【导读】吴恩达最近发布了一篇博客，介绍了几个基础算法的起源和直观理解，还宣传了一下自己重置版机器学习课程：目的竟是为了复习一遍！

神经网络模型在学术界和工业界都处于绝对的垄断地位，使得「机器学习」几乎要跟「深度学习」划上等号了。

 

作为深度学习的领军人，吴恩达自然也是深度学习的忠实使用者。

 

最近吴恩达在博客网站上发表了一篇特刊，表示自己由于常年使用神经网络，已经快忘了该怎么用传统的机器学习算法了！

 

因为深度学习并非在所有场景下都好用，所以在「盲目」使用神经网络受挫后，痛定思痛，写了一篇文章，为一些传统的机器学习算法提供一些直观上的解释。

 

 

线性回归

 

线性回归（Linear regression）可能是机器学习中的最重要的统计方法，至于谁发明了这个算法，一直争论了200年，仍未解决。

 

1805年，法国数学家勒让德（Adrien-Marie Legendre）在预测一颗彗星的位置时，发表了将一条线拟合到一组点上的方法。天体导航是当时全球商业中最有价值的科学，就像今天的人工智能一样。

 

四年后，24岁的德国天才数学家高斯（Carl Friedrich Gauss）坚持认为，他自1795年以来一直在使用这种方法，但他认为这种方法太过琐碎，无法写出来。高斯的说法促使Legendre发表了一份匿名的附录，指出「一位非常有名的几何学家毫不犹豫地采用了这种方法」。

 

这类长期存在发明争议的算法都有两个特点：好用，且简单！

 

线性回归的本质上就是斜率（slopes）和截距（biases，也称偏置）。

 

当一个结果和一个影响它的变量之间的关系是一条直线时，线性回归就很有用。

 

例如，一辆汽车的油耗与它的重量呈线性关系。

 

 

一辆汽车的油耗y和它的重量x之间的关系取决于直线的斜率w（油耗随重量上升的陡峭程度）和偏置项b（零重量时的油耗）：y=w*x+b。

 

在训练期间，给定汽车的重量，算法预测预期的燃料消耗。它比较了预期和实际的燃料消耗。然后通过最小二乘法，使平方差最小化，从而修正w和b的值。

 

考虑到汽车的阻力，有可能产生更精确的预测。额外的变量将直线延伸到一个平面。通过这种方式，线性回归可以接收任何数量的变量/维度作为输入。

 

线性回归算法在当年可以帮助航海家追踪星星，后来帮助生物学家（特别是查尔斯-达尔文的表弟弗朗西斯-高尔顿）识别植物和动物的遗传性状，进一步的发展释放了线性回归的潜力。

 

1922年，英国统计学家罗纳德-费舍尔和卡尔-皮尔逊展示了线性回归如何融入相关和分布的一般统计框架，再次扩大了其适用范围。

 

近一个世纪后，计算机的出现为其提供了数据和处理能力，使其得到更大的利用。

 

当然，数据从来没有被完美地测量过，而且多个变量之间也存在不同的重要程度，这些事实也刺激了线性回归产生了更复杂的变体。

 

例如，带正则化的线性回归（也称为岭回归）鼓励线性回归模型不要过多地依赖任何一个变量，或者说要均匀地依赖最重要的变量。如果你要追求简化，使用L1的正则化就是lasso回归，最终的系数更稀疏。换句话说，它学会了选择具有高预测能力的变量，而忽略了其他的变量。

 

Elastic net结合了两种类型的正则化，当数据稀少或特征出现关联时，它很有用。

 

神经网络中最常见的一种神经元就是线性回归模型，往往后面再跟着一个非线性激活函数，所以线性回归是深度学习的基本构件。

 

Logistic回归

 

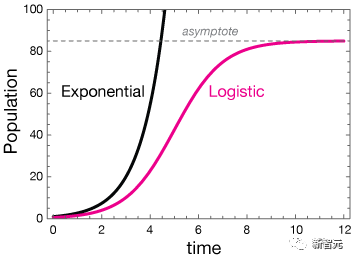
Logistic函数可以追溯到19世纪30年代，当时比利时统计学家P.F. Verhulst发明了该函数来描述人口动态。

 

随着时间的推移，最初的爆炸性指数增长在消耗可用资源时趋于平缓，从而形成了Logistic曲线。

 

 

一个多世纪后，美国统计学家威尔逊（E. B. Wilson）和他的学生简-伍斯特（Jane Worcester）设计了逻辑回归算法，以计算出多少给定的危险物质会致命。

 

Logistic回归将logistic函数拟合到数据集上，以预测在某一事件（例如，摄入马钱子）发生特定结果（例如，过早死亡）的概率。

 

 

1、训练时水平地调整曲线的中心位置，垂直地调整其中间位置，以使函数的输出和数据之间的误差最小。

 

2、将中心向右或向左调整意味着需要更多或更少的毒药来杀死普通人。陡峭的坡度意味着确定性：在中间点之前，大多数人都能活下来；超过中间点，那就说得再见了。一个平缓的斜率更宽容：低于曲线的中间点，超过一半的人可以存活；更远的地方，不到一半。

 

3、设置一个阈值，比如说0.5，曲线就成了一个分类器。只要把剂量输入模型，你就会知道你应该计划一个聚会还是一个葬礼。

 

Verhulst的工作发现了二元结果的概率，后来英国统计学家David Cox和荷兰统计学家Henri Theil在20世纪60年代末独立工作，将逻辑回归法用于有两个以上类别的情况。

 

Logistic函数可以描述多种多样的现象，并具有相当的准确性，因此Logistic回归在许多情况下提供了可用的基线预测。

 

在医学上，它可以估计死亡率和疾病的风险；在政治中，它可以预测选举的赢家和输家；在经济学中，它可以预测商业前景。

 

在神经网络中，有一部分神经元为Logistic回归，其中非线性函数为sigmoid。

 

梯度下降

 

想象一下，在黄昏过后的山区徒步旅行，你会发现除了你的脚以外看不到什么。而你的手机没电了，所以你无法使用GPS应用程序来寻找回家的路。

 

你可能会发现梯度下降的方向是最快路径，只是要小心不要走下悬崖。

 

1847年，法国数学家Augustin-Louis Cauchy发明了近似恒星轨道的算法。60年后，他的同胞雅克-哈达玛德（Jacques Hadamard）独立开发了这一算法，用来描述薄而灵活的物体的变形。

 

不过，在机器学习中，它最常见的用途是找到学习算法损失函数的最低点。

 

神经网络通常是一个函数，给定一个输入，计算出一个期望的输出。

 

训练网络的一种方法是，通过反复计算实际输出和期望输出之间的差异，然后改变网络的参数值来缩小该差异，从而使损失最小化，或其输出中的误差最小。

 

梯度下降缩小了误差，使计算损失的函数最小化。

 

网络的参数值相当于景观上的一个位置，而损失是当前的高度。随着你的下降，你提高了网络的能力，以计算出接近所需的输出。

 

不过可见性是有限的，因为在监督学习下，算法完全依赖于网络的参数值和梯度，也就是当前损失函数的斜率。

 

 

使用梯度下降，你也有可能被困在一个由多个山谷（局部最小值）、山峰（局部最大值）、马鞍（马鞍点）和高原组成的非凸形景观中。事实上，像图像识别、文本生成和语音识别这样的任务都是非凸的，而且已经出现了许多梯度下降的变体来处理这种情况。

 

K-means聚类

 

如果你在派对上与其他人站得很近，那么你们之间很可能有一些共同点。

 

K-means的聚类就是基于这种先验想法，将数据点分为多个group，无论这些group是通过人类机构还是其他力量形成的，这种算法都会找到它们之间的关联。

 

 

美国物理学家斯图尔特-劳埃德（Stuart Lloyd）是贝尔实验室标志性创新工厂和发明原子弹的曼哈顿项目的校友，他在1957年首次提出了k-means聚类，以分配数字信号中的信息，不过他直到1982年才发表。

 

与此同时，美国统计学家爱德华-福吉（Edward Forgy）在1965年描述了一种类似的方法——劳埃德-福吉算法。

 

K-means聚类首先会寻找group的中心，然后将数据点分配到志同道合的group内。考虑到数据量在空间里的位置和要组成的小组数量，k-means聚类可以将与会者分成规模大致相同的小组，每个小组都聚集在一个中心点或中心点周围。

 

在训练过程中，算法最初需要随机选择k个人来指定k个中心点，其中k必须手动选择，而且找到一个最佳的k值并不容易。

 

然后通过将每个人与最接近的中心点联系起来形成k个聚类簇。

 

对于每个聚类簇，它计算所有被分配到该组的人的平均位置，并将平均位置指定为新的中心点。每个新的中心点可能都不是由一个具体的人占据的。

 

在计算出新的中心点后，算法将所有人重新分配到离他们最近的中心点。然后计算新的中心点，调整集群，以此类推，直到中心点（以及它们周围的群体）不再移动。

 

将新人分配到正确的群组很容易，让他们在房间里找到自己的位置，然后寻找最近的中心点。

 

K-means算法的原始形式仍然在多个领域很有用，特别是因为作为一种无监督的算法，它不需要收集潜在的昂贵的标记数据，它的运行速度也越来越快。

 

例如，包括scikit-learn在内的机器学习库都得益于2002年增加的kd-trees，它能极快地分割高维数据。

参考资料：

https://read.deeplearning.ai/the-batch/issue-146/

整理不易，点赞三连↓