如何量化样本偏差对信贷风控模型的影响？
1. 信贷业务中的样本偏差来源
2. 信贷业务中的风控模型术语
3. 拒绝推断方法概述
4. 仿真实验设计评价
5. 总结
信贷业务中的样本偏差来源
信贷业务大致分为营销获客、贷前授信、贷中动支等几个环节。如图1所示，每一个环节都有一定的风控措施，用以筛选客群。在互金行业信贷业务中，目前授信通过率大致在10%～30%，其中10%+又是较为普遍的数字。因此，大约90%的客户便失去了授信资格，也就没有借款机会。
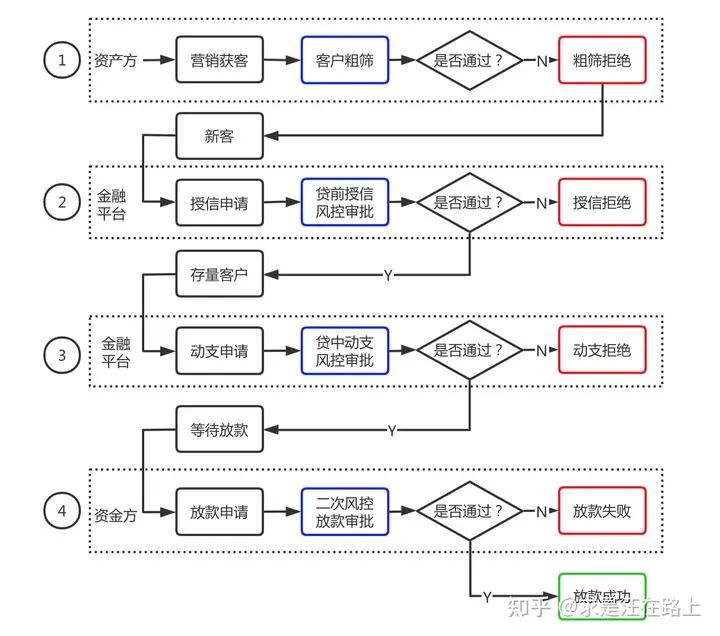
在风控模型迭代时，我们只能基于还款表现来定义样本的好坏，并组成建模样本。一些无法获知其还款表现的样本，造成了样本偏差。失去还款表现的样本主要来源自以下几类：
授信拒绝客户
授信通过但从未动支的睡眠户
动支拒绝客户
放款失败客户
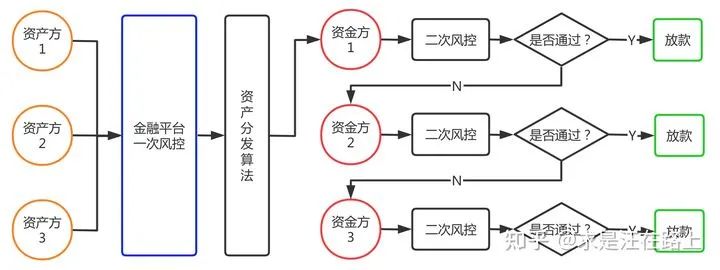
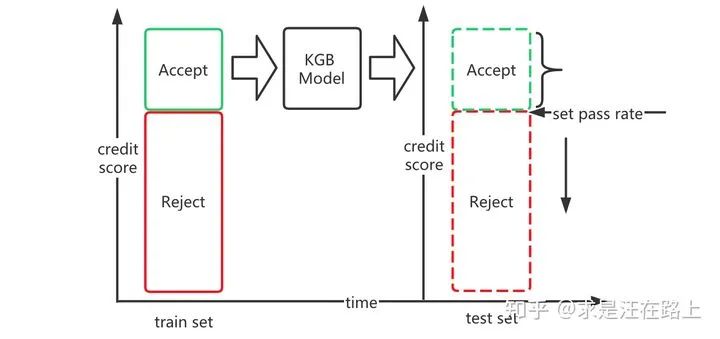
我们补充介绍图1中的二次风控业务概念。其诞生背景是，在联合贷业务中，银监会要求资金方（银行、消费金融等机构）必须承担自主风控能力，不可将核心风控交付上游资产方等第三方机构完成。上游资产方一般要求资金方的通过率不低于某个值（如80%）。
如图2所示，对于第一家资金方拒绝的借款申请订单，仍会路由给下一家，直至放款通过。因此，对于在金融平台端便拥有借款申请订单的所有贷后表现数据。
信贷业务中的风控模型术语
为提高自动化审批效率，我们在业务实践中大量借助模型来对客户排序、筛选、分群，并对不同人群制定不同的策略。大数据风控的套路都大同小异，贵在精细化运营。
模型并不神秘，其本质是从历史样本中拟合输入和输出之间的关系，并将该规律应用于新输入的预测。模型的优势在于变量含义清晰（目标变量决定了模型分数的含义），区分能力强（融合了大量弱变量的信息），能让决策更为科学。
为便于理解，我们约定特征向量 
，目标变量 
。同时，定义一些模型术语概念：
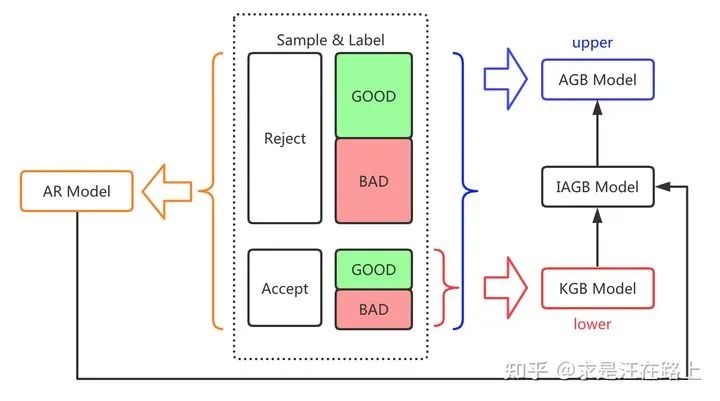
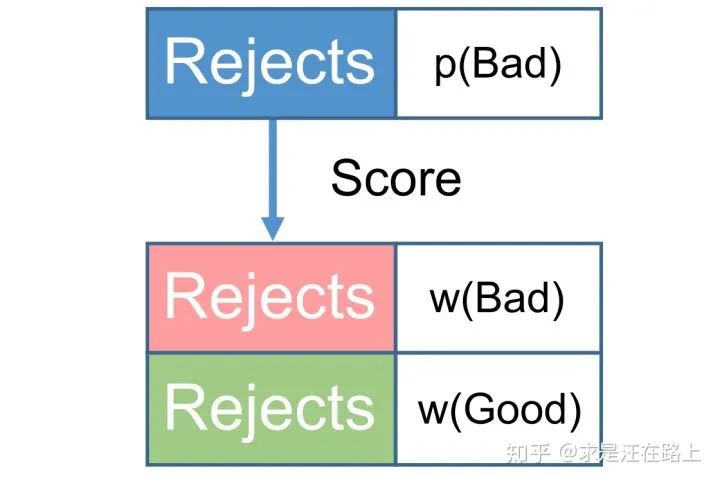
AR(Accept Reject)模型：以是否通过定义Y （1 = accept，0 = reject），以全量申请样本构建，用以预测
。KGB(Known Good Bad)模型：以是否违约定义Y （1 = bad，0 = good），以已知好坏的通过样本构建，用以预测
。AGB(All Good Bad)模型：以是否违约定义Y （1 = bad，0 = good），以已知好坏的通过样本和（假设真实已知好坏）拒绝样本联合构建，用以预测
。IAGB(Inferred All Good Bad)模型：以是否违约定义Y（1 = bad，0 = good），以已知好坏的通过样本和推断好坏的拒绝样本联合构建，用以预测
。
注意，"通过"的概念包括贷前授信申请通过、贷中借款申请通过、放款申请通过等任意一种，并不局限于授信通过。
该如何理解AR模型和KGB模型呢？
（1）AR模型刻画了金融机构对客户资质的认可度。认可度这个词比较抽象，你也可以理解为是否是目标客群。虽然当前授信策略可基于风险、收入（偿债能力）、利润等多种角度，但主流依据仍然是风险维度。因此，AR模型将线上复杂的一套风控系统进行了抽象，对风险也具有较好的排序性。在实践中，AR模型的KS基本都能达到50%以上。
（2）KGB模型则是对AR模型在风险识别上的补充。打个比方，如果AR分在0～100分，分数越高，代表通过的概率越高。如果按历史通过的标准制定阈值，通过的标准为80分。但是，由于这个AR模型并非十全十美，在通过的客群上，我们发现仍存在一些风险较高的客户。因此，我们基于通过样本构建KGB模型，对客群再次筛选，从而不断降低通过客群的风险水平。
（3）AR模型和KGB模型在各自建模样本上是无偏的。AR模型在全量样本上是无偏的，KGB模型在通过样本上是无偏的。但是，KGB相对于全量样本是有偏的。
拒绝推断方法概述
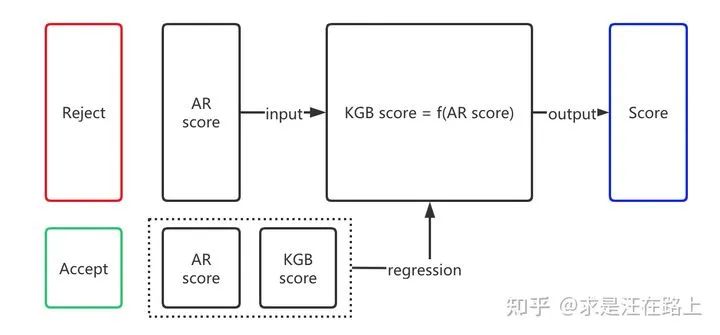
如图3所示，下限是KGB模型，上限是AGB模型，经过拒绝推断改良后的模型称为IAGB模型。于是，问题的核心在于如何引入正向信息，让IAGB模型逼近上限。我们很难评估信息是正向，还是负向的。因此，IAGB模型的性能可能会反而比不上KGB模型，这就是推断好坏标签所带来的风险。
若能准确推断每个拒绝样本的真实标签，那么IAGB模型就等于AGB模型。很可惜，现实中不可能做到这点，我们只能在KGB模型的基础上通过某些方法将其修正为IAGB模型。
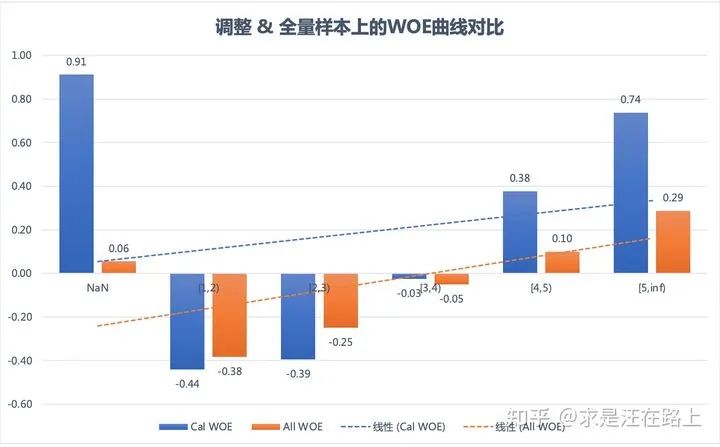
为更直观理解这一点，我们假设只采用一个多头借贷变量来建立模型。理由是，多头变量是相对客观，且具有明确业务含义的变量。一般情况下，多头变量取值越大，违约风险越高。这能帮助我们清晰看到差异性。
我们对放款样本和全量样本设置相同的分箱边界，统计各分箱内的WOE值，并通过线性模型拟合。如图4所示，全量样本上的WOE曲线（橙色）更为陡峭，而放款样本上的WOE曲线（蓝色）则相对平缓。这两根曲线之间的差异性，就是KGB模型与AGB模型之间差异的体现。
而如何将Accept WOE曲线修正为All WOE曲线，就是我们所要探索的核心问题。
回顾在《风控建模中的样本偏差与拒绝推断》中，我们介绍了很多拒绝推断（reject inference)方法的操作步骤。在本文中，笔者选择了3个有代表性的方法，希望从更高的视角分析背后的思想。
方案一: Re-weighting(重新加权法)
重新加权法只是调整了通过的好坏样本的权重，并没有把拒绝样本加入建模样本。基本思想包括：
为更精细赋值推断的调整因子，可将样本经过一定风险排序后，划分多个区间后，对每个区间分别赋予一个调整因子。
拒绝样本的风险高于通过样本，这意味着调整因子都大于1。在当前风控系统有效的前提下，该假设成立。
其操作步骤为：
在通过样本上构建KGB模型，并对全量样本打分
。将全量样本按
降序排列，等频分箱，统计每个箱中通过和拒绝样本数。计算每个分箱中通过的好坏样本的权重
引入样本权重，利用通过好坏样本重新构建KGB模型。
符号含义可参考下表。
利用该方法，我们对WOE值进行调整，得到图5。对比图4和图5，可以发现相对于Accept WOE曲线，Cal WOE曲线与All WOE曲线更为接近。说明拒绝推断后的模型效果确实带来一定的改善。
方案二: 模糊展开法
由于KGB模型在通过样本上是无偏的，我们只需要对拒绝样本进行一定的修正。如果说直接赋予0或1的标签，推断失误的风险较大。那么，我们就引入权重项来模糊表达。基于以上思想，其操作步骤为：
在通过样本上构建KGB模型，得到
，并对拒绝样本打分。将每条拒绝样本复制为不同类别，不同权重的两条：一条标记为1，权重为
。另一条标记为0，权重为 
；利用变换后的拒绝样本和放贷已知好坏样本（类别不变，权重设为1）建立AGB模型。
方案三: 两阶段法（双评分卡）
根据全概率公式，我们可以将 表达为：
其中：
，这是AR模型的预测结果。- ，这是KGB模型的预测结果。
因此，如果能获知 
，也就是根据拒绝样本也构建一个"KGB"模型，问题便可迎刃而解。
根据式（1）可知，IAGB模型相对于KGB模型而言，唯一可以带来增量信息的便是AR模型分。AR分是唯一连接通过样本和拒绝样本之间的桥梁。我们需要思考该如何利用这部分信息。
如图7所示，AR分和KGB分在通过样本上都是无偏的，因此可在通过样本上回归拟合两者的关系，得到 
。我们将得到的回归函数 
应用在拒绝样本上。
但这个函数仍然是有偏的，因为其仍然只用到了通过样本上的信息。因此，接下来我们再利用模糊展开法建立AGB模型。
仿真实验设计评价
这些拒绝推断方法可能大家都已经熟悉，最大的疑惑在于——既然拒绝样本都失去表现，那如何实践验证效果呢？打开思维的束缚，样本偏差是相对的，任何样本集经过排序后总能创造出偏差条件。
借鉴二次风控的做法，我们可以在放款通过的样本上构建实验。对于满足足够长的还款表现期的放款样本，都拥有已知的贷后表现。我们一共设计了3个实验。
实验一：验证样本偏差对KGB模型的影响。
1. 将100%的放款样本作为全量总体，只考虑历史训练的风险分（online score）当作线上风控系统唯一的决策变量，对样本进行排序，并设置通过率为30%（或其他比例），人为制造样本偏差。事实上风控系统是一个特别复杂的系统，包括客群细分策略、资信数据查询策略等。这里抽象为一个模块以简化流程。
2. 利用2020年5～6月通过的30%样本（训练集）建立KGB模型，并在2020年7～8月（测试集）上进行评估，作为模型上线应用的模拟。
3. 在2020年7～8月（测试集）上，根据online_score排序后，设置不同的通过率（30% ～ 100%），并用KGB模型在通过样本上测算KS，观察KS的效果变化。
事实上，前文中所说的通过样本和全量样本也都是如此设计而来。
如图8所示，以上操作步骤真实反映了我们日常迭代KGB模型的过程，即每次都只能在通过样本上构建模型，并在通过样本上验证模型效果。实验结果如图9所示。为了量化样本偏差的影响，我们采用KS和PSI两项指标。
KS指标：衡量模型对好坏的区分度。由于测试集上全量样本都有已知的好坏标签，对于通过客群计算KS。KS越大，代表模型区分度越好。
PSI指标：衡量模型应用样本相对于建模样本的分数偏差。PSI越大，说明样本群体分数分布差异性越大。
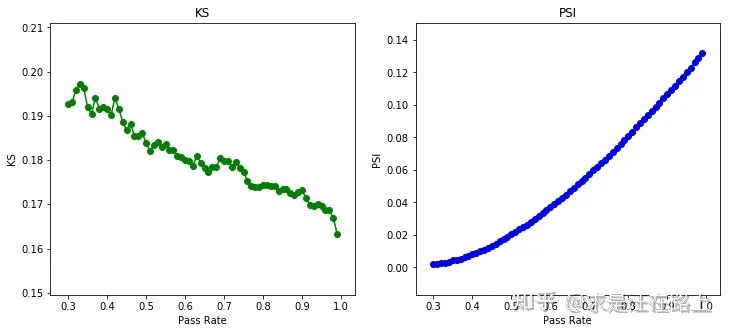
我们发现，在对标30%的通过样本上，模型的KS达到最高（19%～20%），而随着样本偏差增大，KS开始下降，直至16%。这个现象说明：
如果只是利用KGB模型的排序性，拒绝推断并不是必需环节，因为作用到全量样本上，虽然KS会下降，即便我们不知道衰减程度有多大，但可能仍然具有一定区分度。
将上述结论进一步推广：在头部优质客群上所建立的模型，在全量客群上效果自然会衰减。这解释了用单一机构的Y所建立的KGB模型，在其他机构上可能完全失效的现象。如果你测试过三方数据商提供的评分产品，你就会有更深的体会。
实验二：探索AR与KGB模型混合使用方法。
模型设计时一定要预先考虑使用场景。在模型应用环节，我们提出了3种方案：
（1）AR模型和KGB模型交叉使用，组成联合分布，筛选出目标客群。这是因为AR模型学到了历史风控系统的经验，拒绝样本一般比通过样本风险更高，因此AR模型对好坏仍然具有一定的排序性。事实上，这是目前风控策略同学使用最多的方法。
（2）AR模型预筛出最好的部分客群，KGB模型在这部分客群上作用。我们假设AR模型可以预先帮助KGB模型减少样本偏差。该方案的合理性在于，如果授信通过率为10%，那么根据AR分数便可拦截70%的人群，对于剩余的30%人群，我们再利用KGB模型进行排序。
（3）利用拒绝推断技术，将AR模型和KGB模型融合为一个IAGB模型分。接下来再利用IAGB模型分进行决策。
实验三：探索利用拒绝推断技术构建IAGB模型。
在实践中，我们尝试使用各类方法，但是由于样本、特征等差异性，实验结果可能并不可靠，这里并不展示实验结果。但是，笔者更为推荐大家利用两阶段双评分卡来进行拒绝推断探索。
在真实业务中，除了二次风控外，在贷前授信环节我们确实没有Y数据。此时可以通过阈值外的间谍样本（spy）进行评估效果。
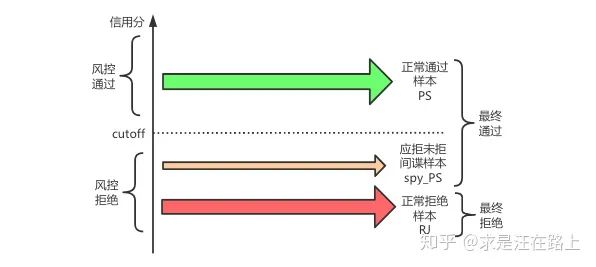图 11 - 申请订单的3种状态
总结
针对真实信贷业务中存在的样本偏差问题，本文对以下几个问题提出了一些参考解决方案。
如何根据真实业务场景，创造样本偏差条件？
如何验证样本偏差对KGB模型的影响？
如何验证拒绝推断方法的有效性？
AR模型和KGB模型如何协同决策？
任何科学决策都离不开数据支持，拒绝推断的难点存在于多个方面：
在某些场景下，拒绝样本的真实标签缺失，造成效果好坏评估上的不可能。
很多方法都有潜在的假设，需要试凑法来多次实验，很难总结出固定的方法论。
但是，我们总是希望获取更多的正向信息，措施包括：利用AR分、拒绝标注等。需要指出的是，本文也只是提出了一些方法论上的指导，所给出的数据结论可能并不具有普世价值。欢迎大家探索尝试！
作者：求是汪在路上（知乎ID) 上海新金融风险实验室 风控算法专家
作者知乎：https://www.zhihu.com/people/zayn-m/posts