搜索

超详细!聚类算法总结及对比!

算法进阶

共 15670字，需浏览 32分钟

 · 2024-03-29

一、聚类的简介

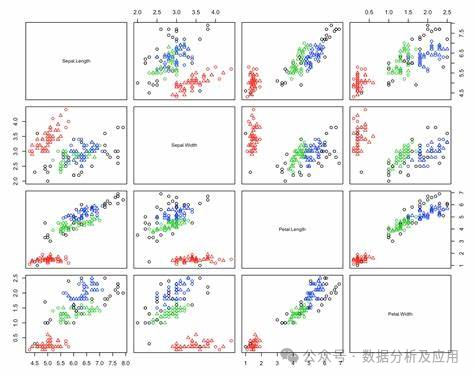
聚类分析，也称为聚类，是一种无监督的机器学习任务。与监督学习不同，聚类算法仅依赖输入数据，并致力于在特征空间中找到自然的组或群集。这些群集通常是特征空间中的密度区域，其中同一群集的数据点比其他群集更紧密地聚集在一起。

聚类在数据分析中扮演着重要角色，有助于深入了解问题域的内在结构和模式。这种分析有时被称为模式发现或知识发现，可以帮助我们洞察数据中隐藏的模式和关联。 聚类还可以作为特征工程的一种手段。通过将数据点映射到已标识的群集中，我们可以为现有和新的示例创建新的特征标签。

cf4d0f4f0e1e89f627175dc47c9e2aeb.webp

二、聚类方法汇总及对比

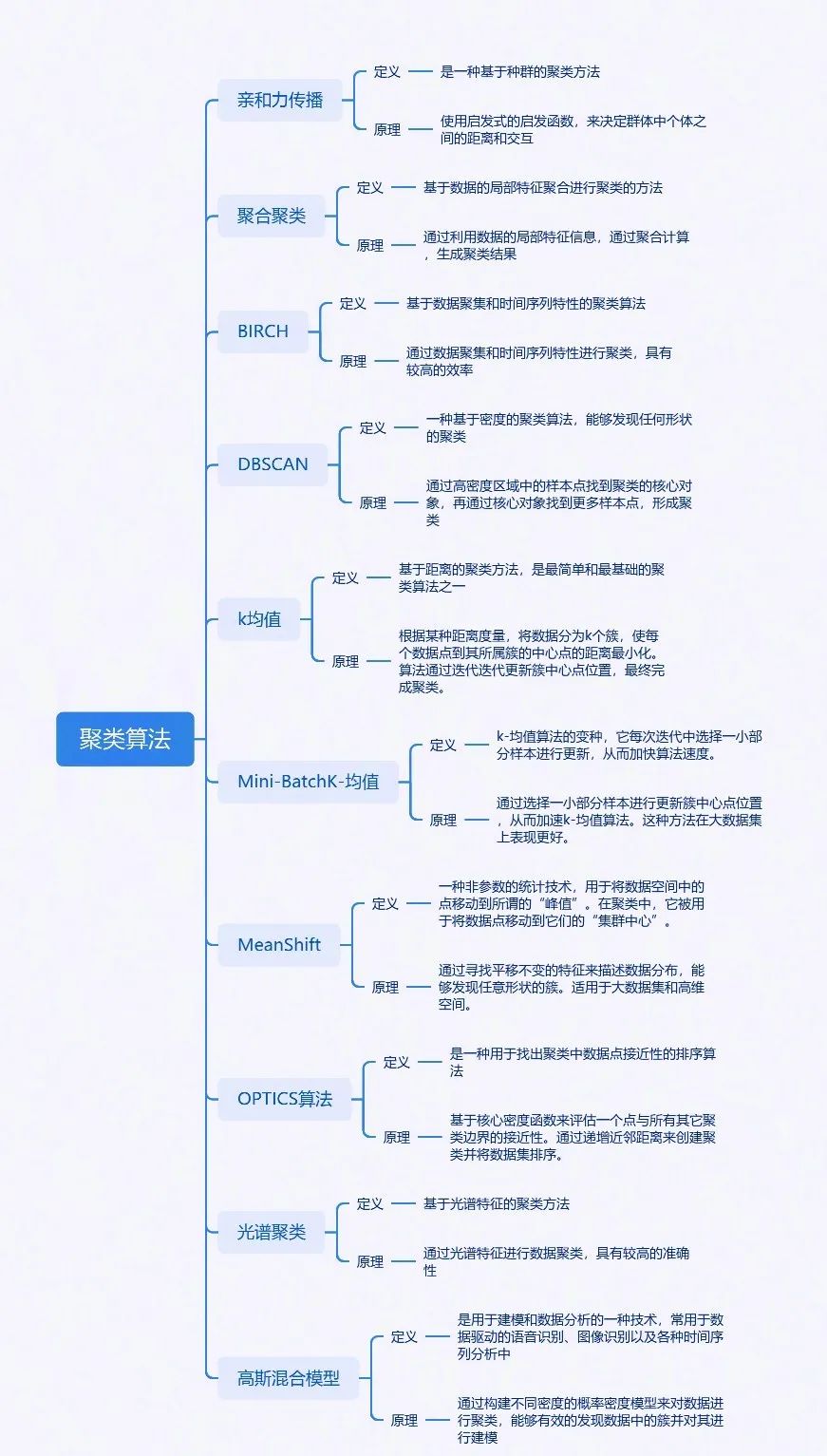
实际项目中Kmeans聚类应该是最为常用的聚类模型，但其实聚类模型的种类还挺多的，每种聚类模型都有其独特的特性和应用场景。在实际应用中，需要根据具体的数据情况、算力资源和业务需求来选择合适的模型。

b715c76b70d8f34415dddd47fa8104db.webp

  1. 亲和力传播：这是一种基于传播算法的聚类技术，通过模拟信息传播过程来实现聚类。它能够快速有效地处理大规模数据集，特别适合用于社交网络分析、推荐系统等领域。

  2. 聚合聚类：这是一种自下而上的聚类方法，通过逐步将相似的小规模对象合并为较大的簇，最终形成大规模的聚类。适合处理大规模数据集，并能够发现任意形状的簇。应用场景包括市场细分、客户分群等。

  3. BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies）：利用树结构进行快速聚类和规约数据。通过构建聚类特征树，能够快速发现数据的聚类结构。适用于大规模数据集，尤其对于具有层次结构的数据有较好的效果。应用领域包括电子商务、市场分析等。

  4. DBSCAN（Density-Based Spatial Clustering of Applications with Noise）：基于密度的聚类算法，能够将密度相连的点划分为簇，并在噪声空间数据库中发现任意形状的聚类。适用于异常检测、图像分割等领域。

  5. 模糊C-means：一种基于模糊逻辑的聚类算法，与K-means相似，但允许一个数据点属于多个簇，每个簇都有一定的隶属度或概率。适合处理具有不确定性和模糊性的数据，在市场细分、文本挖掘等领域有广泛应用。

  6. K-means：经典的基于距离的聚类算法，通过迭代计算将数据点划分为K个簇，使得每个数据点到其所在簇中心的距离之和最小。应用场景包括市场细分、客户分群等。

  7. K-medoids：改进的K-means算法，通过选取簇中位置最中心的样本点作为参照点来进行聚类。对异常值不敏感，适合处理具有较大极端值的数据集。

  8. Mean Shift：基于密度的非参数聚类算法，通过计算每个点到其他点的距离评估密度，找到密度增大的方向以发现聚类。适合处理形状不规则的簇，并能够处理噪声和异常值。应用场景包括图像分割、异常检测等。

  9. OPTICS (Ordering Points To Identify the Clustering Structure)：基于密度的聚类算法，通过计算每个点到其他点的距离评估密度，并生成排序列表以识别聚类结构。能够发现任意形状和大小的簇，并处理噪声和异常值。应用领域包括时间序列分析、图像分割等。

  10. 主题模型：用于发现数据集中潜在的主题或模式的概率模型。通过对文档集合进行建模，揭示其中的主题分布和词语关系。适用于文本挖掘、信息检索等领域。

  11. 高斯混合模型（GMM）：一种概率模型，假设数据点是从多个高斯分布中生成的。能够拟合复杂的数据分布，并给出每个数据点属于各个簇的概率。适用于时间序列分析、语音识别等领域。

  12. 谱聚类：基于图理论的聚类方法，通过构建数据的相似性矩阵并将其转化为图，然后对图进行聚类以发现数据的内在结构。能够发现任意形状的簇，并处理噪声和异常值。应用场景包括图像分割、文本挖掘等。

  13. CLIQUE（Clustering In QUEst）是一种基于网格的聚类算法，它通过将数据空间划分成多个网格单元，然后对每个网格单元进行聚类，从而发现数据的分布模式。CLIQUE算法的特点是简单、高效，适用于大规模数据集的聚类分析。它能够处理各种形状和密度的簇，并且对噪声和异常值具有较强的鲁棒性。然而，CLIQUE算法对网格单元的划分非常敏感，过细或过粗的划分可能会影响聚类的结果。

  14. STING（Statistical Information Grid）是一种基于网格统计信息的聚类算法。与CLIQUE不同，STING在每个网格单元上计算统计信息，例如均值、方差、协方差等，然后基于这些统计信息进行聚类。STING算法的特点是能够处理高维数据集，并且能够发现数据中的非线性模式。它还具有较强的鲁棒性，能够处理异常值和噪声。然而，STING算法的计算复杂度较高，需要较大的内存空间。

  15. SKWAVECLUSTER是一种基于声波聚类的算法。它利用声波传播的特性进行聚类，将声波的传播路径作为聚类的依据。SKWAVECLUSTER算法的特点是能够发现数据中的任意形状和大小的簇，并且具有较强的鲁棒性。它适用于具有复杂分布模式的数据集，例如流数据、时间序列数据等。然而，SKWAVECLUSTER算法的计算复杂度较高，需要较长的运行时间。

在工作或学习中，聚类算法是非常常见的算法之一。这里与大家剖析总结下常用的聚类算法：

1、亲和力传播 (Affinity Propagation)

模型原理

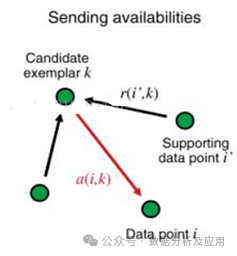
亲和力传播是一种基于实例的学习算法，用于聚类。它通过发送消息在数据点之间建立关系，并选择最佳的聚类结果。

7d19461e11ea8210a4208f610bfd5a2d.webp

模型训练

训练过程通过不断迭代，为两对数据点之间相似度的输入度量。在数据点之间交换实值消息，直到一组高质量的范例和相应的群集逐渐出现，使数据点之间形成聚类。

优点

  • 无需预先设定聚类数量。

  • 对异常值具有较强的鲁棒性。

缺点

  • 对初始参数敏感。

  • 可能产生不完整的簇。

使用场景

适用于任何需要基于实例学习的聚类任务。

Python示例代码 

    
        
          from sklearn.cluster import AffinityPropagation
        
        
          from sklearn import metrics
        
        
          from sklearn.datasets import make_blobs
        
      
        
          
            # 生成样本数据  
          
        
        
          centers = [[1, 1], [-1, -1], [1, -1]]
        
        
          X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.4, random_state=0)
        
      
        
          
            # 训练模型  
          
        
        
          af = AffinityPropagation(preference=-50).fit(X)
        
        
          cluster_centers_indices = af.cluster_centers_indices_
        
        
          labels = af.labels_
        
      
        
          n_clusters_ = len(cluster_centers_indices)
        
        
          print('Estimated number of clusters: %d' % n_clusters_)
        
        
          print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
        
        
          print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
        
        
          print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
        
        
          print("Adjusted Rand Index (ARI): %0.3f"
        
        
          % metrics.adjusted_rand_score(labels_true, labels))
        
        
          print("Adjusted Mutual Information (AMI): %0.3f"
        
        
          % metrics.adjusted_mutual_info_score(labels_true, labels))

2、聚合聚类 (Agglomerative Clustering)

模型原理

聚合聚类是一种自底向上的聚类方法。它从数据点（或称为观测值）的集合开始，然后将这些点视为初始的簇。接着，算法逐步合并这些簇，直到满足某个停止条件，如达到预设的簇数量或达到某个特定的簇大小。在这个过程中，算法通过计算簇之间的距离来确定哪些簇应该被合并。

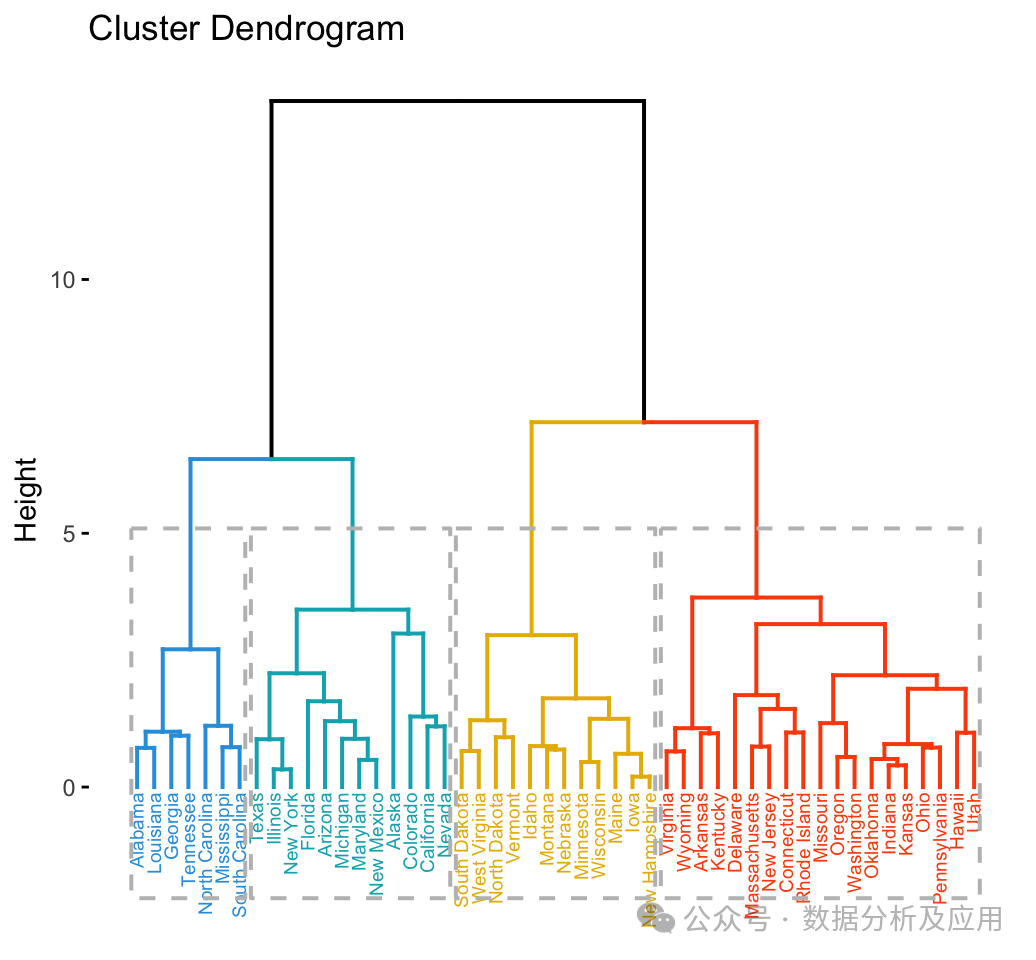
352b693fffc30da0aca2c4b8a88ada94.webp

模型训练

  1. 初始化：每个数据点被视为一个簇。

  2. 合并：根据某种距离度量（如欧氏距离、余弦相似度等），将最近的簇合并为一个新的簇。

  3. 重复：重复步骤2，直到满足停止条件。

  4. 输出：返回合并后的簇结果。

优点

  • 层次结构：能够生成数据的层次结构或嵌套聚类，这在某些应用中非常有用。
  • 可解释性：由于是自底向上的方法，可以更容易地解释和可视化结果。

  • 处理大型数据集：由于不需要一次性处理所有数据，因此可以有效地处理大型数据集。

缺点

  • 时间复杂度： 随着数据集规模的增加，时间复杂度可能会迅速增加。

  • 不平衡簇： 可能产生不平衡的簇，即某些簇包含大量数据点，而其他簇则包含很少的数据点。

  • 初始化敏感： 对初始化的选择敏感，可能会导致不同的聚类结果。

使用场景

  • 层次聚类：适用于需要层次结构的聚类任务，如市场细分或社交网络分析。
  • 异常检测：可以通过观察聚类结果中的离群点来检测异常值。

  • 数据预处理：在某些机器学习任务中，可以使用聚合聚类作为预处理步骤来简化数据或提取特征。

Python示例代码（使用scikit-learn库）: 

    
        
          from sklearn.cluster import AgglomerativeClustering  # 导入AgglomerativeClustering类    
        
        
          from sklearn import datasets  # 导入datasets用于生成样本数据    
        
        
          from sklearn.preprocessing import StandardScaler  # 导入StandardScaler进行标准化处理    
        
        
          import matplotlib.pyplot as plt  # 导入绘图库

‍ 

      
        
          # 生成样本数据    
        
      
      
        iris = datasets.load_iris()  # 使用Iris数据集作为示例    
      
      
        X = iris["data"]  # 提取特征矩阵    
      
    
      
        
          # 数据标准化    
        
      
      
        scaler = StandardScaler()
      
      
        X = scaler.fit_transform(X)  # 对数据进行标准化处理    
      
    
      
        
          # 设置聚类数    
        
      
      
        n_clusters = 2  # 根据需求设置聚类数    
      
      
        
          # 创建AgglomerativeClustering对象并拟合数据    
        
      
      
        clustering = AgglomerativeClustering(n_clusters=n_clusters)
      
      
        labels = clustering.fit_predict(X)  # 获取每个样本点的聚类标签    
      
      
        
          # 可视化结果    
        
      
      
        
          plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  # 使用viridis色彩映射绘制结果图    
        
      
      
        plt.show()  # 显示结果图  ```

3、BIRCH 聚类模型

模型原理

BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies）是一种基于层次的聚类方法。它通过构建一个聚类特征树（Clustering Feature Tree，CF Tree）来组织和存储数据点，并利用该树进行聚类。BIRCH的核心思想是利用聚类特征（Clustering Feature，CF）来描述数据点的聚类信息，并通过逐步合并最相似的聚类对来形成层次聚类。

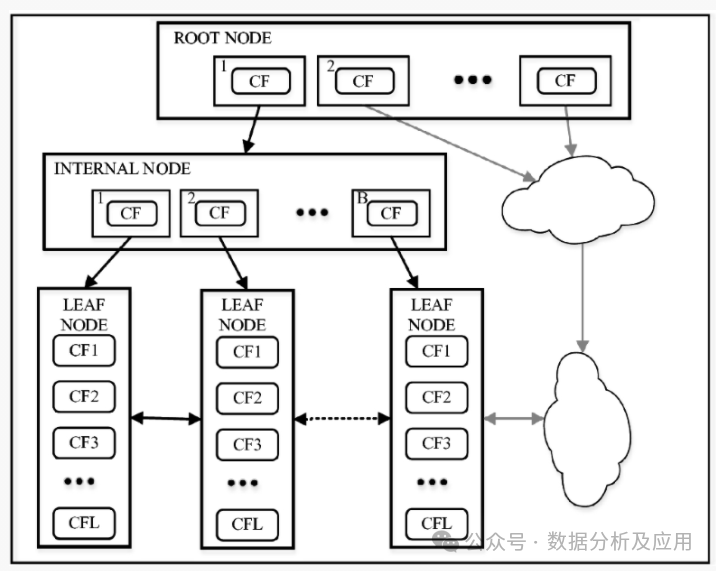
9e42bf33f98aa1cbe8e8a0208e69dda1.webp

模型训练

  1. 初始化：为每个数据点创建一个聚类特征（CF）。

  2. 合并：根据相似度度量，合并最相似的CF对。

  3. 重复：重复步骤2，直到满足停止条件（如达到预设的簇数量或达到某个特定的簇大小）。

  4. 输出：返回合并后的簇结果。

优点

  • 高效性：对于大规模数据集，BIRCH具有较高的效率。
  • 可扩展性：由于其基于树的存储结构，BIRCH在处理大量数据时具有良好的可扩展性。

  • 灵活性：能够处理不同类型的数据，包括非数值型数据。

缺点

  • 参数敏感性：BIRCH对参数的选择较为敏感，如CF树的构建参数和相似度度量方法等。
  • 不平衡簇：可能产生不平衡的簇，尤其是当数据分布不均时。

  • 计算复杂度：对于高维数据，BIRCH的计算复杂度可能较高。

使用场景

  • 大规模数据集：BIRCH适用于处理大规模数据集，特别是那些需要高效和可扩展聚类的场景。
  • 多维数据：适用于处理多维特征的数据，能够有效地处理非数值型数据。

  • 层次聚类：适用于需要层次结构的聚类任务，如市场细分或社交网络分析。

Python示例代码（使用pyclustering库）: 

    
        
          from pyclustering.cluster.birch import birch  # 导入BIRCH聚类算法    
        
        
          from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer  # 导入中心初始化器    
        
        
          from pyclustering.samples.definitions import FCPS_SAMPLES  # 导入样本数据集    
        
        
          from pyclustering.utils import read_sample  # 导入读取样本数据的工具    
        
        
          from pyclustering.view.gplot import gplot  # 导入绘图库    
        
        
          from pyclustering.view.dendrogram import dendrogram  # 导入层次聚类结果的显示工具    
        
        
          from pyclustering.metrics.pairwise import euclidean_distance  # 导入欧氏距离度量函数    
        
        
          import matplotlib.pyplot as plt  # 导入绘图库    
        
        
          import numpy as np  # 导入numpy库进行数组操作    
        
      
        
          
            # 读取样本数据集[two_diamonds]    
          
        
        
          sample = read_sample(FCPS_SAMPLES.SAMPLE_TWO_DIAMONDS)
        
        
          
            # 使用K-Means++初始化方法为BIRCH算法生成中心点（两个中心点）    
          
        
        
          initial_centers = kmeans_plusplus_initializer(sample, 2).initialize()
        
        
          
            # 创建BIRCH聚类对象并使用中心点初始化其内部结构    
          
        
        
          birch_instance = birch(sample, initial_centers, dist_metric=euclidean_distance)
        
      
        
          
            # 执行聚类操作    
          
        
        
          birch_instance.process()
        
        
          
            # 获取聚类结果    
          
        
        
          clusters = birch_instance.get_clusters()  # 获取簇的索引列表    
        
        
          
            # 可视化结果    
          
        
        
          gplot(birch_instance.get_data(),BirchDataVisualizer(clusters),'birch')  # BirchDataVisualizer是用于可视化BIRCH数据的自定义工具类  ```

4、DBSCAN 聚类模型

模型原理

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类方法。它的主要思想是：一个簇是由一个密度足够大的区域所组成的，并且这个区域是核心对象所连接的稠密区域。DBSCAN将簇定义为具有足够高密度的区域，并且通过噪声点将簇与相邻的密度区域分开。

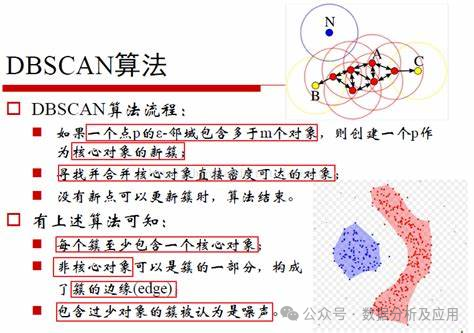
f8c01c377afb5c36acbb82a6b88ab3bb.webp

模型训练

  1. 初始化：选择一个未被访问过的点作为当前点。
  2. 密度估计：如果当前点的ε-邻域内的点数量大于等于MinPts，则当前点为核心点。否则，当前点为噪声点。
  3. 扩展簇：从核心点开始，将其标记为簇的一部分，并递归地访问其ε-邻域内的所有点。如果某个点的ε-邻域内的点数量大于等于MinPts，则该点为核心点，并将其标记为已访问。
  4. 重复：重复步骤2和3，直到所有点都被访问。

  5. 输出：返回所有簇的结果。

优点

  • 密度敏感：能够发现任何形状的簇，并处理异常值和噪声。
  • 可扩展性：对于大规模数据集，DBSCAN具有较好的可扩展性。

  • 无需预设簇数量：与其他基于距离的聚类方法相比，DBSCAN不需要预设簇的数量。

缺点

  • 参数敏感：对参数ε和MinPts的选择较为敏感，不同的参数值可能会导致不同的聚类结果。
  • 计算量大：对于高维数据，DBSCAN的计算量可能会很大。

  • 对噪声和异常值敏感：如果数据集中存在大量噪声或异常值，可能会影响聚类的效果。

使用场景

  • 异常检测：由于DBSCAN对噪声和异常值敏感，因此可以用于异常检测任务。
  • 任意形状的簇：对于需要发现任意形状的簇的应用，如社交网络分析、图像分割等，DBSCAN是一个很好的选择。

  • 数据预处理：在某些机器学习任务中，可以使用DBSCAN对数据进行预处理，以便进一步的分析或分类。

Python示例代码（使用scikit-learn库）: 

      
        from sklearn.cluster import DBSCAN  # 导入DBSCAN聚类算法    
      
      
        from sklearn import datasets  # 导入datasets用于生成样本数据    
      
      
        import matplotlib.pyplot as plt  # 导入绘图库    
      
    
      
        
          # 生成样本数据    
        
      
      
        iris = datasets.load_iris()  # 使用Iris数据集作为示例    
      
      
        X = iris["data"]  # 提取特征矩阵    
      
    

      
        
          # 创建DBSCAN对象并拟合数据    
        
      
      
        dbscan = DBSCAN(eps=0.3, min_samples=5)  # eps是邻域半径，min_samples是形成核心对象的最小点数    
      
      
        labels = dbscan.fit_predict(X)  # 获取每个样本点的聚类标签    
      
    

      
        
          # 可视化结果    
        
      
      
        plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  # 使用viridis色彩映射绘制结果图    
      
      
        plt.show()  # 显示结果图  ```

5、K-Means 聚类模型

模型原理

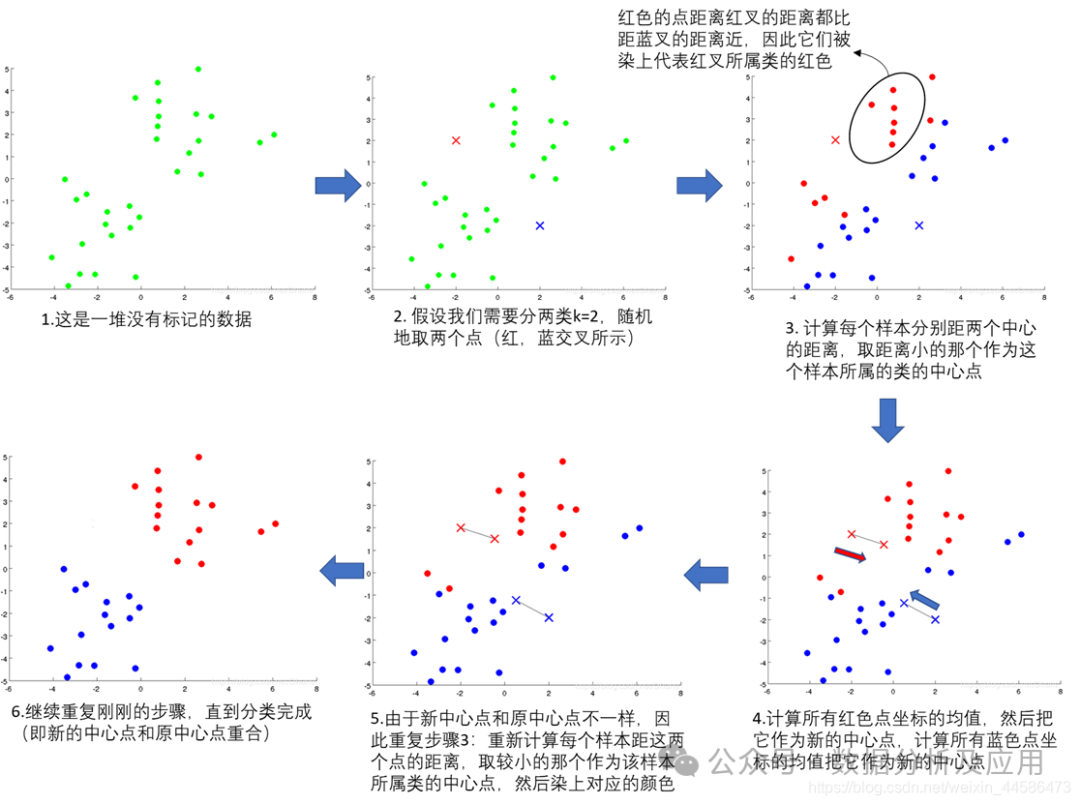
K-Means聚类是一种基于距离的聚类方法，通过最小化每个数据点到其所属簇中心点的距离之和，将数据点划分为K个簇。算法的主要思想是：每个簇有一个中心点，数据点被分配到最近的中心点所在的簇中。通过迭代更新每个簇的中心点，使得所有数据点到其所属簇的中心点的距离之和最小。

313055608d563e5f61fc2f44631ec944.webp

模型训练

  1. 初始化：随机选择K个中心点。
  2. 分配数据点：将每个数据点分配到最近的中心点所在的簇中。
  3. 更新中心点：重新计算每个簇的中心点，即簇中所有数据点的均值。
  4. 重复：重复步骤2和3，直到中心点不再发生显著变化或达到预设的迭代次数。

  5. 输出：返回K个簇的结果。

0a35989aee211d0302196a0dd22929ea.webp

优点

  • 简单易理解：K-Means聚类模型简单直观，易于理解。
  • 可扩展性：对于大规模数据集，K-Means算法具有较好的可扩展性。
  • 无监督学习：K-Means是一种无监督学习方法，适用于未标记的数据集。

  • 对异常值不敏感：由于是基于距离的聚类方法，异常值对聚类结果的影响较小。

缺点

  • 参数敏感：对初始选择的K值和初始中心点敏感，不同的初始参数可能导致不同的聚类结果。
  • 易陷入局部最优解：可能陷入局部最优解，而非全局最优解。
  • 形状限制：只能发现球形簇，对于非球形簇的形状可能无法准确识别。

  • 计算量大：对于高维数据，计算量较大。

使用场景

  • 异常检测：K-Means聚类可以用于异常检测，将异常值识别为与其它数据点距离较远的簇。
  • 市场细分：在市场营销领域，可以使用K-Means聚类将客户划分为不同的细分市场。
  • 图像分割：在图像处理中，可以使用K-Means聚类进行图像分割，将图像划分为多个区域或对象。

  • 特征提取：通过K-Means聚类可以提取数据的内在结构特征，用于分类或预测任务。

Python示例代码（使用scikit-learn库）: 

    
        
          from sklearn.cluster import KMeans  # 导入K-Means聚类算法    
        
        
          from sklearn import datasets  # 导入datasets用于生成样本数据    
        
        
          import matplotlib.pyplot as plt  # 导入绘图库    
        
      
        
          
            # 生成样本数据    
          
        
        
          iris = datasets.load_iris()  # 使用Iris数据集作为示例    
        
        
          X = iris["data"]  # 提取特征矩阵    
        
      
        
          
            # 创建K-Means对象并拟合数据    
          
        
        
          kmeans = KMeans(n_clusters=3)  # 假设有3个簇    
        
        
          labels = kmeans.fit_predict(X)  # 获取每个样本点的聚类标签    
        
      
        
          
            # 可视化结果    
          
        
        
          plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  # 使用viridis色彩映射绘制结果图    
        
        
          plt.show()  # 显示结果图  ```

6、高斯混合模型 

高斯混合模型是一种概率模型，用于表示数据点集合的混合高斯分布。在聚类任务中，高斯混合模型将数据点划分为K个簇，每个簇的数据点都遵循一个高斯分布（正态分布）。

fdb74d90a247ec80847b370084f66620.webp

高斯混合模型的原理基于以下几个假设：

  1. 每个簇的数据点都遵循一个高斯分布：每个簇的分布参数（均值和协方差）由该簇中的数据点估计得出。
  2. 簇之间相互独立：每个簇的高斯分布是独立的，不同簇之间没有依赖关系。

  3. 数据点属于各个簇的概率已知：通过概率模型计算每个数据点属于各个簇的概率。

模型训练

  1. 初始化：随机选择K个中心点，每个中心点初始化为数据集中的一个数据点。
  2. 分配数据点：计算每个数据点到每个中心点的距离，将数据点分配到最近的中心点所在的簇中。
  3. 更新中心点和协方差：重新计算每个簇的中心点和协方差（均值和方差）。
  4. 重新分配数据点：根据新的中心点和协方差，重新分配数据点到各个簇中。
  5. 重复：重复步骤3和4，直到中心点和协方差不再发生显著变化或达到预设的迭代次数。

  6. 输出：返回K个簇的结果，每个簇具有其高斯分布的参数（均值和协方差）。

优点

  • 适用于任意形状的簇：高斯混合模型能够发现任意形状的簇，因为高斯分布可以拟合各种形状的数据分布。
  • 概率模型：高斯混合模型是一个概率模型，能够计算每个数据点属于各个簇的概率，便于后续的分析或应用。

  • 无参数依赖性：高斯混合模型的性能不依赖于特定的参数设置，只需指定簇的数量K。

缺点

  • 对初始参数敏感：初始选择的中心点和初始簇的数量K对最终的聚类结果有一定影响，可能需要多次尝试来获得最佳结果。
  • 计算量大：随着数据集规模的增大，高斯混合模型的计算量也会显著增加。

  • 需要预设簇数量K：需要预先指定簇的数量K，如果K值选择不当，可能导致聚类结果不佳。

使用场景

  • 聚类任务：高斯混合模型广泛应用于各种聚类任务，如图像分割、文本聚类、市场细分等。
  • 异常检测：通过比较数据点到各个簇中心的距离，可以检测异常值。
  • 推荐系统：结合概率模型的特点，可以用于推荐系统中的内容推荐。

  • 生物信息学和化学信息学：在基因表达数据分析、蛋白质分类等生物信息学领域以及化学信息学领域有广泛应用。

Python示例代码（使用scikit-learn库）： 

      
        from sklearn.mixture import GaussianMixture  # 导入高斯混合模型    
      
      
        from sklearn import datasets  # 导入datasets用于生成样本数据    
      
      
        import matplotlib.pyplot as plt  # 导入绘图库  
      
    
      
        
          # 生成样本数据    
        
      
      
        iris = datasets.load_iris()  # 使用Iris数据集作为示例    
      
      
        X = iris["data"]  # 提取特征矩阵    
      
    
      
        
          # 创建高斯混合模型对象并拟合数据    
        
      
      
        gmm = GaussianMixture(n_components=3)  # 假设有3个簇    
      
      
        labels = gmm.fit_predict(X)  # 获取每个样本点的聚类标签   
      
    
      
        
          # 可视化结果    
        
      
      
        plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  # 使用viridis色彩映射绘制结果图    
      
      
        plt.show()  # 显示结果图  ```

三、聚类评估指标

常用评估指标包括外部评价指标和内部评价指标。 外部评价指标是在已知真实标签的情况下评估聚类结果的准确性，而内部评价指标则是在不知道真实标签的情况下评估聚类结果的质量。 外部评价指标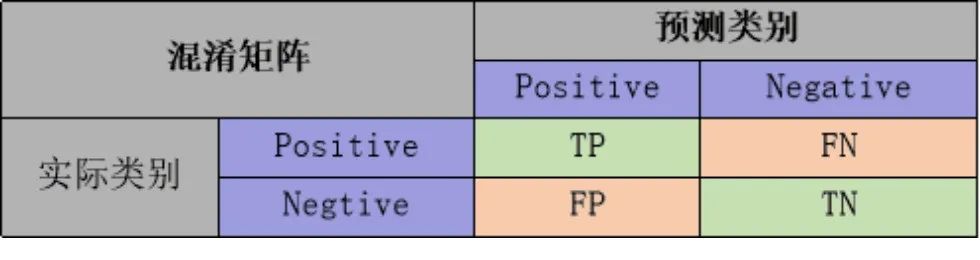： 316eeb5a8e07271305215a72d8281bfa.webp准确率（accuracy）：即所有的预测正确（TP+TN）的占总数（TP+FP+TN+FN）的比例； 查准率P（precision）： 是指分类器预测为Positive的正确样本（TP）的个数占所有预测为Positive样本个数（TP+FP）的比例； 查全率R（recall）： 是指分类器预测为Positive的正确样本（TP）的个数占所有的实际为Positive样本个数（TP+FN）的比例。 F1-score 是查准率P、查全率R的调和平均：

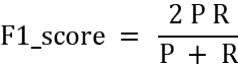
8ace9be94ebb1de6c1ab37428f459a27.webp


调整兰德系数（Adjusted Rand Index, ARI）： 衡量聚类结果与真实标签的匹配程度，取值范围为[-1,1]，值越大表示聚类效果越好。

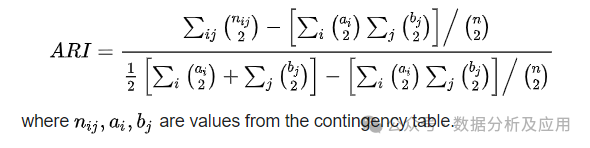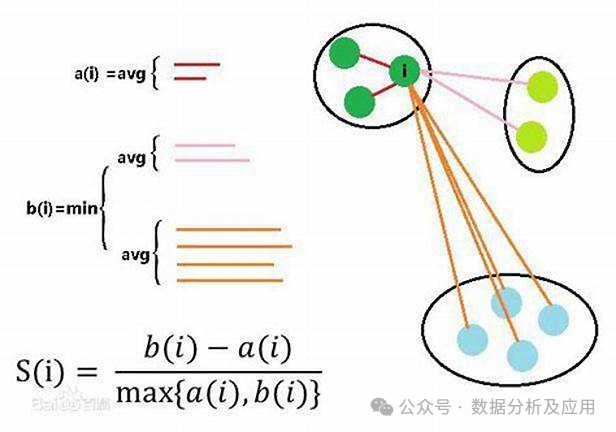
e909ff2d84f58c2727a17fc8cced459a.webp 内部评价指标：
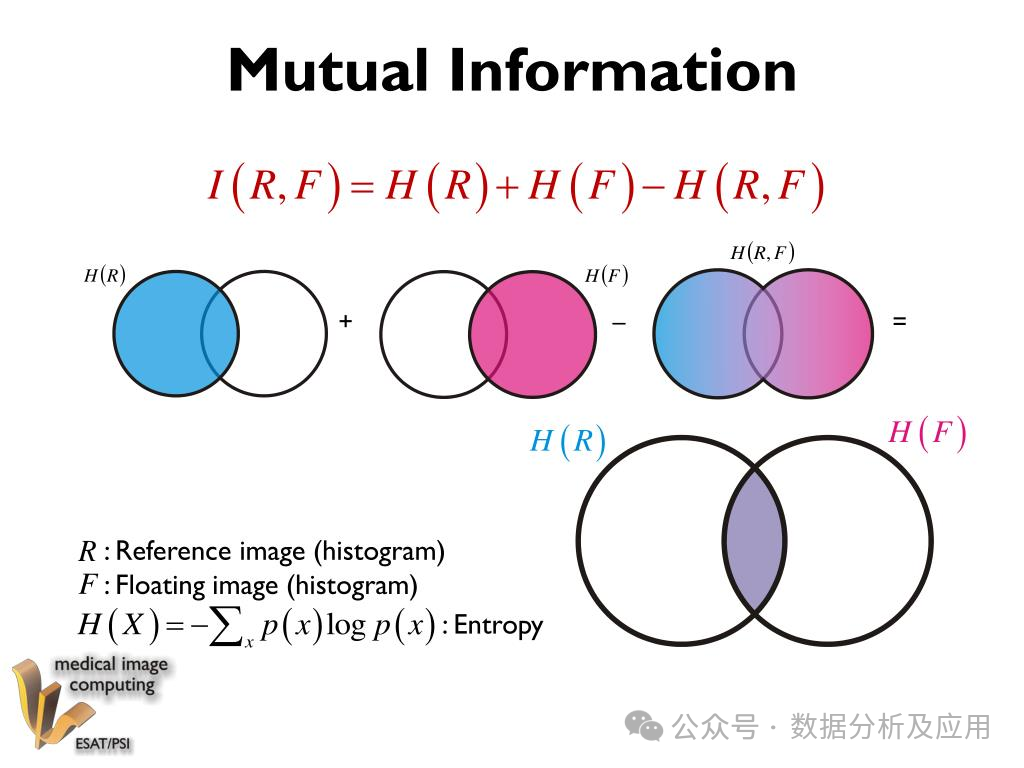
轮廓系数（Silhouette Coefficient）： 通过计算同类样本间的平均距离和不同类样本间的平均距离来评估聚类效果，取值范围为[-1,1]，值越大表示聚类效果越好。 f1345b07d4fdcf32891b106cff08ed82.webp 标准化互信息（Normalized Mutual Information, NMI）： 衡量聚类结果与真实标签的相似性，取值范围为[0,1]，值越大表示聚类效果越好。 互信息（Mutual Information, MI）： 类似于NMI，但不需要对数据进行标准化处理。 8e27114aafc106f150c59fe8d36ab9a9.webp
聚类评估指标对比： 准确率、召回率和F值： 简单易用，但可能不适用于非平衡数据集。
 ARI： 对异常值不敏感，但计算复杂度较高，且对参数设置敏感。 轮廓系数： 考虑了样本间的相对距离，能够更准确地反映聚类效果，但计算复杂度较高。 NMI和MI： 能够准确地评估聚类效果，尤其适用于样本分布不均匀的情况，但计算复杂度较高。 在处理实际问题时，可以尝试多种指标，以便更全面地评估聚类效果。同时， 虽然存在多种量化聚类质量的指标， 但对聚类群的实际评估往往是主观的，并很经常需要结合领域的业务经验。

浏览 6
点赞
评论
收藏
分享

手机扫一扫分享

举报
评论
图片
表情
推荐
常用的聚类算法及聚类算法评价指标
小白学视觉
0
层次聚类算法原理总结
小白学视觉
0
DBSCAN聚类算法原理总结
小白学视觉
0
K8s 超详细总结！
肉眼品世界
0
K8s 超详细总结！
极客挖掘机
0
K8s 超详细总结！
开发者全社区
0
Kubernetes 超详细总结
马哥Linux运维
0
K8s 超详细总结！
程序IT圈
0
4种聚类算法及可视化（Python）
数据派THU
0
超详细｜算法岗学习路线大总结
人工智能与算法学习
0
点赞
评论
收藏
分享

手机扫一扫分享

举报