学习编译原理Time07 ~ 有穷自动机
有穷自动机,是对一类处理系统建立的数学模型,这类系统具有一系列离散的输入输出信息和有穷数目的内部状态,系统只需要根据当前所处的状态和当前面临输入信息就可以决定的后继行为。每当系统处理了当前的输入后,系统的内部状态也将发生改变。

举一个有穷自动机的典型例子
●电梯控制装置
▲输入:顾客的乘梯需求(所要到达的层号)
▲状态:电梯所处的层数+运动方向
电梯控制装置并不需要记住先前全部的服务要求,只需要知道电梯当前所处的状态以及还没有满足的所有服务请求

再来谈谈有穷自动机的模型
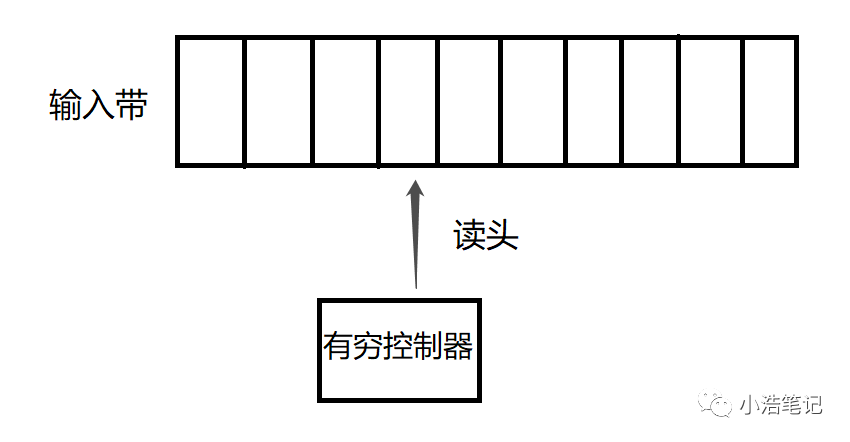
输入带:用来存放输入符号串
读头:从左向右逐个读取输入符号,不能修改(只读),也不能往返移动
有穷控制器:具有有穷个状态数,根据当前的状态和当前输入符号控制转入下一个状态
接下来谈谈有穷自动机的表示——转换图
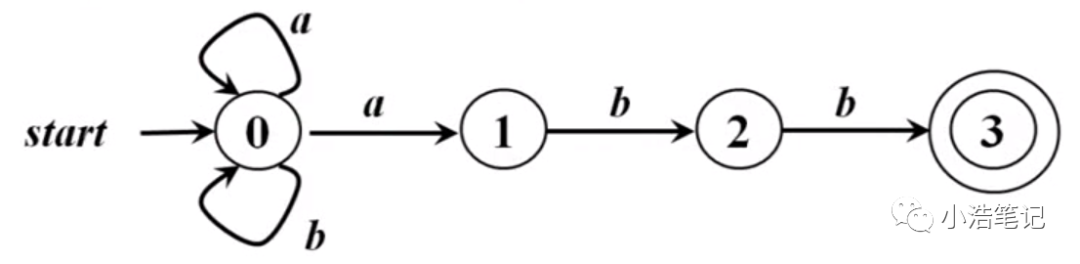
结点:有穷自动机的状态
初始状态(开始状态):只有一个,由start箭头指向
终止状态(接受状态):可以有多个,用双圈表示
带标号的有向边:如果对于输入a,存在一个从状态p到状态q的转换,就在p、q之间画一条有向边,并标记上a
再深入谈谈有穷自动机定义(接受)的语言
给定输入串x,如果存在一个对应于串x的从初始化状态到某个终止状态的转换序列,则称串x被该有穷自动机接收

第一个符号a的时候,状态为0,然后两个字符b,依然是状态0,接着下一个字符a,还是状态0,那么再下一个字符a就进入状态1,接下来,遇到字符b就进入状态2,再遇到字符b就进入状态3,也就是终止状态。可见,这个自动机可接受这个字符串abbaabb。
由一个有穷自动机M接受的所有串构成的集合称为是该有穷自动机定义(接受)的语言,记为L(M)
L(M)=所有以abb结尾的字母表{a,b}上的串的集合

小浩笔记

评论
