DARTS是第一个提出基于松弛连续化的，使用梯度下降进行搜索的神经网络架构搜索(neural architecture search， NAS)算法，将最早矿佬们(说的就是你Google)花成千上万个GPU-hour（即用一块卡跑一小时）的搜索算法降低到了一块卡四天就能跑完。这使得我们这种穷苦的实验室也有了研究NAS这个酷炫方法的可能，不愧是年轻人的第一个NAS模型哈哈哈。

DARTS最大的贡献在于使用了Softmax对本来离散的搜索空间进行了连续化，并用类似于元学习中MAMAL的梯度近似，使得只在一个超网络上就可以完成整个模型的搜索，无需反复训练多个模型。（当然，之后基于演化算法和强化学习的NAS方法也迅速地借鉴了超网络这一特性）。

而实际上，DART还有个更大的贡献就是开源了。不过源代码是基于Pytorch 0.3写的，和主流的1.x版本差别很大，所以需要一段时间进行重新复现。我现在写了1.4版本的分布式并行搜索代码，等后续可视化和保存模型都摸熟了会发实现的教程（在做了在做了）。

除此之外，DARTS虽然想法十分优雅，但我个人觉得其在假设上有不少值得推敲的地方。在略读了CVPR2020里有关NAS的20篇论文后，的确很多工作都是针对我觉得很“有趣”的假设做的233。之后，我也会持续更新CVPR2020中NAS有关的论文，尤其是基于梯度下降方法的。

2.1 概念介绍与符号声明

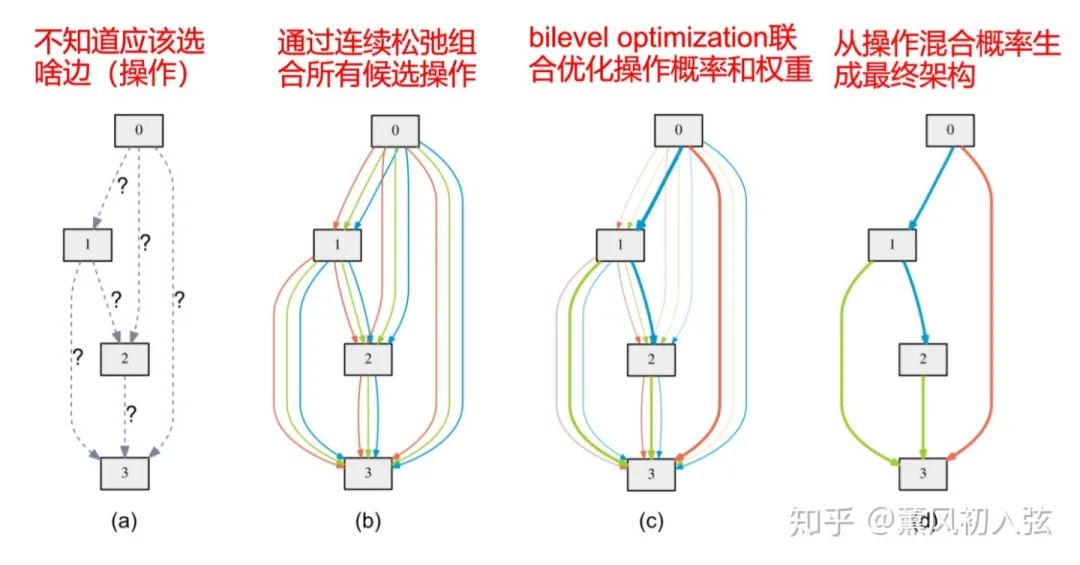
上图为DARTS的算法示意图。首先，这里的搜索空间（对CNN而言）是一个组成模型的Cell，其可以被描述成一个有  个节点的有向无环图。在这个有向无环图中，有节点  和边  ，其中

• 节点 是第  个特征图
• 边是从第  个特征图到第  个特征图之间的变换（如卷积、池化）

此外，所有的边（操作）都是在一个候选操作集  中选取出来的。

2.2 连续松弛化

在传统的方法中，为了在候选操作集  中寻找最好的操作，都是使用强化学习或者演化算法等启发式算法取某个操作，也就是说这种选择是非此即彼的离散操作。

可以看到这里引入了新的符号  ，其含义为：第  个特征图到第  个特征图之间的操作  的权重。这也是我们之后需要搜索的架构参数。

举个例子，如果这个操作的权重  ，那么就可以认为我们完全不需要这个操作。

而为了保证所有节点的输出大致稳定，我们要对每两个节点之间的架构参数（即操作的权重）进行Softmax操作，即  。

可以看到，如果每个操作的权重确定，那么最终的网络架构也随之确定，因此我们后续可以称  为网络架构（的编码）本身。

2.3 两级最优化

这里令训练损失和验证损失分别为  和  。网络中操作的的权重为  ，有 * 上标则说明其为最优的。因此，我们其实希望找到的是一个能在训练集训练好之后（最优权重  )，在验证集上损失最小的架构（  ）。

这里就有个问题，每次我们判断架构好不好的之前，首先他要先在训练集上收敛，即  。而最优的权重本身必然是和架构对应的，架构变化，对应的权重也会跟着变化。

把上面这个过程用数学语言描述，就是以架构  为上级变量，权重  为下级变量的两级最优化问题：

2.4 近似梯度

但是这又有个问题，那就是由二级最优化的定义，每次更新架构参数都理应重新训练模型的权重，但这显然是不可接受的（因为太慢了……）。DARTS算法实际上在验证集上的搜索过程中，权重是不会变的，这就需要某种梯度近似的方法。这里先给出作者提出的（二阶）梯度近似（其中  是权重的学习率）

这种近似在架构于训练集上达到局部极值点（  ）时，  。

也就是说，这种近似实际上是用  （训练集上对权重执行一次梯度下降）来近似最优权重  。

1. 在验证集损失上梯度下降更新架构参数
2. 在训练集损失上梯度下降更新操作权重

李斌：【论文笔记】DARTS公式推导

首先，上面这个近似的梯度涉及了二元复合函数，因此对其求导需要用到链式法则。为了简单可以先将  记为  ，其中：

其中（  ）：

• 
• 
•  （复合函数对第一项的偏微分）
•  （复合函数对第二项的偏微分）

为啥说是具体可求呢，因为在上式第二行的结果中  变成了一个常数，而不是之前一个变量为架构参数  的复合函数！

因此作者提出使用有限差分近似来求解，具体地，设有一小标量  （经验中取  ）。

其中 

现在我们用  来替代  ，则有

之后，用  替代  ， 再把  换成  ，还有把  换成  ，最后把  换成  ，就是有限差分近似的结果啦~

实际上这种有限差分近似只需要对梯度进行两次前向传播，以及对架构进行两次反向传播。其计算复杂度也会从  降至 

最后，如果你觉得这个有限差分近似依然很烦，你w可以直接把第二项扔掉，即只保留  。这种操作等价于假设当前的权重  就是最优权重  ,此时梯度将退化为一阶近似。

2.5 生成最优模型

3.1 "有趣"的假设

1. CNN可以由相同的Cell堆叠得到，RNN可以由相同的Cell递归连接得到
2. 每个Cell有两个输入节点和一个输出节点组成，对于CNN来说输入节点是前两个Cell的输出(the cell outputs of the in the previous two layers)
   
3. 每个Cell的输出实际上是对所有中间节点作reduction操作（比如concatenate）得到的
4. 在验证集上效果最好的模型，在测试集上效果也最好
5. 作者并没有证明这个梯度近似的收敛性，所以直接拿来用了hhh
6. 作者将每个Cell的每个节点之间都取前2个最大权重的操作，（作者的理由是别人都是这么做的）
7. 作者忽略了定义在搜索空间中的0操作（因为作者认为0操作在搜索过程中不会改变运算的结果）
8. 在小模型搜到的Cell在大模型上也会很好用，因此无需重新搜索。
9. Reduction Cell 和 Normal Cell的搜索空间是一样的，且全都是深度可分离卷积，都有池化层。

假设2和6 Follow了谷歌大脑18年CVPR的论文Learning Transferable Architectures for Scalable Image Recognition。不过这篇论文中取的两个输入具体是之前哪两个cell实际上是不固定的，而Darts则固定只取前两个（存疑）

3.2 作者给出的下一步方向

连续体系结构编码和派生离散模型之间存在差异，所以最好让引入类似有退火阈值的01编码。

在搜索工程中学到的共享参数是否可以用于设计一个性能可感知（performance aware）的架构派生机制。

推荐阅读

• 网络搜索之DARTS, GDAS, DenseNAS, P-DARTS, PC-DARTS
  

• 2020 神经网络架构搜索（NAS）最新技术综述
  

• NAS: One-Shot方法总结

添加极市小助手微信（ID : cvmart2），备注：姓名-学校/公司-研究方向-城市（如：小极-北大-目标检测-深圳），即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群：每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~

△长按添加极市小助手

△长按关注极市平台，获取最新CV干货

觉得有用麻烦给个在看啦~