用这种解题方法,我解决了大部分的 leetcode 贪心算法题
“这是本人第40篇原创博文,每周两篇更新,谢谢赏脸阅读文章
今天介绍一种解决常规的贪心策略或者字典排序的题目的通用解题方法。
第一题,leetcode中等难度题目
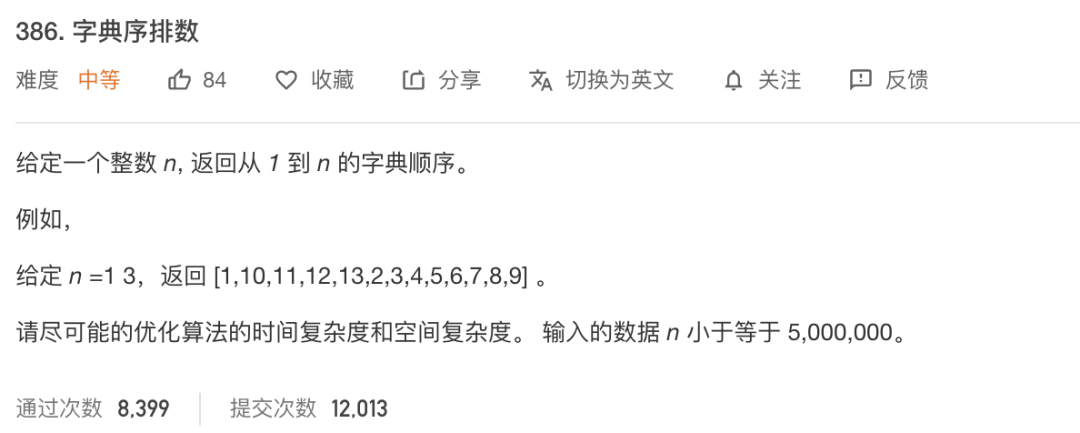
先来一道简单的字典序排列的问题,这个题目我这里不会用最优解来解决这个问题,这个是leetcode的中等难度的题目,最优解还是需要再思考一下的,这道题目作为文章开头只是为了介绍我想要介绍的贪心的解题的一种思路而已,大佬请勿喷!!
看到这个题目,我就是想用暴力的方法解决,以便更好的理解这种解题思路。
先给出我的答案,非常暴力,但是非常好理解。
public List lexicalOrder(int n) {
List list = new ArrayList<>();
for(int i = 1; i <= n; i++){
list.add(i + "");
}
Collections.sort(list,(o1,o2)->{
return o1.compareTo(o2);
});
List iList = new ArrayList<>();
list.stream().forEach((str)->{
iList.add(Integer.parseInt(str));
});
return iList;
}
这个解题方法很简单,用的就是Collections.sort()方法的排序,然后重写一下Comparator类而已,这里用的是lambda表达式,使得代码更加的简洁。
最优解大家可以去leetcode看看哈,自己动手,丰衣足食。
所以,通过这个题目我想给出的信息就是:通常涉及到字符串排序,字典序,数字排序等等的题目,都是可以用这种思路来解决问题的。
不信,我们再看看其他题目。
第二题,leetcode中等难度题目
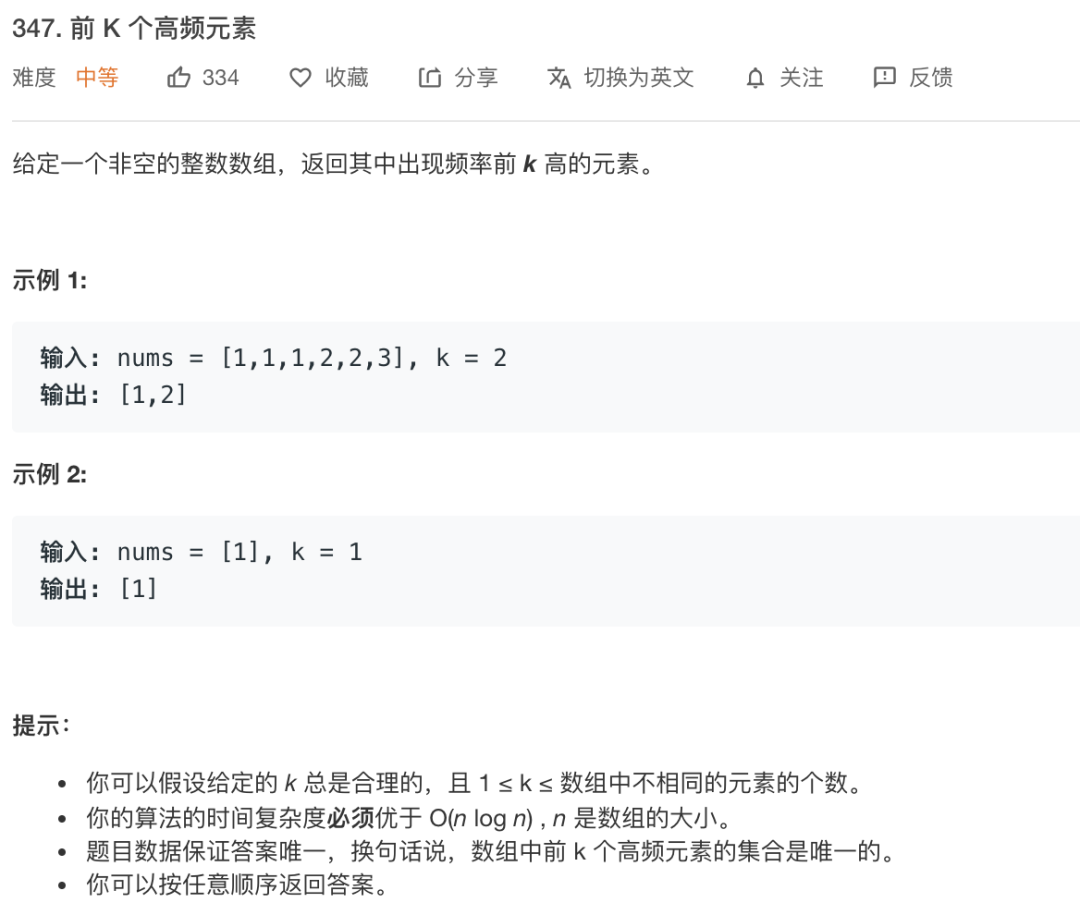
这是一道常见的topk问题,最优解也不是我给出的答案,目的只是为了阐述这种解题方法。
我的解题方法:用优先级队列,维护一个大小为k小顶堆,每次堆的元素到达k时,先弹出堆顶元素,这样就堆总是维持着k个最大值,最终可以的到前k高的元素。
下面看看我的解答(注意:我的答案绝对不是最优解,只是为了阐述这种方法)
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Queue queue = new PriorityQueue<>(k,(o1,o2)->{
return o2.num - o1.num;
});
HashMap map = new HashMap<>();
for(int i = 0; i < nums.length; i++){
map.put(nums[i],map.getOrDefault(nums[i],0) + 1);
}
for(int key : map.keySet()){
queue.offer(new Obj(key,map.get(key)));
}
int[] ans = new int[k];
int i = 0;
while(i < k){
ans[i] = queue.poll().target;
i++;
}
return ans;
}
class Obj {
public int target;
public int num;
public Obj(int target, int num){
this.target = target;
this.num = num;
}
}
}
这种方法没有维护k的最大的堆。
class Solution {
public List topKFrequent(int[] nums, int k) {
HashMap map = new HashMap();
for (int n: nums) {
map.put(n, map.getOrDefault(n, 0) + 1);
}
PriorityQueue heap =
new PriorityQueue((n1, n2) -> map.get(n1) - map.get(n2));
for (int n: map.keySet()) {
heap.add(n);
if (heap.size() > k)
heap.poll();
}
List top_k = new LinkedList();
while (!heap.isEmpty())
top_k.add(heap.poll());
Collections.reverse(top_k);
return top_k;
}
}
这种方法维护k的最大的堆。
对比发现:不管维护k的最大堆还是不维护,核心的思想都是
Queue queue = new PriorityQueue<>(k,(o1,o2)->{
return o2.num - o1.num;
});
和这段代码
PriorityQueue heap =
new PriorityQueue((n1, n2) -> map.get(n1) - map.get(n2));
对比第一题中的
Collections.sort(list,(o1,o2)->{
return o1.compareTo(o2);
});
用的都是内部类:Comparator,然后进行构建符合题意的排序规则。
第三题,更复杂点的

这个题目就更能明白什么是构建符合题意的排序规则。
因为很多题目不止让你根据一个字段进行排序,可能是两个字段进行排序,或者三个字段进行排序,所以就需要进行“构建”。
这个题目的解题思路:先排序再插入
排序规则:按照先H高度降序,K个数升序排序 遍历排序后的数组,根据K插入到K的位置上
核心思想:高个子先站好位,矮个子插入到K位置上,前面肯定有K个高个子,矮个子再插到前面也满足K的要求。
再看看解答
public int[][] reconstructQueue(int[][] people) {
// [7,0], [7,1], [6,1], [5,0], [5,2], [4,4]
// 再一个一个插入过程
// [7,0]
// [7,0], [7,1]
// [7,0], [6,1], [7,1]
// [5,0], [7,0], [6,1], [7,1]
// [5,0], [7,0], [5,2], [6,1], [7,1]
// [5,0], [7,0], [5,2], [6,1], [4,4], [7,1]
Arrays.sort(people, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]);
LinkedList<int[]> list = new LinkedList<>();
for (int[] i : people) {
//在i位置,插入数:i[1]是[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]的第一个数,表示前面有几个比我高的。
list.add(i[1], i);
}
return list.toArray(new int[list.size()][2]);
}
你会发现,核心代码还是跟第一题和第二题一样,只是复杂一点点。
Arrays.sort(people, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]);
这是什么意思呢:o1和o2是一个类似这样[7,0]的一位数组,当第一个数相等时,再比较一维数组的第二个数的大小,不相等,当然先比较第一个数了。
这个就是多个字段比较的例子,是不是还是跟前面的思路是一样的。
总结
最后发现,关于排序的,不管是,数组的排序,数字的排序,字符串的排序,还是优先级队列的排序,我们都是可以用Java的Comparator来解决的。
就说这么多,只是思路,不要死磕最优解!!!
