机器学习基础：11 种特征选择策略总结！-技术圈

来源：DeepHub IMBA，编辑：数据派THU

本文与你分享可应用于特征选择的各种技术的有用指南。

太多的特征会增加模型的复杂性和过拟合，而太少的特征会导致模型的拟合不足。将模型优化为足够复杂以使其性能可推广，但又足够简单易于训练、维护和解释是特征选择的主要工作。

“特征选择”意味着可以保留一些特征并放弃其他一些特征。本文的目的是概述一些特征选择策略：

删除未使用的列
删除具有缺失值的列
不相关的特征
低方差特征
多重共线性
特征系数
p 值
方差膨胀因子 (VIF)
基于特征重要性的特征选择
使用 sci-kit learn 进行自动特征选择
主成分分析 (PCA)

该演示的数据集在 MIT 许可下发布，来自 PyCaret——一个开源的低代码机器学习库。

数据集相当干净，但我做了一些预处理。请注意，我使用此数据集来演示不同的特征选择策略如何工作，而不是构建最终模型，因此模型性能无关紧要。

首先加载数据集：

import pandas as pddata = 'https://raw.githubusercontent.com/pycaret/pycaret/master/datasets/automobile.csv'df = pd.read_csv(data)
df.sample(5)

该数据集包含 202 行和 26 列——每行代表一个汽车实例，每列代表其特征和相应的价格。这些列包括：

df.columns
>> Index(['symboling', 'normalized-losses', 'make', 'fuel-type', 'aspiration', 'num-of-doors', 'body-style', 'drive-wheels', 'engine-location','wheel-base', 'length', 'width', 'height', 'curb-weight', 'engine-type', 'num-of-cylinders', 'engine-size', 'fuel-system', 'bore', 'stroke', 'compression-ratio', 'horsepower', 'peak-rpm', 'city-mpg', 'highway-mpg', 'price'], dtype='object')

现在让我们深入研究特征选择的 11 种策略。

1.删除未使用的列

当然，最简单的策略是你的直觉。虽然是直觉，但有时很有用的，某些列在最终模型中不会以任何形式使用（例如“ID”、“FirstName”、“LastName”等列）。如果您知道某个特定列将不会被使用，请随时将其删除。在我们的数据中，没有一列有这样的问题所以，我在此步骤中不删除任何列。

2.删除具有缺失值的列

缺失值在机器学习中是不可接受的，因此我们会采用不同的策略来清理缺失数据（例如插补）。但是如果列中缺少大量数据，那么完全删除它是非常好的方法。


# total null values per columndf.isnull().sum()
>>symboling             0normalized-losses   35make                 0fuel-type             0aspiration           0num-of-doors         2body-style           0drive-wheels         0engine-location       0wheel-base           0length               0width                 0height               0curb-weight           0engine-type           0num-of-cylinders     0engine-size           0fuel-system           0bore                 0stroke               0compression-ratio     0horsepower           0peak-rpm             0city-mpg             0highway-mpg           0price                 0dtype: int64

3.不相关的特征

无论算法是回归（预测数字）还是分类（预测类别），特征都必须与目标相关。如果一个特征没有表现出相关性，它就是一个主要的消除目标。可以分别测试数值和分类特征的相关性。

数值变量

# correlation between target and features(df.corr().loc['price'].plot(kind='barh', figsize=(4,10)))

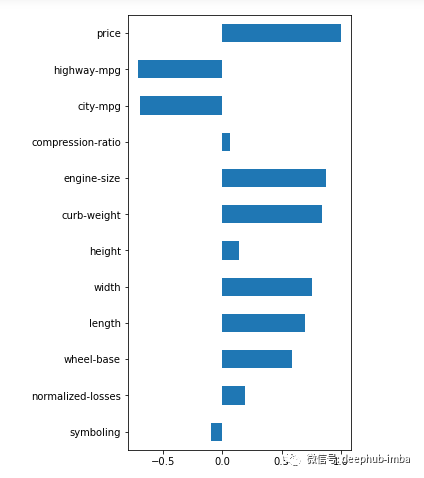
在此示例中，peak-rpm, compression-ratio, stroke, bore, height , symboling 等特征与价格几乎没有相关性，因此我们可以删除它们。

可以手动删除列，但我更喜欢使用相关阈值（在本例中为 0.2）以编程方式进行：


# drop uncorrelated numeric features (threshold <0.2)corr = abs(df.corr().loc['price'])corr = corr[corr<0.2]cols_to_drop = corr.index.to_list()df = df.drop(cols_to_drop, axis=1)

分类变量

可以使用箱线图查找目标和分类特征之间的相关性：

import seaborn as sns
sns.boxplot(y = 'price', x = 'fuel-type', data=df)

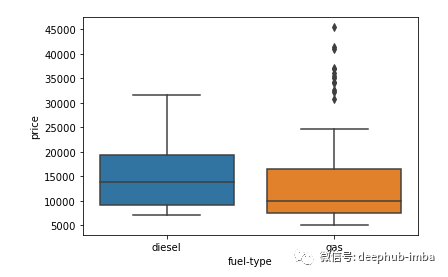
柴油车的中位价高于汽油车。这意味着这个分类变量可以解释汽车价格，所以应放弃它。可以像这样单独检查每个分类列。

4.低方差特征

检查一下我们的特征的差异：

import numpy as np
# variance of numeric features(df.select_dtypes(include=np.number).var().astype('str'))

这里的“bore”具有极低的方差，虽然这是删除的候选者。在这个特殊的例子中，我不愿意删除它，因为它的值在2.54和3.94之间，因此方差很低：

df['bore'].describe()

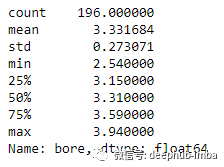
5.多重共线性

当任何两个特征之间存在相关性时，就会出现多重共线性。在机器学习中，期望每个特征都应该独立于其他特征，即它们之间没有共线性。高马力车辆往往具有高发动机尺寸。所以你可能想消除其中一个，让另一个决定目标变量——价格。

我们可以分别测试数字和分类特征的多重共线性：

数值变量

Heatmap 是检查和寻找相关特征的最简单方法。

import matplotlib.pyplot as plt
sns.set(rc={'figure.figsize':(16,10)})sns.heatmap(df.corr(),          annot=True,          linewidths=.5,          center=0,          cbar=False,          cmap="PiYG")plt.show()

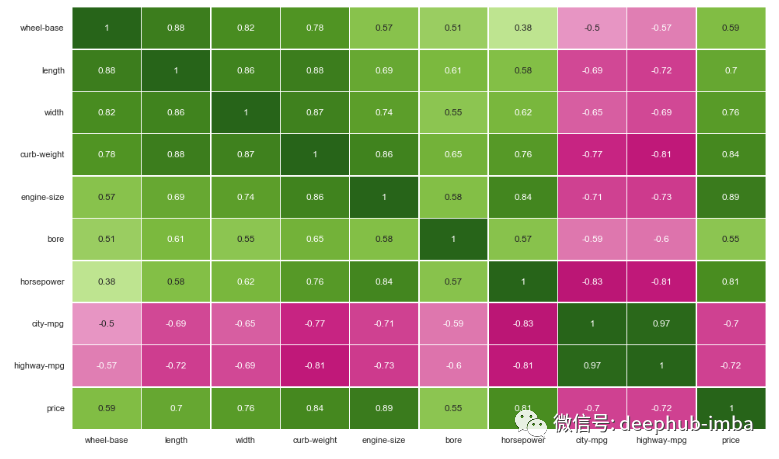
大多数特征在某种程度上相互关联，但有些特征具有非常高的相关性，例如长度与轴距以及发动机尺寸与马力。

可以根据相关阈值手动或以编程方式删除这些功能。我将手动删除具有 0.80 共线性阈值的特征。

# drop correlated featuresdf = df.drop(['length', 'width', 'curb-weight', 'engine-size', 'city-mpg'], axis=1)

还可以使用称为方差膨胀因子 (VIF) 的方法来确定多重共线性并根据高 VIF 值删除特征。我稍后会展示这个例子。

分类变量

与数值特征类似，也可以检查分类变量之间的共线性。诸如独立性卡方检验之类的统计检验非常适合它。

让我们检查一下数据集中的两个分类列——燃料类型和车身风格——是独立的还是相关的。

df_cat = df[['fuel-type', 'body-style']]df_cat.sample(5)

然后我们将在每一列中创建一个类别的交叉表/列联表。

crosstab = pd.crosstab(df_cat['fuel-type'], df_cat['body-style'])crosstab

最后，我们将在交叉表上运行卡方检验，这将告诉我们这两个特征是否独立。

from scipy.stats import chi2_contingency
chi2_contingency(crosstab)

输出依次是卡方值、p 值、自由度和预期频率数组。

p 值 <0.05，因此我们可以拒绝特征之间没有关联的原假设，即两个特征之间存在统计上显着的关系。

由于这两个特征之间存在关联，我们可以选择删除其中一个。

到目前为止，我已经展示了在实现模型之前应用的特征选择策略。这些策略在第一轮特征选择以建立初始模型时很有用。但是一旦构建了模型，就可以获得有关模型性能中每个特征的适应度的更多信息。根据这些新信息，可以进一步确定要保留哪些功能。

下面我们使用最简单的线性模型展示其中的一些方法。


# drop columns with missing valuesdf = df.dropna()from sklearn.model_selection import train_test_split# get dummies for categorical featuresdf = pd.get_dummies(df, drop_first=True)# X featuresX = df.drop('price', axis=1)# y targety = df['price']# split data into training and testing setX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
from sklearn.linear_model import LinearRegression# scalingfrom sklearn.preprocessing import StandardScalerscaler = StandardScaler()X_train = scaler.fit_transform(X_train)X_test = scaler.fit_transform(X_test)# convert back to dataframeX_train = pd.DataFrame(X_train, columns = X.columns.to_list())X_test = pd.DataFrame(X_test, columns = X.columns.to_list())# instantiate modelmodel = LinearRegression()# fitmodel.fit(X_train, y_train)

现在我们已经拟合了模型，让我们进行另一轮特征选择。

6.特征系数

如果正在运行回归任务，则特征适应度的一个关键指标是回归系数（所谓的 beta 系数），它显示了模型中特征的相对贡献。有了这些信息，可以删除贡献很小或没有贡献的功能。

# feature coefficientscoeffs = model.coef_
# visualizing coefficientsindex = X_train.columns.tolist()
(pd.DataFrame(coeffs, index = index, columns = ['coeff']).sort_values(by = 'coeff').plot(kind='barh', figsize=(4,10)))

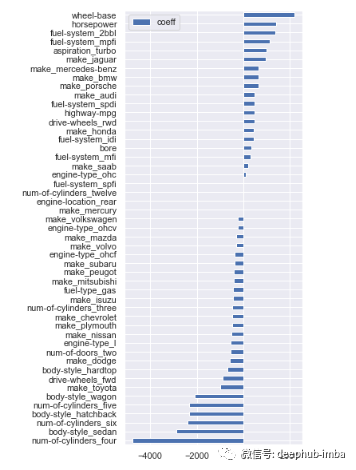
某些特征beta 系数很小，对汽车价格的预测贡献不大。可以过滤掉这些特征：


# filter variables near zero coefficient valuetemp = pd.DataFrame(coeffs, index = index, columns = ['coeff']).sort_values(by = 'coeff')temp = temp[(temp['coeff']>1) | (temp['coeff']< -1)]
# drop those featurescols_coeff = temp.index.to_list()X_train = X_train[cols_coeff]X_test = X_test[cols_coeff]

7.p 值

在回归中，p 值告诉我们预测变量和目标之间的关系是否具有统计显著性。statsmodels 库提供了带有特征系数和相关 p 值的回归输出的函数。

如果某些特征不显著，可以将它们一个一个移除，然后每次重新运行模型，直到找到一组具有显着 p 值的特征，并通过更高的调整 R2 提高性能。

import statsmodels.api as smols = sm.OLS(y, X).fit()print(ols.summary())

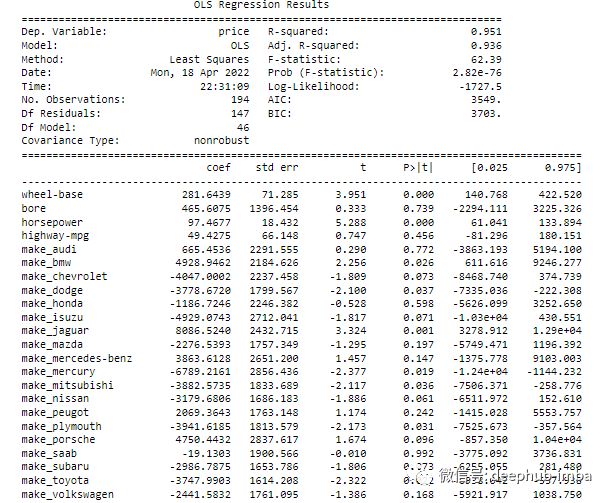
8.方差膨胀因子 (VIF)

方差膨胀因子 (VIF) 是衡量多重共线性的另一种方法。它被测量为整体模型方差与每个独立特征的方差的比率。一个特征的高 VIF 表明它与一个或多个其他特征相关。根据经验：

VIF = 1 表示无相关性
VIF = 1-5 中等相关性
VIF >5 高相关

VIF 是一种消除多重共线性特征的有用技术。对于我们的演示，将所有 VIF 高于10的删除。

from statsmodels.stats.outliers_influence import variance_inflation_factor
# calculate VIFvif = pd.Series([variance_inflation_factor(X.values, i) for i in range(X.shape[1])], index=X.columns)
# display VIFs in a tableindex = X_train.columns.tolist()vif_df = pd.DataFrame(vif, index = index, columns = ['vif']).sort_values(by = 'vif', ascending=False)vif_df[vif_df['vif']<10]

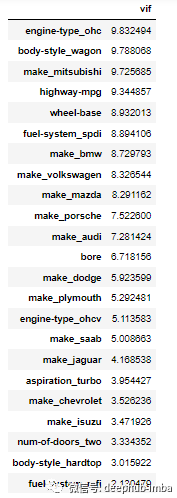
9.基于特征重要性选择

决策树/随机森林使用一个特征来分割数据，该特征最大程度地减少了杂质(以基尼系数杂质或信息增益衡量)。找到最佳特征是算法如何在分类任务中工作的关键部分。我们可以通过 feature_importances_ 属性访问最好的特征。

让我们在我们的数据集上实现一个随机森林模型并过滤一些特征。


from sklearn.ensemble import RandomForestClassifier
# instantiate modelmodel = RandomForestClassifier(n_estimators=200, random_state=0)# fit modelmodel.fit(X,y)

现在让我们看看特征重要性：

# feature importanceimportances = model.feature_importances_
# visualizationcols = X.columns(pd.DataFrame(importances, cols, columns = ['importance']).sort_values(by='importance', ascending=True).plot(kind='barh', figsize=(4,10)))

上面的输出显示了每个特征在减少每个节点/拆分处的重要性。

由于随机森林分类器有很多估计量（例如上面例子中的 200 棵决策树），可以用置信区间计算相对重要性的估计值。

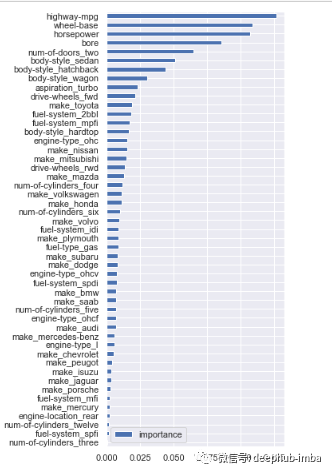
# calculate standard deviation of feature importancesstd = np.std([i.feature_importances_ for i in model.estimators_], axis=0)
# visualizationfeat_with_importance = pd.Series(importances, X.columns)fig, ax = plt.subplots(figsize=(12,5))feat_with_importance.plot.bar(yerr=std, ax=ax)ax.set_title("Feature importances")ax.set_ylabel("Mean decrease in impurity")

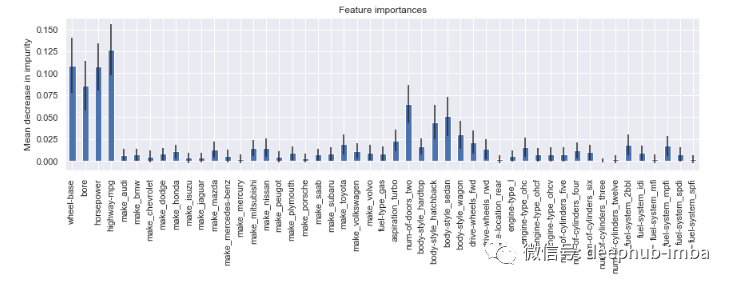
现在我们知道了每个特征的重要性，可以手动（或以编程方式）确定保留哪些特征以及删除哪些特征。

10.使用 Scikit Learn 自动选择特征

sklearn 库中有一个完整的模块，只需几行代码即可处理特征选择。

sklearn 中有许多自动化流程，但这里我只展示一些：

# import modulesfrom sklearn.feature_selection import (SelectKBest, chi2, SelectPercentile, SelectFromModel, SequentialFeatureSelector, SequentialFeatureSelector)

基于卡方的技术

基于卡方的技术根据一些预定义的分数选择特定数量的用户定义特征 (k)。这些分数是通过计算 X（独立）和 y（因）变量之间的卡方统计量来确定的。在 sklearn 中，需要做的就是确定要保留多少特征。如果想保留 10 个功能，实现将如下所示：


# select K best featuresX_best = SelectKBest(chi2, k=10).fit_transform(X,y)
# number of best featuresX_best.shape[1]
>> 10

如果有大量特征，可以指定要保留的特征百分比。假设我们想要保留 75% 的特征并丢弃剩余的 25%：


# keep 75% top featuresX_top = SelectPercentile(chi2, percentile = 75).fit_transform(X,y)
# number of best featuresX_top.shape[1]
>> 36

正则化

正则化减少了过拟合。如果你有太多的特征，正则化控制它们的效果，或者通过缩小特征系数（称为 L2 正则化）或将一些特征系数设置为零（称为 L1 正则化）。

一些模型具有内置的 L1/L2 正则化作为超参数来惩罚特征。可以使用转换器 SelectFromModel 消除这些功能。

让我们实现一个带有惩罚 = 'l1' 的 LinearSVC 算法。然后使用 SelectFromModel 删除一些功能。


# implement algorithmfrom sklearn.svm import LinearSVCmodel = LinearSVC(penalty= 'l1', C = 0.002, dual=False)model.fit(X,y)# select features using the meta transformerselector = SelectFromModel(estimator = model, prefit=True)
X_new = selector.transform(X)X_new.shape[1]
>> 2
# names of selected featuresfeature_names = np.array(X.columns)feature_names[selector.get_support()]
>> array(['wheel-base', 'horsepower'], dtype=object)

序贯法

序贯法是一种经典的统计技术。在这种情况下一次添加/删除一个功能并检查模型性能，直到它针对需求进行优化。

序贯法有两种变体。前向选择技术从 0 特征开始，然后添加一个最大程度地减少错误的特征；然后添加另一个特征，依此类推。

向后选择在相反的方向上起作用。模型从包含的所有特征开始并计算误差；然后它消除了一个可以进一步减少误差的特征。重复该过程，直到保留所需数量的特征。

# instantiate modelmodel = RandomForestClassifier(n_estimators=100, random_state=0)
# select featuresselector = SequentialFeatureSelector(estimator=model, n_features_to_select=10, direction='backward', cv=2)selector.fit_transform(X,y)
# check names of features selectedfeature_names = np.array(X.columns)feature_names[selector.get_support()]
>> array(['bore', 'make_mitsubishi', 'make_nissan', 'make_saab',      'aspiration_turbo', 'num-of-doors_two', 'body style_hatchback', 'engine-type_ohc', 'num-of-cylinders_twelve', 'fuel-system_spdi'], dtype=object)

11.主成分分析 (PCA)

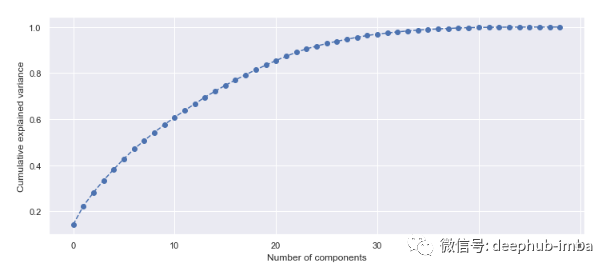
PCA的主要目的是降低高维特征空间的维数。原始特征被重新投影到新的维度（即主成分）。最终目标是找到最能解释数据方差的特征数量。

# import PCA modulefrom sklearn.decomposition import PCA# scaling dataX_scaled = scaler.fit_transform(X)# fit PCA to datapca = PCA()pca.fit(X_scaled)evr = pca.explained_variance_ratio_
# visualizing the variance explained by each principal componentsplt.figure(figsize=(12, 5))plt.plot(range(0, len(evr)), evr.cumsum(), marker="o", linestyle="--")plt.xlabel("Number of components")plt.ylabel("Cumulative explained variance")

20 个主成分解释了超过 80% 的方差，因此可以将模型拟合到这 20 个成分（特征）。可以预先确定方差阈值并选择所需的主成分数量。

总结

这是对可应用于特征选择的各种技术的有用指南。在拟合模型之前应用了一些技术，例如删除具有缺失值的列、不相关的列、具有多重共线性的列以及使用 PCA 进行降维，而在基本模型实现之后应用其他技术，例如特征系数、p 值、 VIF 等。虽然不会在一个项目中完全使用所有策略，这些策略都是我们进行测试的方向。

本文代码：https://github.com/mabalam/feature_selection

作者：Mahbubul Alam 编辑：黄继彦校对：林亦霖