【Python数据挖掘实战案例】K-Means广告效果聚类分析
本案例的业务场景:
假如你们公司投放广告的渠道很多,每个渠道的客户性质也可能不同,比如在优酷视频投广告和今日头条投放广告,效果可能会有差异。现在需要对广告效果分析实现有针对性的广告效果测量和优化工作。
本案例,通过各类广告渠道90天内额日均UV,平均注册率、平均搜索率、访问深度、平均停留时长、订单转化率、投放时间、素材类型、广告类型、合作方式、广告尺寸和广告卖点等特征,将渠道分类,找出每类渠道的重点特征,为加下来的业务讨论和数据分析提供支持。



目 录
1、应用技术介绍
2、数据介绍
3、导入库,加载数据
4、数据审查
5、数据处理
6、建立模型
7、聚类结果特征分析与展示
8、数据结论
应用技术介绍
Law
01、数据预处理
a、数据标准化
数据无量纲化,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或者量级的指标能够进行和加权. 比如身高与体重,房子数量与收入等。
b、独热编码OneHotEncoder
对于字符串类别类型的变量,不能直接带入模型,需要转化为数值型。

02、K-Means聚类算法
聚类算法:属于无监督机器学习算法,通过计算样本项之间的相似度(也称为样本间的距离),按照数据内部存在的数据特征将数据集划分为多个不同的类别,使类别内的数据比较相似,类别之间的数据相似度比较小。
闵可夫斯基距离(Minkowski):
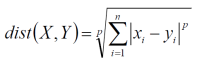
当p为1的时候是曼哈顿距离(Manhattan)
当p为2的时候是欧式距离(Euclidean)
当p为无穷大的时候是切比雪夫距离(Chebyshev)
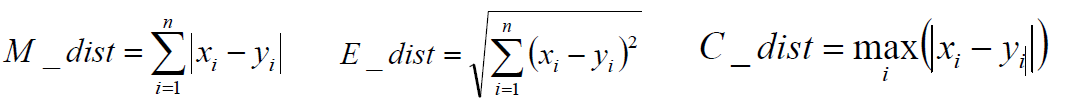
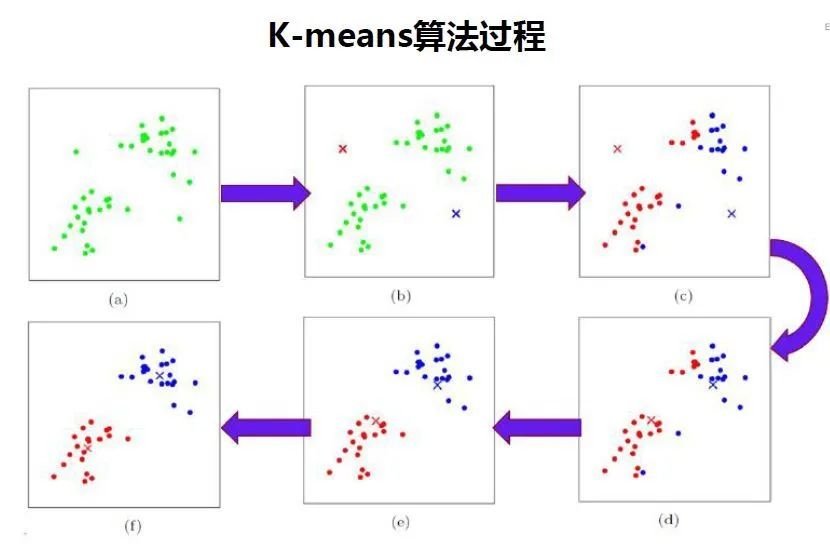
算法思想(步骤):
a、选择初始化的k个类别中心a1,a2,...ak;
b、计算每个样本Xi到类别中心aj的距离,设定最近的类别j
c、将每个类别的中心点aj,替换为隶属该类别的所有样本的均值,作为新的质心。
d、重复上面两步操作,直到达到某个中止条件
中止条件为:组内最小平方误差MSE最小,或者达到迭代次数,或者簇中心点不再变化。
之前文章有介绍(点击下方链接查看):

聚类评估——轮廓系数
如何基于最优的数据尺度确定K-Means算法中的K值?
轮廓系数的思想:
最佳的聚类类别划分从数据特征上看,类内距离最小化且类别间距离最大化,直观的理解就是“物以类聚”:同类的“聚集”“抱团”,不同类的离得远。轮廓系数通过枚举每个K计算平均轮廓系数得到最佳值。
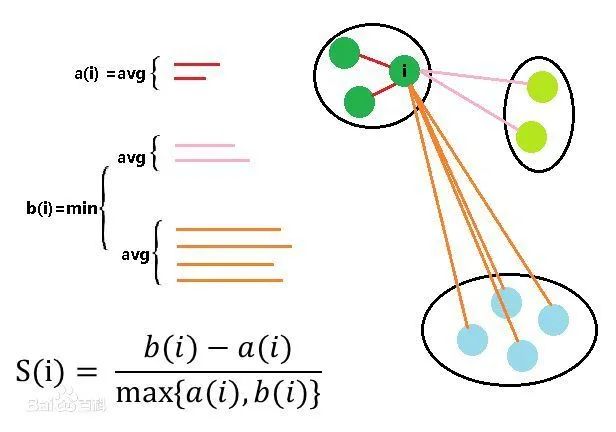
a(i) :i向量到同一簇内其他点不相似程度的平均值
b(i) :i向量到其他簇的平均不相似程度的最小值
轮廓系数的值是介于 [-1,1] ,越趋近于1代表内聚度和分离度都相对较优。
将所有点的轮廓系数求平均,就是该聚类结果总的轮廓系数。
数据介绍
Law
01 数据维度概况
除了渠道唯一标识,共12个维度,889行,有缺失值,有异常值。
02 数据13个维度介绍
'390*270'
导入库,加载数据
Law
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler,OneHotEncoder
from sklearn.metrics import silhouette_score # 导入轮廓系数指标
from sklearn.cluster import KMeans # KMeans模块
%matplotlib inline
## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
以上是加载库的国际惯例,OneHotEncoder是独热编码,如果一个类别特征有n个类别,将该变量按照类别分裂成N维新变量,包含则标记为1,否则为0,用N维特征表示原来的特征。
读取数据:
raw_data = pd.read_table('ad_performance.txt', delimiter='\t')
raw_data.head()
渠道代号 日均UV 平均注册率 平均搜索量 访问深度 平均停留时间 订单转化率 投放总时间 素材类型 广告类型 合作方式 广告尺寸 广告卖点
0 A203 3.69 0.0071 0.0214 2.3071 419.77 0.0258 20 jpg banner roi 140*40 打折
1 A387 178.70 0.0040 0.0324 2.0489 157.94 0.0030 19 jpg banner cpc 140*40 满减
2 A388 91.77 0.0022 0.0530 1.8771 357.93 0.0026 4 jpg banner cpc 140*40 满减
3 A389 1.09 0.0074 0.3382 4.2426 364.07 0.0153 10 jpg banner cpc 140*40 满减
4 A390 3.37 0.0028 0.1740 2.1934 313.34 0.0007 30 jpg banner cpc 140*40 满减
渠道代号是唯一标识,日均UV到投放总时间是数值型(float和int)变量,后面是字符型变量。
数据审查
Law
# 查看基本状态
print('{:*^60}'.format('数据前两行:'))
print(raw_data.head(2)) # 打印输出前2条数据
print('{:*^60}'.format('数据类型:'))
print(pd.DataFrame(raw_data.dtypes).T) # 打印数据类型分布
print('{:*^60}'.format('数据统计描述:'))
print(raw_data.describe().round(2).T) # 打印原始数据基本描述性信息
***************************数据前两行:***************************
渠道代号 日均UV 平均注册率 平均搜索量 访问深度 平均停留时间 订单转化率 投放总时间 素材类型 广告类型 \
0 A203 3.69 0.0071 0.0214 2.3071 419.77 0.0258 20 jpg banner
1 A387 178.70 0.0040 0.0324 2.0489 157.94 0.0030 19 jpg banner
合作方式 广告尺寸 广告卖点
0 roi 140*40 打折
1 cpc 140*40 满减
***************************数据类型:****************************
渠道代号 日均UV 平均注册率 平均搜索量 访问深度 平均停留时间 订单转化率 投放总时间 \
0 object float64 float64 float64 float64 float64 float64 int64
素材类型 广告类型 合作方式 广告尺寸 广告卖点
0 object object object object object
**************************数据统计描述:***************************
count mean std min 25% 50% 75% max
日均UV 889.0 540.85 1634.41 0.06 6.18 114.18 466.87 25294.77
平均注册率 889.0 0.00 0.00 0.00 0.00 0.00 0.00 0.04
平均搜索量 889.0 0.03 0.11 0.00 0.00 0.00 0.01 1.04
访问深度 889.0 2.17 3.80 1.00 1.39 1.79 2.22 98.98
平均停留时间 887.0 262.67 224.36 1.64 126.02 236.55 357.98 4450.83
订单转化率 889.0 0.00 0.01 0.00 0.00 0.00 0.00 0.22
投放总时间 889.0 16.05 8.51 1.00 9.00 16.00 24.00 30.00
上面代码,分别展示前两条数据、所有特征的数据类型、以及数值型特征的五值分布
查看缺失值情况:
# 缺失值审查
na_cols = raw_data.isnull().any(axis=0) # 查看每一列是否具有缺失值
print('{:*^60}'.format('含有缺失值的列:'))
print(na_cols[na_cols==True]) # 查看具有缺失值的列
print('总共有多少数据缺失: {0}'.format(raw_data.isnull().any(axis=1).sum())) # 查看具有缺失值的行总记录数
**************************含有缺失值的列:**************************
平均停留时间 True
dtype: bool
总共有多少数据缺失: 2
# 也可以用下面的代码查看
raw_data.isnull().sum().sort_values(ascending=False)
变量之间的相关性分析:
# 相关性分析
print('{:*^60}'.format('Correlation analysis:'))
print(raw_data.corr().round(2).T) # 打印原始数据相关性信息*******************Correlation analysis:********************
日均UV 平均注册率 平均搜索量 访问深度 平均停留时间 订单转化率 投放总时间
日均UV 1.00 -0.05 -0.07 -0.02 0.04 -0.05 -0.04
平均注册率 -0.05 1.00 0.24 0.11 0.22 0.32 -0.01
平均搜索量 -0.07 0.24 1.00 0.06 0.17 0.13 -0.03
访问深度 -0.02 0.11 0.06 1.00 0.72 0.16 0.06
平均停留时间 0.04 0.22 0.17 0.72 1.00 0.25 0.05
订单转化率 -0.05 0.32 0.13 0.16 0.25 1.00 -0.00
投放总时间 -0.04 -0.01 -0.03 0.06 0.05 -0.00 1.00
前面有有写过,皮尔逊相关的文章,可以用热力图形象展示(放个链接方便回看):
# 相关性可视化展示
import seaborn as sns
corr=raw_data.corr().round(2)
sns.heatmap(corr,cmap="Reds",annot=True)
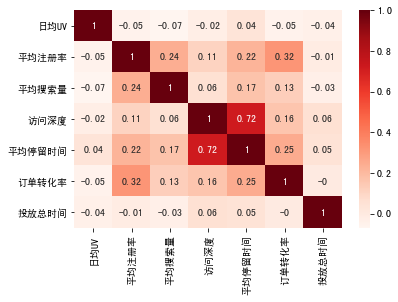
可以看到,“访问深度”和“平均停留时间”相关性比较高,相关性高说明两个变量在建立模型的时候,作用是一样或者效果是一样的,可以考虑组合或者删除其一。
数据处理
Law
数据了解的差不多了,我们开始时处理数据,把常规数据通过清洗、转换、规约、聚合、抽样等方式变成机器学习可以识别或者提升准确度的数据。
# 1 删除平均平均停留时间列
raw_data2 = raw_data.drop(['平均停留时间'], axis=1)
类别变量的独热编码:
# 类别变量取值
cols=["素材类型","广告类型","合作方式","广告尺寸","广告卖点"]
for x in cols:
data=raw_data2[x].unique()
print("变量【{0}】的取值有:\n{1}".format(x,data))
print("-·"*20)
变量【素材类型】的取值有:
['jpg' 'swf' 'gif' 'sp']
-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·
变量【广告类型】的取值有:
['banner' 'tips' '不确定' '横幅' '暂停']
-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·
变量【合作方式】的取值有:
['roi' 'cpc' 'cpm' 'cpd']
-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·
变量【广告尺寸】的取值有:
['140*40' '308*388' '450*300' '600*90' '480*360' '960*126' '900*120'
'390*270']
-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·
变量【广告卖点】的取值有:
['打折' '满减' '满赠' '秒杀' '直降' '满返']
-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·# 字符串分类独热编码处理
cols = ['素材类型','广告类型','合作方式','广告尺寸','广告卖点']
model_ohe = OneHotEncoder(sparse=False) # 建立OneHotEncode对象
ohe_matrix = model_ohe.fit_transform(raw_data2[cols]) # 直接转换
print(ohe_matrix[:2])
out:
[[0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.
0. 0. 0.]
[0. 1. 0. 0. 1. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.
0. 0. 0.]]
# 用pandas的方法
ohe_matrix1=pd.get_dummies(raw_data2[cols])
ohe_matrix1.head(5)
结果如下:
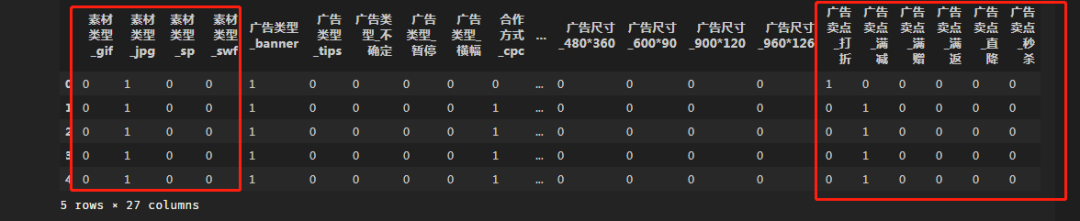
数据标准化:
数据标准化的意义开篇技术介绍有聊过,统一量纲。
# 数据标准化
sacle_matrix = raw_data2.iloc[:, 1:7] # 获得要转换的矩阵
model_scaler = MinMaxScaler() # 建立MinMaxScaler模型对象
data_scaled = model_scaler.fit_transform(sacle_matrix) # MinMaxScaler标准化处理
print(data_scaled.round(2))
[[0. 0.18 0.02 0.01 0.12 0.66]
[0.01 0.1 0.03 0.01 0.01 0.62]
[0. 0.06 0.05 0.01 0.01 0.1 ]
...
[0.01 0.01 0. 0. 0. 0.72]
[0.05 0. 0. 0. 0. 0.31]
[0. 0. 0. 0.53 0. 0.62]]
数据处理完,我们将独热编码的数据和标准化转化后的数据合并:
# 合并所有维度
X = np.hstack((data_scaled, ohe_matrix))数据处理完,就可以带入模型进行训练了。
建立模型
Law
# 通过平均轮廓系数检验得到最佳KMeans聚类模型
score_list = list() # 用来存储每个K下模型的平局轮廓系数
silhouette_int = -1 # 初始化的平均轮廓系数阀值
for n_clusters in range(2, 8): # 遍历从2到5几个有限组
model_kmeans = KMeans(n_clusters=n_clusters) # 建立聚类模型对象
labels_tmp = model_kmeans.fit_predict(X) # 训练聚类模型
silhouette_tmp = silhouette_score(X, labels_tmp) # 得到每个K下的平均轮廓系数
if silhouette_tmp > silhouette_int: # 如果平均轮廓系数更高
best_k = n_clusters # 保存K将最好的K存储下来
silhouette_int = silhouette_tmp # 保存平均轮廓得分
best_kmeans = model_kmeans # 保存模型实例对象
cluster_labels_k = labels_tmp # 保存聚类标签
score_list.append([n_clusters, silhouette_tmp]) # 将每次K及其得分追加到列表
print('{:*^60}'.format('K值对应的轮廓系数:'))
print(np.array(score_list)) # 打印输出所有K下的详细得分
print('最优的K值是:{0} \n对应的轮廓系数是:{1}'.format(best_k, silhouette_int))
*************************K值对应的轮廓系数:*************************
[[2. 0.38655493]
[3. 0.45864451]
[4. 0.50209812]
[5. 0.4800359 ]
[6. 0.47761127]
[7. 0.4935842 ]]
最优的K值是:4
对应的轮廓系数是: 0.5020981194788053
轮廓系数确定最佳的K值,确定数据分为几类较为合理,开篇技术介绍有轮廓系数的介绍了,聚类效果的评价,之前文章有介绍过聚类数和簇内均方误差绘图出现拐点的时候可以确定为几类。
总体思想(评价指标)还是怎么聚才能使得簇内距离足够小,簇与簇之间平均距离足够大来评判。
当然,有兴趣的同学,可以查资料总结一下聚类的评价指标,怎么确定K值,K-Means有什么优缺点,怎么提升?··· ···
后续文章也可能会专门出个这方面的专题。
聚类结果特征分析与展示
Law
通过上面模型,我们其实给每个观测(样本)打了个标签clusters,即他属于4类中的哪一类:
# 将原始数据与聚类标签整合
cluster_labels = pd.DataFrame(cluster_labels_k, columns=['clusters']) # 获得训练集下的标签信息
merge_data = pd.concat((raw_data2, cluster_labels), axis=1) # 将原始处理过的数据跟聚类标签整合
merge_data.head()
渠道代号 日均UV 平均注册率 平均搜索量 访问深度 订单转化率 投放总时间 素材类型 广告类型 合作方式 广告尺寸 广告卖点 clusters
0 A203 3.69 0.0071 0.0214 2.3071 0.0258 20 jpg banner roi 140*40 打折 0
1 A387 178.70 0.0040 0.0324 2.0489 0.0030 19 jpg banner cpc 140*40 满减 0
2 A388 91.77 0.0022 0.0530 1.8771 0.0026 4 jpg banner cpc 140*40 满减 0
3 A389 1.09 0.0074 0.3382 4.2426 0.0153 10 jpg banner cpc 140*40 满减 0
4 A390 3.37 0.0028 0.1740 2.1934 0.0007 30 jpg banner cpc 140*40 满减 0
然后看看,每个类别下的样本数量和占比情况:
# 计算每个聚类类别下的样本量和样本占比
clustering_count = pd.DataFrame(merge_data['渠道代号'].groupby(merge_data['clusters']).count()).T.rename({'渠道代号': 'counts'}) # 计算每个聚类类别的样本量
clustering_ratio = (clustering_count / len(merge_data)).round(2).rename({'counts': 'percentage'}) # 计算每个聚类类别的样本量占比
print(clustering_count)
print("#"*30)
print(clustering_ratio)
clusters 0 1 2 3
counts 154 313 349 73
##############################
clusters 0 1 2 3
percentage 0.17 0.35 0.39 0.08接下来,我们看看每个类别内部最显著的特征:
# 计算各个聚类类别内部最显著特征值
cluster_features = [] # 空列表,用于存储最终合并后的所有特征信息
for line in range(best_k): # 读取每个类索引
label_data = merge_data[merge_data['clusters'] == line] # 获得特定类的数据
part1_data = label_data.iloc[:, 1:7] # 获得数值型数据特征
part1_desc = part1_data.describe().round(3) # 得到数值型特征的描述性统计信息
merge_data1 = part1_desc.iloc[2, :] # 得到数值型特征的均值
part2_data = label_data.iloc[:, 7:-1] # 获得字符串型数据特征
part2_desc = part2_data.describe(include='all') # 获得字符串型数据特征的描述性统计信息
merge_data2 = part2_desc.iloc[2, :] # 获得字符串型数据特征的最频繁值
merge_line = pd.concat((merge_data1, merge_data2), axis=0) # 将数值型和字符串型典型特征沿行合并
cluster_features.append(merge_line) # 将每个类别下的数据特征追加到列表
# 输出完整的类别特征信息
cluster_pd = pd.DataFrame(cluster_features).T # 将列表转化为矩阵
print('{:*^60}'.format('每个类别主要的特征:'))
all_cluster_set = pd.concat((clustering_count, clustering_ratio, cluster_pd),axis=0) # 将每个聚类类别的所有信息合并
all_cluster_set
*******************每个类别主要的特征:*****************
0 1 2 3
counts 154 313 349 73
percentage 0.17 0.35 0.39 0.08
日均UV 2717.42 1390.01 933.015 1904.37
平均注册率 0.005 0.003 0.003 0.003
平均搜索量 0.051 0.152 0.064 0.106
访问深度 0.947 1.168 5.916 0.943
订单转化率 0.007 0.017 0.006 0.009
投放总时间 8.529 8.199 8.77 8.217
素材类型 jpg swf jpg swf
广告类型 banner 不确定 横幅 tips
合作方式 cpc roi cpc cpm
广告尺寸 308*388 600*90 600*90 450*300
广告卖点 满减 打折 直降 打折
上面看着挺累的,不直观,我们图形化输出:
#各类别数据预处理
num_sets = cluster_pd.iloc[:6, :].T.astype(np.float64) # 获取要展示的数据
num_sets_max_min = model_scaler.fit_transform(num_sets) # 获得标准化后的数据
# 画图
fig = plt.figure(figsize=(6,6)) # 建立画布
ax = fig.add_subplot(111, polar=True) # 增加子网格,注意polar参数
labels = np.array(merge_data1.index) # 设置要展示的数据标签
cor_list = ['g', 'r', 'y', 'b'] # 定义不同类别的颜色
angles = np.linspace(0, 2 * np.pi, len(labels), endpoint=False) # 计算各个区间的角度
angles = np.concatenate((angles, [angles[0]])) # 建立相同首尾字段以便于闭合
# 画雷达图
for i in range(len(num_sets)): # 循环每个类别
data_tmp = num_sets_max_min[i, :] # 获得对应类数据
data = np.concatenate((data_tmp, [data_tmp[0]])) # 建立相同首尾字段以便于闭合
ax.plot(angles, data, 'o-', c=cor_list[i], label="第%d类渠道"%(i)) # 画线
ax.fill(angles, data,alpha=2.5)
# 设置图像显示格式
ax.set_thetagrids(angles * 180 / np.pi, labels, fontproperties="SimHei") # 设置极坐标轴
ax.set_title("各聚类类别显著特征对比", fontproperties="SimHei") # 设置标题放置
ax.set_rlim(-0.2, 1.2) # 设置坐标轴尺度范围
plt.legend(loc="upper right" ,bbox_to_anchor=(1.2,1.0)) # 设置图例位置
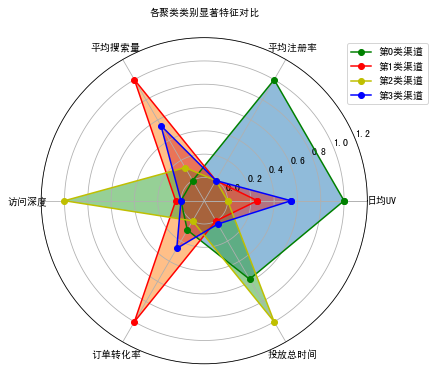
数据结论
Law
从案例结果来看,所有的渠道被分为4各类别,每个类别的样本量分别为:154、313、349 、73,对应占比分别为:17%、35%、39%、8%。
通过雷达图可以清楚的知道:
★
类别1(索引为2类的渠道)
这类广告媒体除了访问深度和投放时间较高,其他属性较低,因此这类广告媒体效果质量较差,并且占到39%,因此这类是主题渠道之一。
业务部门要考虑他的实际投放价值。
类别2(索引为1类的渠道)
这类广告媒体除了访问深度略差,在平均搜索量、日均UV、订单转化率等广告效果指标上表现良好,是一类综合效果较好的渠道。
但是日均UV是短板,较低。无法给企业带来大量的流量以及新用户,这类广告的特质适合用户转化,尤其是有关订单的转化提升。
类别3(索引为0类的渠道)
这类广告媒体的显著特征是日均UV和注册率较高,其“引流”和“拉新”效果好,可以在广告媒体中定位为引流角色。
符合“广而告之”的诉求,适合“拉新”使用。
类别4(索引为3类的渠道)
这类渠道各方面特征都不明显,各个流量质量和流量数量的指标均处于“中等”层次。不突出但是均衡,考虑在各场景下可以考虑在这个渠道投放广告。
