import一个“太极”库,让Python代码提速100倍!-技术圈

文章来源：量子位

众所周知，Python的简单和易读性是靠牺牲性能为代价的——

尤其是在计算密集的情况下，比如多重for循环。

不过现在，大佬胡渊鸣说了：

只需import 一个叫做“Taichi”的库，就可以把代码速度提升100倍！

不信？

来看三个例子。

计算素数的个数，速度x120

第一个例子非常非常简单，求所有小于给定正整数N的素数。

标准答案如下：

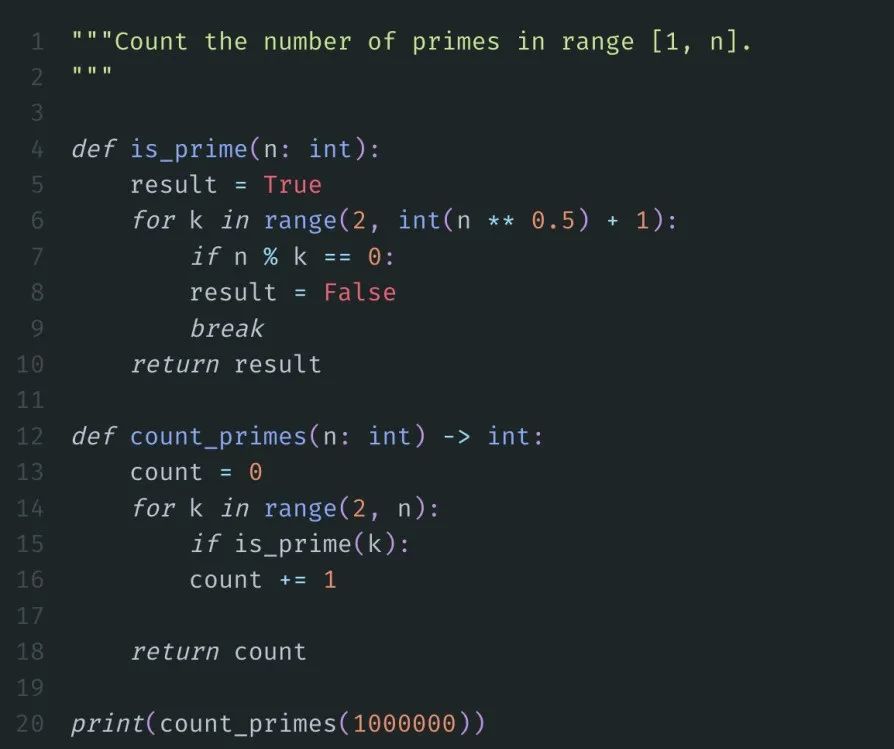
我们将上面的代码保存，运行。

当N为100万时，需要2.235s得到结果：

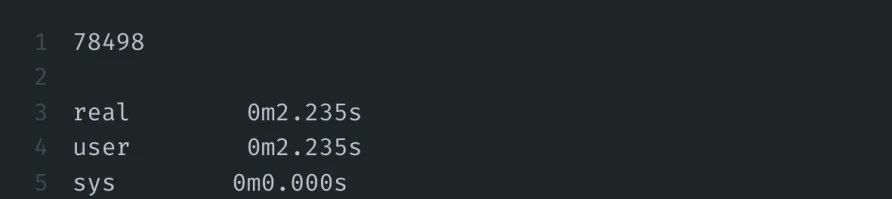
现在，我们开始施魔法。

不用更改任何函数体，import“taichi”库，然后再加两个装饰器：

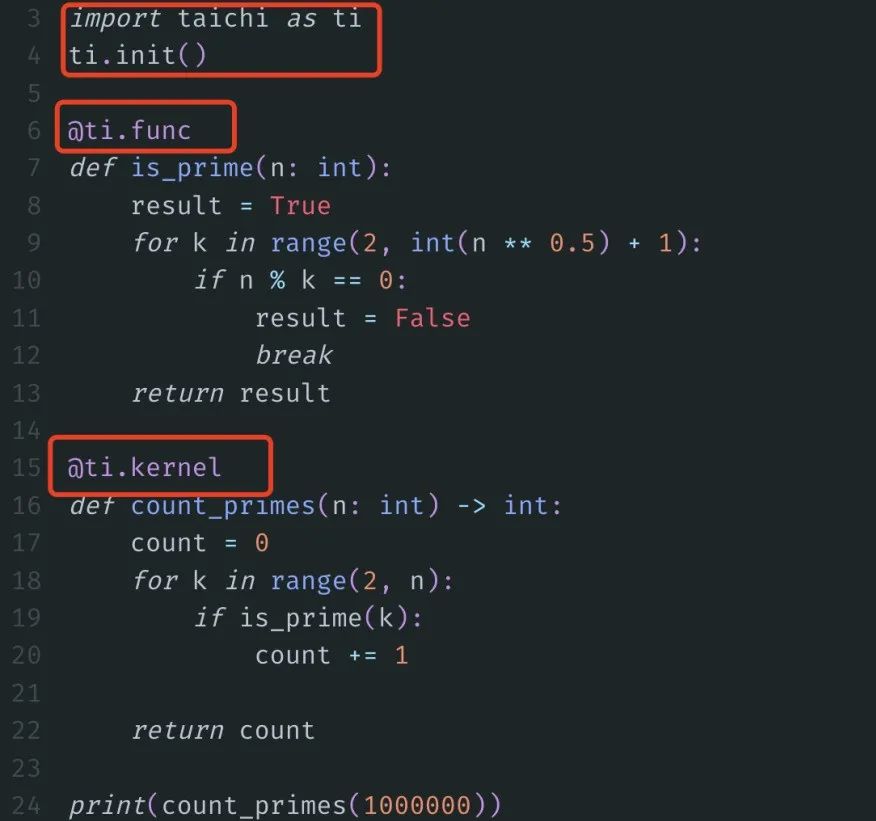
Bingo！同样的结果只要0.363s，快了将近6倍。

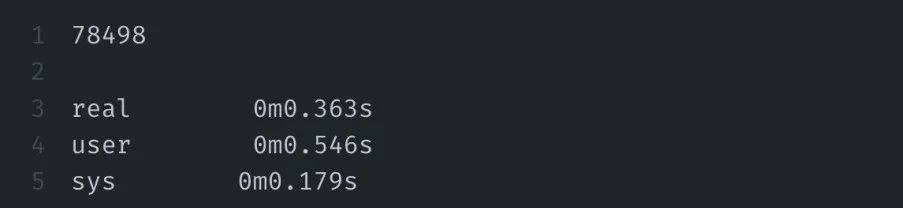
如果N=1000万，则只要0.8s；要知道，不加它可是55s，一下子又快了70倍！

不止如此，我们还可以在ti.init()中加个参数变为ti.init(arch=ti.gpu) ，让taich在GPU上进行计算。

那么此时，计算所有小于1000万的素数就只耗时0.45s了，与原来的Python代码相比速度就提高了120倍！

厉不厉害？

什么？你觉得这个例子太简单了，说服力不够？我们再来看一个稍微复杂一点的。

动态规划，速度x500

动态规划不用多说，作为一种优化算法，通过动态存储中间计算结果来减少计算时间。

我们以经典教材《算法导论》中的经典动态规划案例“最长公共子序列问题（LCS）”为例。

比如对于序列a = [0, 1, 0, 2, 4, 3, 1, 2, 1]和序列b = [4, 0, 1, 4, 5, 3, 1, 2]，它们的LCS就是：

LCS(a, b) = [0, 1, 4, 3, 1, 2]。

用动态规划的思路计算LCS，就是先求解序列a的前i个元素和序列b的前j个元素的最长公共子序列的长度，然后逐步增加i或j的值，重复过程，得到结果。

我们用f[i, j]来指代这个子序列的长度，即LCS((prefix(a, i), prefix(b, j)。其中prefix(a, i) 表示序列a的前i个元素，即a[0], a[1], …, a[i - 1]，得到如下递归关系：

现在，我们用Taichi来加速：

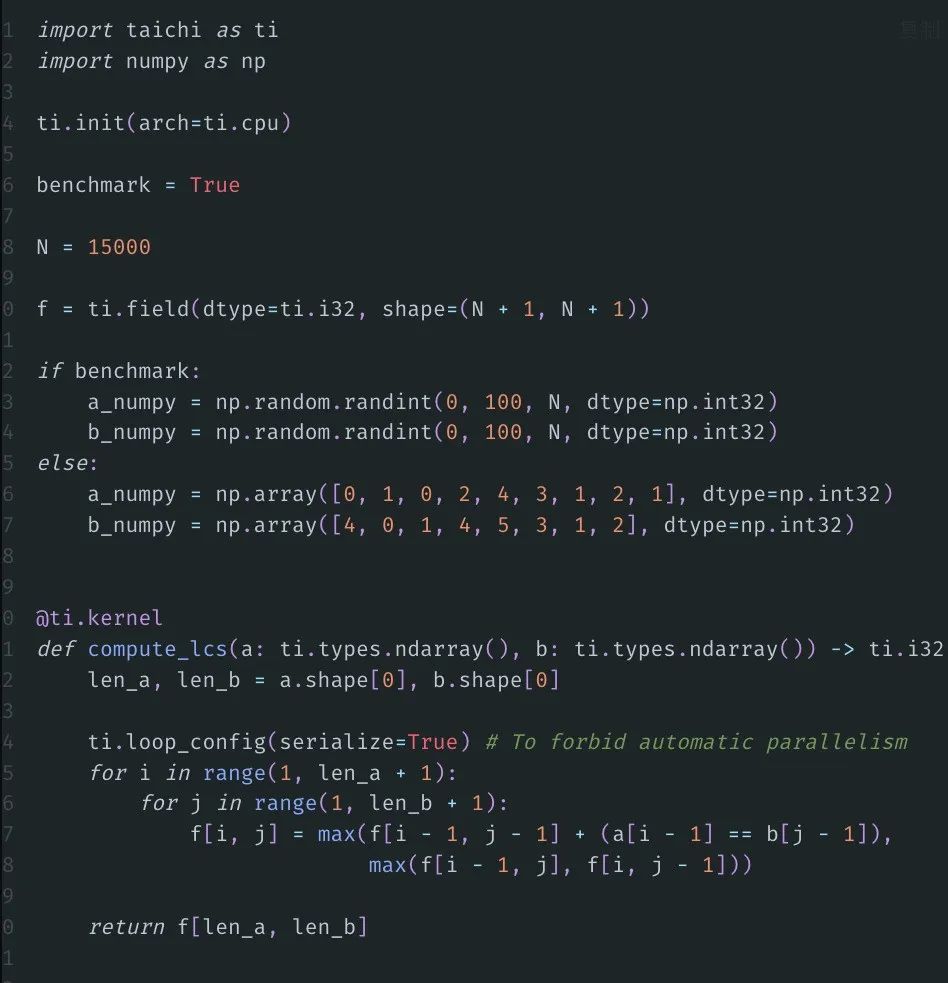
结果如下：

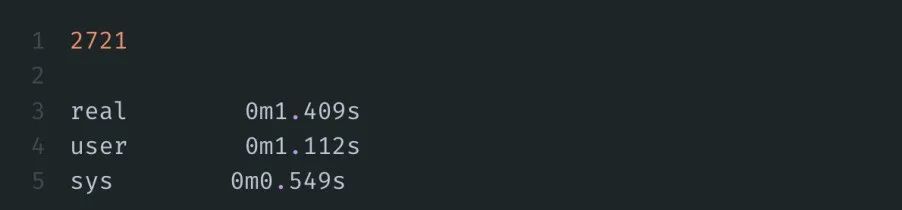
胡渊鸣电脑上的程序最快做到了0.9秒内完成，而换成用NumPy来实现，则需要476秒，差异达到了超500倍！

最后，我们再来一个不一样的例子。

反应 - 扩散方程，效果惊人

自然界中，总有一些动物身上长着一些看起来无序但实则并非完全随机的花纹。

图灵机的发明者艾伦·图灵是第一个提出模型来描述这种现象的人。

在该模型中，两种化学物质（U和V）来模拟图案的生成。这两者之间的关系类似于猎物和捕食者，它们自行移动并有交互：

最初，U和V随机分布在一个域上；

在每个时间步，它们逐渐扩散到邻近空间；

当U和V相遇时，一部分U被V吞噬。因此，V的浓度增加；

为了避免U被V根除，我们在每个时间步添加一定百分比 (f) 的U并删除一定百分比 (k) 的V。

上面这个过程被概述为“反应-扩散方程”：

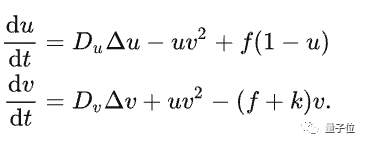
其中有四个关键参数：Du（U的扩散速度），Dv（V的扩散速度），f（feed的缩写，控制U的加入）和k（kill的缩写，控制V的去除）。

如果Taichi中实现这个方程，首先创建网格来表示域，用vec2表示每个网格中U, V的浓度值。

拉普拉斯算子数值的计算需要访问相邻网格。为了避免在同一循环中更新和读取数据，我们应该创建两个形状相同的网格W×H×2。

每次从一个网格访问数据时，我们将更新的数据写入另一个网格，然后切换下一个网格。那么数据结构设计就是这样：

一开始，我们将U在网格中的浓度设置为 1，并将V放置在50个随机选择的位置：

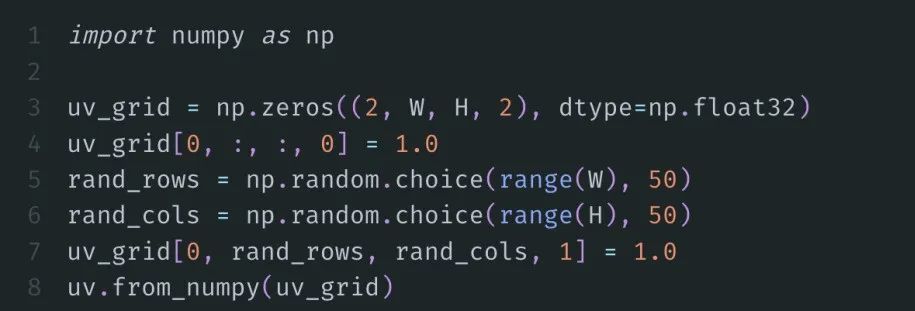
那么实际计算就可以用不到10行代码完成：



    @ti.kernel
def compute(phase: int):
    for i, j in ti.ndrange(W, H):
        cen = uv[phase, i, j]
        lapl = uv[phase, i + 1, j] + uv[phase, i, j + 1] + uv[phase, i - 1, j] + uv[phase, i, j - 1] - 4.0 * cen
        du = Du * lapl[0] - cen[0] * cen[1] * cen[1] + feed * (1 - cen[0])
        dv = Dv * lapl[1] + cen[0] * cen[1] * cen[1] - (feed + kill) * cen[1]
        val = cen + 0.5 * tm.vec2(du, dv)
        uv[1 - phase, i, j] = val