更加精准的时间序列预测--基于Python的 LSTM模型

• 什么是时间序列分析？
• 什么是 LSTM？

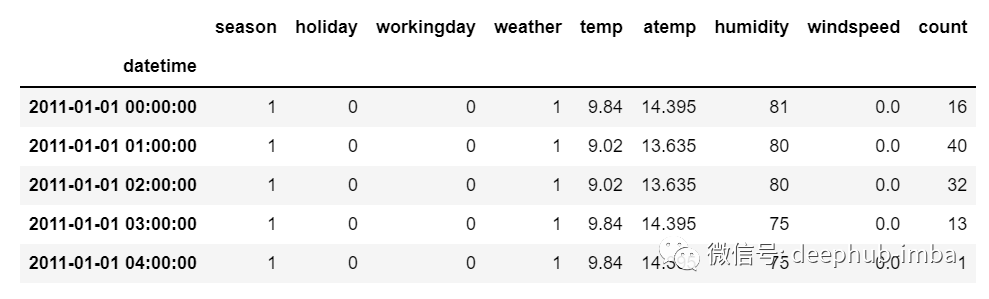
• 单变量时间序列
• 多元时间序列

import numpy as npimport pandas as pdfrom matplotlib import pyplot as pltfrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import LSTMfrom tensorflow.keras.layers import Dense, Dropoutfrom sklearn.preprocessing import MinMaxScalerfrom keras.wrappers.scikit_learn import KerasRegressorfrom sklearn.model_selection import GridSearchCV

df=pd.read_csv("train.csv",parse_dates=["Date"],index_col=[0])df.head()

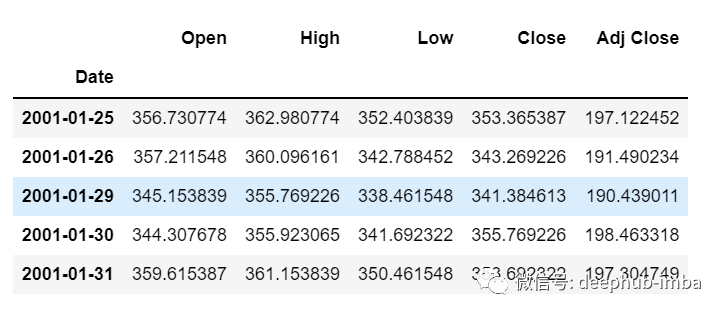
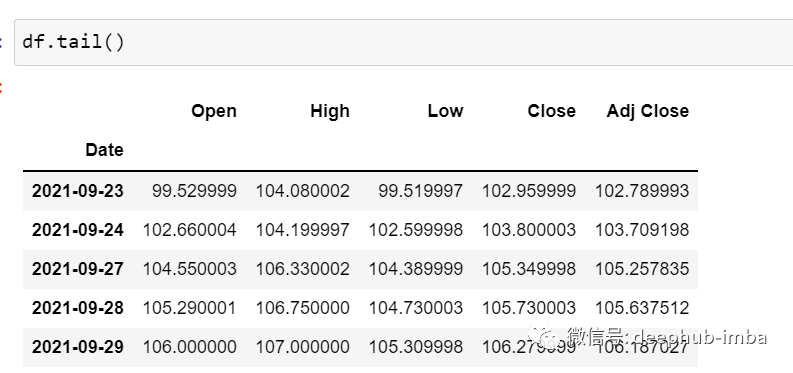
df.tail()

df.shape(5203,5)

test_split=round(len(df)*0.20)df_for_training=df[:-1041]df_for_testing=df[-1041:]print(df_for_training.shape)print(df_for_testing.shape)
(4162, 5)(1041, 5)

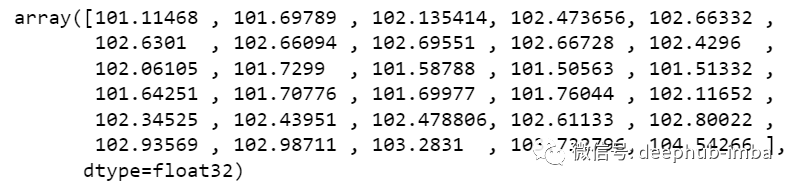
scaler = MinMaxScaler(feature_range=(0,1))df_for_training_scaled = scaler.fit_transform(df_for_training)df_for_testing_scaled=scaler.transform(df_for_testing)df_for_training_scaled

def createXY(dataset,n_past):  dataX = []  dataY = []  for i in range(n_past, len(dataset)):          dataX.append(dataset[i - n_past:i, 0:dataset.shape[1]])          dataY.append(dataset[i,0])  return np.array(dataX),np.array(dataY)
trainX,trainY=createXY(df_for_training_scaled,30)testX,testY=createXY(df_for_testing_scaled,30)

data_X.addend (df_for_training_scaled[i - n_past:i, 0:df_for_training.shape[1]])

print("trainX Shape-- ",trainX.shape)print("trainY Shape-- ",trainY.shape)
(4132, 30, 5)(4132,)
print("testX Shape-- ",testX.shape)print("testY Shape-- ",testY.shape)
(1011, 30, 5)(1011,)

print("trainX[0]-- \n",trainX[0])print("trainY[0]-- ",trainY[0])

trainX — — →trainY
[0 : 30,0:5] → [30,0]
[1:31, 0:5] → [31,0]
[2:32,0:5] →[32,0]

def build_model(optimizer):  grid_model = Sequential()  grid_model.add(LSTM(50,return_sequences=True,input_shape=(30,5)))  grid_model.add(LSTM(50))  grid_model.add(Dropout(0.2))  grid_model.add(Dense(1))
grid_model.compile(loss = 'mse',optimizer = optimizer)  return grid_modelgrid_model = KerasRegressor(build_fn=build_model,verbose=1,validation_data=(testX,testY))
parameters = {'batch_size' : [16,20],            'epochs' : [8,10],            'optimizer' : ['adam','Adadelta'] }
grid_search = GridSearchCV(estimator = grid_model,                          param_grid = parameters,                          cv = 2)

(trainX.shape[1],trainX.shape[2]) → (30,5)

grid_search = grid_search.fit(trainX,trainY)

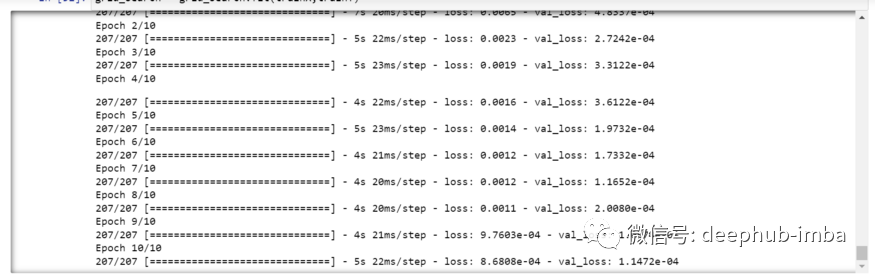
grid_search.best_params_
{‘batch_size’: 20, ‘epochs’: 10, ‘optimizer’: ‘adam’}

my_model=grid_search.best_estimator_.model

prediction=my_model.predict(testX)print("prediction\n", prediction)print("\nPrediction Shape-",prediction.shape)

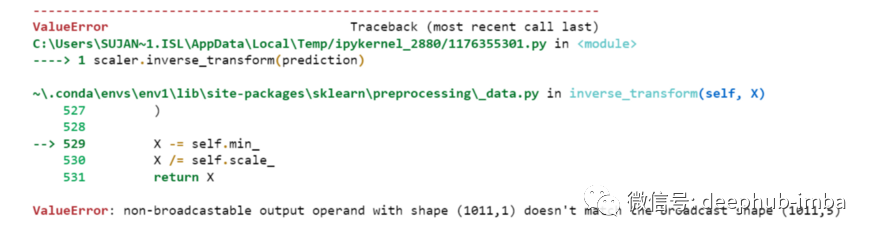
scaler.inverse_transform(prediction)

prediction_copies_array = np.repeat(prediction,5, axis=-1)

prediction_copies_array.shape(1011,5)

pred=scaler.inverse_transform(np.reshape(prediction_copies_array,(len(prediction),5)))[:,0]

original_copies_array = np.repeat(testY,5, axis=-1)original=scaler.inverse_transform(np.reshape(original_copies_array,(len(testY),5)))[:,0]

print("Pred Values-- " ,pred)print("\nOriginal Values-- " ,original)

plt.plot(original, color = 'red', label = 'Real Stock Price')plt.plot(pred, color = 'blue', label = 'Predicted Stock Price')plt.title('Stock Price Prediction')plt.xlabel('Time')plt.ylabel('Google Stock Price')plt.legend()plt.show()

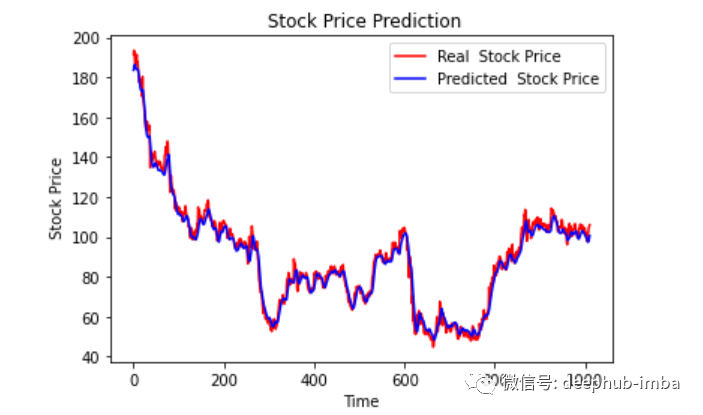
df_30_days_past=df.iloc[-30:,:]df_30_days_past.tail()

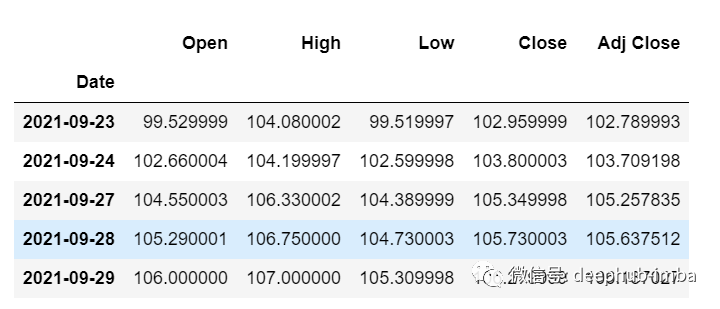
df_30_days_future=pd.read_csv("test.csv",parse_dates=["Date"],index_col=[0])df_30_days_future

df_30_days_future["Open"]=0df_30_days_future=df_30_days_future[["Open","High","Low","Close","Adj Close"]]old_scaled_array=scaler.transform(df_30_days_past)new_scaled_array=scaler.transform(df_30_days_future)new_scaled_df=pd.DataFrame(new_scaled_array)new_scaled_df.iloc[:,0]=np.nanfull_df=pd.concat([pd.DataFrame(old_scaled_array),new_scaled_df]).reset_index().drop(["index"],axis=1)

full_df_scaled_array=full_df.valuesall_data=[]time_step=30for i in range(time_step,len(full_df_scaled_array)):  data_x=[]  data_x.append(    full_df_scaled_array[i-time_step :i , 0:full_df_scaled_array.shape[1]])  data_x=np.array(data_x)  prediction=my_model.predict(data_x)  all_data.append(prediction)  full_df.iloc[i,0]=prediction

new_array=np.array(all_data)new_array=new_array.reshape(-1,1)prediction_copies_array = np.repeat(new_array,5, axis=-1)y_pred_future_30_days = scaler.inverse_transform(np.reshape(prediction_copies_array,(len(new_array),5)))[:,0]print(y_pred_future_30_days)