实践教程 | 在yolov5上验证一些不成熟的想法

一、起因

在迁移mxnet训练代码的时候，很长一段时间结果都无法对齐，于是我不得不又重新认真的读了一下之前撸的mxnet代码，在看的过程中发现了很多之前留下来的备注。我都已经不记得是否有尝试过，索性就结合最近的一些思路，看看自己的一些想法是否科学。

二、分析

讨论不同的检测方法，核心点就是目标分配和loss函数的使用了。毕竟数据准备，网络结构，训练技巧等等大家都能用。所以先简单叙述一下我的认知，为后续做个铺垫。

1、目标分配

• 在传统方法中，我们一般使用图像金字塔+滑动窗口进行图像切分，然后使用传统的特征抽取方法进行分类。这个时候滑窗和目标达到一定的IOU我们就认定为正样本，低于某个值就是负样本，中间值直接舍去。

• 在基于anchor的方法中，我们一般使用密集铺设的anchor和目标计算IOU，大于某个值作为正样本，小于某个值为负，中间值舍去。这时候就跳出了一些略微特殊的方法，比如yolo计算的是wh的IOU，然后忽略样本是预测结果和标签的IOU大于某个值（正样本不改变，只改负样本）。

• 在anchor free的方法中（或者很多方法可以称为point anchor），我们可以使用高斯核，可以使用固定范围，可以自适应等等来区分正负样本。

• 端到端的方法目前我认为还不是很成熟，也就不说了。

2、损失函数

损失函数其实单独拿出来说不是特别科学，因为损失函数需要和具体的样本划分以及标签设置有关系。比较常见的就是交叉熵，l1 ，l2，soomth l1，focal家族等等。

三、尝试

我这次所有的尝试都是基于修改版本的yolov5代码。原版的yolov5正负样本采用wh和anchor的比例最大值来决定。在可视化训练标签和样本后发出几个疑问。

1）样本的划分是否合理？

首先看几个示例

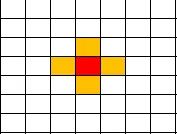
红色表示目标中心在特征图上的位置，每次都会取，也是yolo前几代的正样本点。橙色点是yolov5新增加的，每次会从4个橙色点中取出两个相邻的结果，如示例。

现在考虑一些问题：

1、橙色点的贡献应该是均等的吗？例如x=3.51和x=3.99，在取值的时候都会取x=3,4这两个点。当目标比较大的时候贡献均等与否影响不大，但是目标较小的时候是否也能均等贡献？

2、不同大小的目标都只取3个点吗？按照yolov5的设置，在同一层上的目标，最大的比例宽度为16倍。简单解释一下，例如Anchor的w为8，设置的比例阈值为4，那么最小的w为2，最大的w为32。当我们在同一层上进行预测的时候，小目标可能跨度都不够2个网格，大目标跨度是小目标的数倍。那我们都取同样的正样本点，甚至正样本点都不在目标范围内，这是否合适？

3、除去正样本就是负样本这样合适吗？还是刚刚的例子x=3.51时，我们认为3,4为正样本点，2为负样本点。但实际上2,4到中心的差距只差0.02 他们的贡献就应该一正一负吗？

4、直接按照宽高比例取，导致某些点被重复使用这样影响大吗？我们在取点的时候不会判断是否被之前的目标使用，而是按照标签去直接取点运算。这就会导致某些点被多次使用，尤其是目标比较密集的时候。这点在和yolov5的作者讨论的时候也说到了，后面会有当时讨论的修改方案和结果。

5、如果我们选择的Anchor不合理，就会导致某些目标同时出现在所有Anchor或者说所有预测层上，这样强制学习是否可靠？

6、某些标签会被漏掉，例如宽高比例差距很大的数据。漏掉的如何补充进训练数据？

再看一个yolov5训练的特征可视化结果：

从特征可视化结果来看，整体倾向于标签选择方式，类似直角三角形的直角边为高可信度区域。但这就有个问题靠近直角边中间的区域，以及反向区域，就应该是低置信度吗？

pytorch 特征可视化：https://zhuanlan.zhihu.com/p/388435039

2）尝试修正不合理

1、关于不同点的贡献是否均等的问题，尝试使用距离比例来解决，选定的正样本点，以到实际目标中心点的距离来决定正样本指数的比例，如x=3.51和x=3.99则比例分别为0.51和0.99；当x=3.49和x=3.01时比例为0.51和0.99（注意这里是取的3,2了，不是3,4）。

2、针对不同目标大小使用fcos中的方式，设置一个范围然后取半径内的点。这样就会出现某些目标只会有中心一个点，有的目标可能有半径3范围内的16个点。

3、直接非正即负的方式替换为预测值和真实标签大于某个值得时候，ignore掉负样本。

4、重复点采用两种方式解决，第一种是直接暴力去重使用torch.unique加上一堆操作来实现，第二种是根据预测结果的iou，选择高iou的结果。

5、合理设置Anchor，相邻层的Anchor比例设置为宽高阈值以上。

6、学习前几代yolo的操作，强制把漏掉的样本加入训练中。

3）看上去无关的尝试

1、别人说好用的loss，都拿来试一下，比如GFL这种神器，比如VFL这种不知名的武器，比如OHEM操作等等。

2、Anchor的数量和值，是否真的影响非常大。

3、各种超参数的组合拳。

4）尝试的结果

1、超参数的调整基本没有意义，影响较大的是影响loss比例的参数，这个需要确保yolov5的box loss和obj loss最终的比例大致在1:2左右，这样会收敛到比较好的结果。

2、Anchor选择
- [192,240, 384,480, 512,640] # P5/32
- [48,60, 96,120, 144,180] # P4/16
- [12,15, 24,30, 36,45] # P3/8

- [192,240] # P5/32
- [48,60] # P4/16
- [12,15] # P3/8

这两组Anchor跑出来的训练结果基本是一致的，可以看到Anchor选择正好是宽高阈值界限，所以合理设置Anchor的大小是重要的，Anchor数量就影响较小。

3、花里胡哨的样本选择方式，需要配合loss的调整才能使用，如果只是直接修改样本信息，结果可能会不如原版本。

4、同上一条，直接修改loss函数也不一定适用，例如focal类似的操作，强调难易样本的不均等对待，这时候因为yolov5的非正即负的样本选择方式，就会导致使用focal的时候模型进入迷惑状态，最终性能会下降。

5、不同样本位置和宽高，进行加权以及范围选择。有效但是影响比较小。

6、对原始yolov5中的重复取点进行去除操作，几乎没有影响，我的理解是作者的操作会导致样本数量非常多，例如一个样本可能生成27个采样点，就算有一部分被重复使用，影响也不大。

7、GFL这类操作是有意义的，就算你不配合修改样本划分策略。使用这类方法也能稳定提升结果，尤其是小目标性能，VFL在小目标和难例上的表现又比GFL好一些。

四、总结

拿经典的人脸检测任务梭哈了一把，怼上各种合理的，不合理的操作之后。我们的网络性能较之前在wider face hard上提升了5个点（这里是在yolov5原版的基础上提升的，但是可能和我用的是小模型，加上hard数据比较难导致的，不一定有代表意义）。模型大概就是一个朴实无华的mini vgg + fpn，没有反卷积，3个输出层，每个点输出一个Anchor，整体结构非常清新。在224X224分辨率下大概是150M的算力。如果替换为depth wise这类型的操作，理论算力下降会很明显，但是npu上会变慢，所以我们所有卷积都是普通卷积。

模型大概就是这种全普通卷积+fpn操作

关于白嫖和自己的想法：

1、既然是白嫖就老老实实的白嫖，不要期望自己在别人的基础上做出突出的改善。

2、漂亮的可视化结果或者一个好的故事，也许只能安慰一下自己空虚的心灵，并不一定提升模型的结果。

3、样本选择和loss选择是一个联动的过程。孤立任何一方去修改都可能事倍功半甚至是无用功。

4、大力很多时候能出奇迹，一些方法不是不适合，而是不适合你的训练参数或者模型结构。

五、不知道咋取名

在刚毕业的时候，我和我师傅两个就鼓捣出了现在非常流行的Anchor free检测器，和《centernet：objects as points》文章的思路比较相似。然鹅最终取没有在公司的主流任务中使用(被Rcnn系列打败了)。这也导致了我一直以来只会yolo这种套路的检测方案，不会ssd(强行找个借口)。

回想一下我们当时的做法：

a、将输入resize到两个分辨率上，一大一小。

b、梭哈图片得到两个特征图，然后按照特征图上目标的大小给予置信度标签，以及边框标签。

c、用同一个backbone分别训练两个固定分辨率的数据。

看一下当时我们没用上，但是有比较大的意义的技术：

a、fpn，特征金字塔，特征融合。

b、focal loss或者软化标签。

c、iou 感知替换置信度标签或者类似center ness这类。

看上去似乎修改不大，但都解决了一部分检测中比较核心的标签分配问题。

不同大小的目标怎么分；不同难度样本怎么分；边框和置信度训练使用割裂的问题。

现在回想起来，觉得自己思考还是太简单了，很多问题发现了但是并没有尝试找到合理的解决方案，所以一直这么菜鸡。

推荐阅读
“拍一拍” 能撤回了 ！！！
5款Chrome插件，第1款绝对良心！
为开发色情游戏，这家公司赴日寻找AV女优拍摄，期望暴力赚钱结果...
拼多多终于酿成惨剧
华为阿里下班时间曝光：所有的光鲜，都有加班的味道

关于程序员大白

程序员大白是一群哈工大，东北大学，西湖大学和上海交通大学的硕士博士运营维护的号，大家乐于分享高质量文章，喜欢总结知识，欢迎关注[程序员大白]，大家一起学习进步！