点击上方【AI人工智能初学者】，选择【星标】公众号

期待您我的相遇与进步

本文提出Normalizer-Free方法，可用于设计没有激活归一化层的深度残差网络！并能直接应用于ResNet、RegNet等网络，在相同FLOP预算下，性能可比肩EfficientNet，代码已开源！！！
作者单位：DeepMind

1 简介

Batch Normalization几乎是所有最新图像分类器中的关键组件，但同时也带来了实际挑战：它打破了Batch内训练样本之间的独立性，可能会导致计算和内存的开销，并经常导致意外的错误。

基于对初始化时深度ResNet的最新理论分析，本文提出了一套简单的分析工具来表征前向信号的传播，并利用这些工具设计高性能无需激活归一化层的ResNet。本方法的关键是最近提出的Weight Standardization的改编版本。本文所提出的分析工具展示了该技术如何在确保具有ReLU或Swish激活功能的同时每通道不会随网络深度增长而丢失信号。

本文主要贡献：

• 1 介绍了Signal Propagation Plots(SPPs):一组简单的可视化方法，帮助查看深度残差网络的前向传递初始化时信号传播；
• 2 提出了比例权重标准化，阻止了均值信号的增长，使得性能得到大幅提升；
• 3 将normalization-free结构与Scaled Weight Standardization一起应用于ImageNet上的ResNets，在此基础上首次实现了在288层的网络上比批量标准化的ResNets更好的性能。
• 4 将normalization-free应用于RegNet架构。通过将这种架构与复合缩放策略相结合开发了没有标准化层的模型，并达到SOTA效果。

2 背景动机

BatchNorm和skip连接的结合使得从业者能够训练具有数百或数千层的Resnet。为了理解这种效应，许多论文在初始化时分析了信号在normalized ResNets中的传播。在最近的一项工作中，最近有研究表明，在高斯初始化的normalized ResNets中，相对于Skip Path上的激活规模，第 Residual Branch上的激活被 因子抑制。这使得deep ResNets中的Residual块在初始化时偏向于identity function，确保了表现良好梯度的传递。

在unnormalized网络中，可以通过在每个Residual Branch的末尾引入一个可学习的标量，初始化为零来保持这一好处。这个简单的改进足以在没有normalized的情况下训练带有数千个层的深度网络。然而，尽管该方法易于实现，并在训练集上取得了很好的收敛性，但与well-tuned baselines相比，它的测试精度仍低于normalized网络。

这些来自batch-normalized ResNets研究的idea也得到了unnormalized网络理论分析的支持。这些研究表明，在具有identity skip connections的ResNets中，如果信号在前向传递时不出现梯度爆炸，梯度在后向传递时既不会爆炸也不会消失。Hanin&Rolnick在自己的研究中总结得出结论，将残差分支上的隐藏激活乘以一个因子 或更小，其中d表示网络深度，足以保证初始化时的可训练性。

为了抵消BatchNorm在不同情况下的局限性，已经提出了一系列替代的规范化方案，每个方案都在隐藏激活的不同组件上运行。这包括LayerNorm, instancnorm, GroupNorm等等。

虽然这些替代方案消除了对batch sizes的依赖，并且通常在非常小的batch sizes上比BatchNorm工作得更好，但它们也引入了自己的限制，比如在推理时引入额外的计算成本。

此外，对于图像分类，这些替代方案的测试精度往往低于well-tuned baselines。本文作者也注意到GroupNorm与Weight Standardization的结合最近被确定为ResNet-50中BatchNorm的一个比较好的替代方案。

3 Signal Propagation Plots

最近有论文从理论上分析了ResNets中的信号传播，但在设计新模型或提出对现有架构的修改时，实践者很少从经验上评估特定深度网络中不同深度隐藏激活的规模。相比之下，本文作者发现，在一批随机高斯输入或真实训练实例的条件下，绘制网络内不同点隐藏激活的统计数据是非常有益的。

这种实践能够在启动一个注定失败的训练运行之前，立即检测到实现中隐藏的bug。

因此，作者通过引入信号传播图(SPPs)来可视化信号在深度ResNets的前向传递上的传播。

假设identity residual blocks形式为 ，其中 表示第 块的输入， 表示第 residual分支计算的函数。考虑4维的输入和输出张量，其维数用NHWC表示，其中N表示Batch，C表示Channel，H和W表示两个空间维数。为了生成spp，作者根据网络初始化方案初始化一组权值，然后向网络提供一批单位高斯分布的输入样本。然后，在每个residual blocks的输出处绘制以下隐藏的激活统计信息：

• Average Channel Squared Mean：通过NHW轴计算平均值的平方，然后在C轴上求平均值。在一个信号传播良好的网络中，期望每个通道上的平均激活，在一批例子中平均，接近于零。这里有必要测量平均值平方的平均值，因为不同通道的平均值可能有相反的符号。
• Average Channel Variance：通过在NHW轴上取通道方差，然后在C轴上取平均值来计算得到。这最能提供信息的信号大小测量，并清楚地显示信号梯度的爆炸或弥散。
• 在Residual分支的末端Average Channel Variance：在与skip path合并之前。这有助于评估Residual分支上的层是否被正确初始化。

spp并没有捕捉到信号传播的所有特性，它们只考虑了正向传递的统计信息。但是只要正向传递的信号表现良好，反向传递通常不会爆炸或消失。

举例如下：

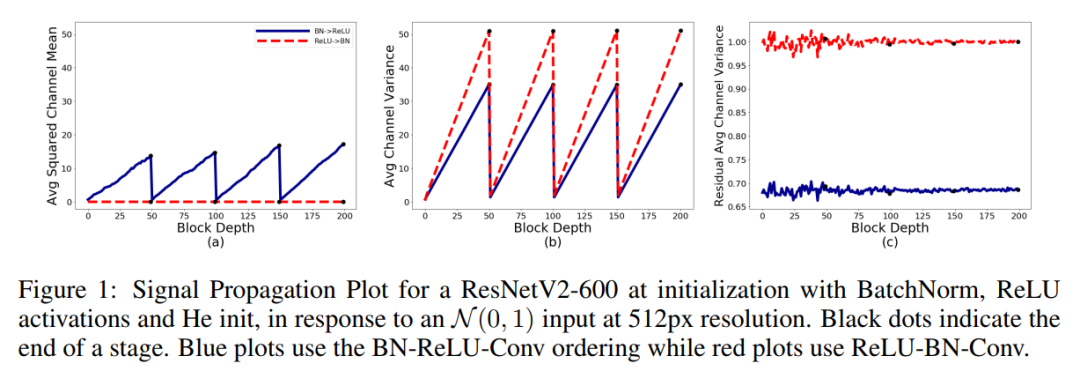
在Figure 1中展示了600层预激活的带有BatchNorm、ReLU激活和He初始化的ResNet的SPP。比较了标准的BN-ReLU-Conv排序和较不常见的ReLU-BN-Conv排序。

首先，实验发现Average Channel Variance在给定阶段会随深度线性增长，并且在每个transition block 上重置到接近1的固定值。这里出现线性增长是因为在初始化时激活的方差满足：，而BatchNorm确保每个residual分支结束时激活的Variance与深度无关(可以看出上图的b中在block结束时出现了正交的坐标，因此与Depth无关)。在每个transition block上重置Variance，因为在这些块中，Skip Connection在标准化输入上操作的卷积代替，消除了前面块中Skip Path上的任何信号增长。

在BN-ReLU-Conv在训练时Average Squared Channel Means显示类似的规律在transition blocks之间随深度线性增长。期望BatchNorm以激活为中心。然而，通过这种排序在一个residual分支上的最终卷积接收到一个整流具有正均值的输入。这会导致分支在任何单个通道上的输出也具有非零均值，并解释了为什么 在所有深度上都约等于0.68。尽管这种均值偏移会被后续residual分支中的规范化层显式抵消，但当试图删除规范化层时，它将产生严重的后果。与之相反，ReLU-BN-Conv训练时在避免均值转移问题的同时具有同等稳定性，这里对于所有的 而言 约等于1。

4.NF ResNets

通过使用spp分析，本文作者开发了不带归一化层的ResNet的变体，它不仅具有良好的信号传播能力，并且在训练期间是稳定的，并获得了与批量归一化后的ResNet差不多的效果和精度。首先，对于standard initializations，BatchNorm以与输入的标准差成比例的因子将每个residual block输入进行downscales。其次，每个residual block使信号的方差增加一个Contant Factor。这里使用形式为 的残差块来模拟，其中 表示第一个残差块的输入， 表示第一个残差分支。

• 用于残差分支计算的函数，这里会被参数化为初始化时的方差，即 。这个约束使推理网络中的信号增长不受深度的影响，并可以分析与估计方差。

• 是一个为 固定的标量，初始化时激活 的预期经验标准差。这保证了 的输入具有unit variance。

• 是控制块间方差增长率的标量超参数。

根据 解析计算剩余块的期望经验方差，初始期望方差 ，并设 。由于shortcut convolution接收到规范化输入，规范化ResNets中的信号方差在每个transition layer重置。

为了确保每个阶段开始时的单位信号方差 ，这里通过让transition layer中的shortcut convolution操作 ，而不是 来模拟这种重置。这种简单的缩放策略的残差网络称为NF-ResNets。

4.1 包含均值漂移的ReLU

在之前的实验中作者观察到Average Channel Squared Mean随着深度的增加而迅速增长并达到或超过Average Channel Squared Mean的大值，这表明了一个较大的均值偏移，即不同训练输入的隐藏激活是紧密相关的；正如前面所观察到的BN-ReLU-Conv网络，残差分支的经验方差规模始终小于1。

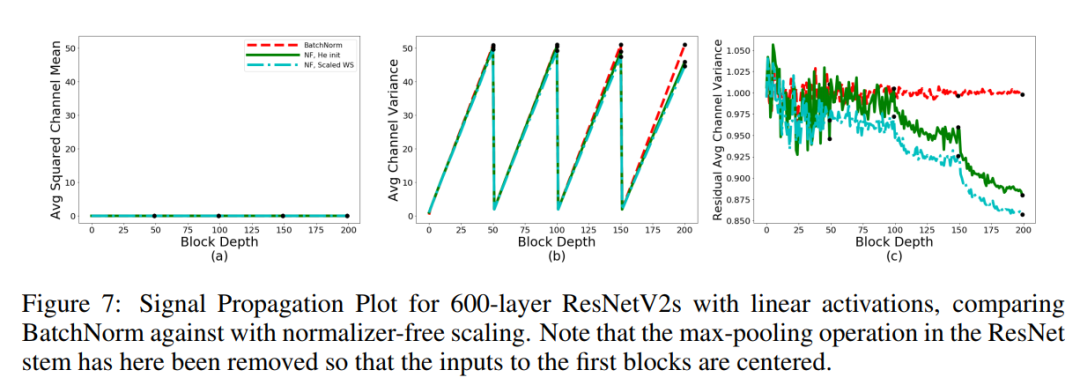
为了确定这些现象的来源，在Figure 7中，作者为线性化的ResNetV2-600提供了一个类似的SPP，该版本没有ReLU激活功能。当移除ReLU激活时，所有区块深度的Average Channel Squared Mean保持接近于零，residual分支的经验方差在1上下波动。这引发了以下问题:为什么重新激活会导致Channel平均激活的规模增长?

为了对该现象有一个直观的认识，考虑变换 ，其中 是arbitrary and fixed， 是一个激活函数，以组件方式作用于输入 。因此， 可以是任何常用的激活函数，如ReLU、tanh、SiLU等。对所有i,设 , ，可以直接表示输出的任意单个单位 的期望值和方差 为:

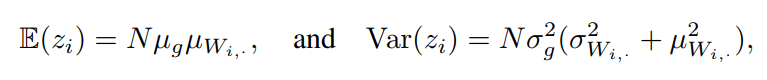
其中， 和 分别为 的第 行均值和标准差;

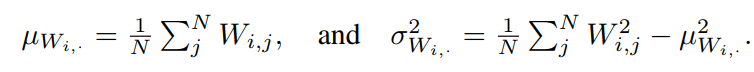
假设 为ReLU激活函数，即 。然后 ，这意味着对线性层的输入具有正的均值(忽略所有输入小于或等于0时的边界情况)。特别地，如果 ，那么 。因为 ,如果 也是非零的，那么变换的输出 也将是一个非零的均值。

重要的是，即使从以0为中心的分布中采样 ，从这个分布中得出的任何特定权重矩阵几乎肯定会有一个非零的经验均值，因此任何特定通道上residual分支的输出将具有非零的均值。因此，这个具有he初始化权值的简单的NF-ResNet模型往往不稳定，并且随着深度的增加训练变得越来越困难。

4.2 Scaled Weighted Standardization

为了防止均值偏移的出现，并确保残差分支 保持方差，作者提出了Scaled Weighted Standardization，该标准化也与中心权重标准化密切相关。重新参数化卷积层：

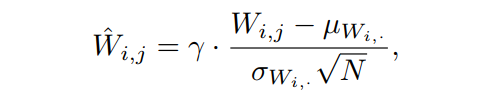
其中的均值 和方差 是通过卷积滤波器的扇入范围计算的。从高斯权值初始化潜在参数W，而 是一个固定常数。在整个训练过程中将这个约束作为网络向前传递的可微分操作。使用缩放 的变换的输出 ，对所有 的期望值 ，从而消除了均值偏移。

此外，方差 ，这意味着对于一个正确选择的 ，它依赖于非线性g，该层将保持方差。

Scale Weight标准化在训练以及Inference的过程中性价比都很高，不引入批处理元素之间的依赖性，训练和测试也没有差异，而且它的实现在分布式训练中没有区别。这些理想的特性使它成为替代BatchNorm的选择。

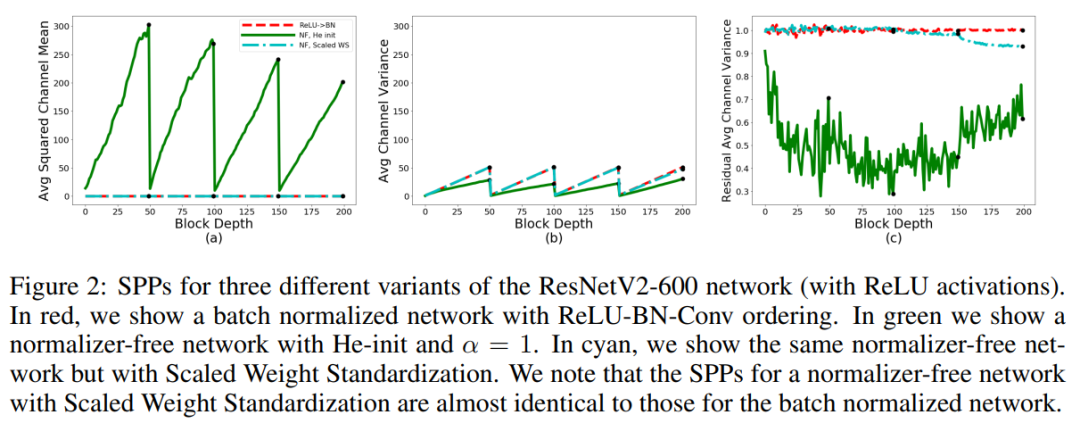
Figure 2中显示的是采用缩放WS的normalizer-free ResNet-600的SPP(青色)。正如所看到的，缩放权重标准化消除了初始化时Average Channel Squared Mean的增长。事实上，对于使用ReLU-BN-Conv的批归一化网络，spp几乎是相同的，如红色所示。注意，选择常数 是为了确保residual分支上的Channel方差接近于1。由于0 padding，residual分支的方差在网络的末端附近略有衰减。

4.3 确定Nonlinearrity-Specific常量

最后，需要确定增益 的值，以确保在初始化时residual分支上隐藏激活的方差接近1。注意， 的值将取决于在网络中使用的specific nonlinearity。假定非线性的输入 服从 。对于ReLU网络，这意味着输出 将从修正的高斯分布 中采样。

因为 ，为了确保 ，设 。当网络宽度很大时， 服从 通常不正确，除此之外作者发现这种近似在实践中很好地工作。

对于简单的非线性，如ReLU或tanh，当 从单位法向量得出时，非线性 的解析方差可能是已知的或容易推导的。

对于其他非线性，如SiLU(最近以Swish的形式推广)，分析确定方差可能涉及求解困难的积分，甚至可能没有解析形式。

在实践中发现从高斯分布中得到许多N维向量 ，计算每个向量的经验方差 ，并对这个经验方差的平均值取平方根，这样一个简单的过程在数值上近似这个值是足够的。

4.4 模块构建与约束松弛

本文方法通常要求在网络中使用的任何额外操作保持良好的信号传播，这意味着许多常见的构建块必须修改。与选择 值一样，必要的修正可以通过分析或经验来确定。

例如，Squeeze-and-Excitation操作(S+E)，，涉及到[0,1]中激活的乘法，容易使信号衰减，使模型不稳定。这个衰减在normalizer-free ResNet中通过SPP可以明显看到：

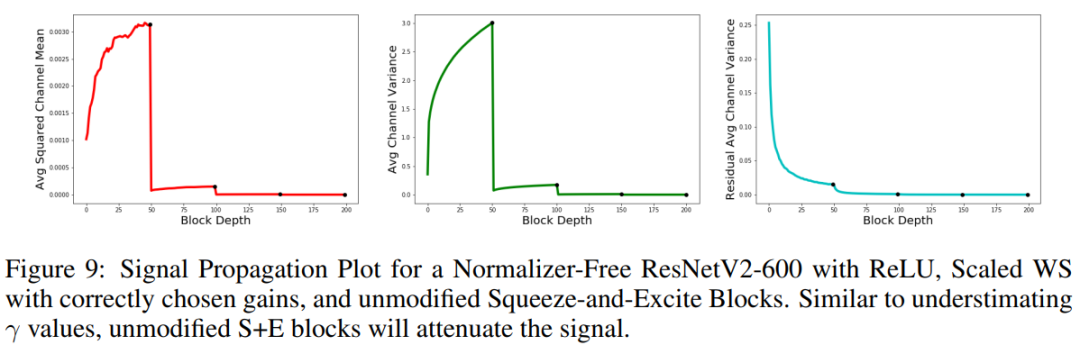
如果单独检查这个操作使用简单的数值发现预期的方差是0.5,表明只需要输出乘以2恢复良好的信号传播。实践验证了这种简单的改变足以恢复训练的稳定性。

在实践中发现，对任何给定的操作进行类似的简单修改就足以保持良好的信号传播，或者网络对由操作引起的退化有足够的鲁棒性，无需修改就能很好地训练。作者也探索了可以在多大程度上放松约束，仍然保持稳定的训练。

作为一个例子，为了恢复正常卷积的一些表达能力，作者向缩放的WS层引入了可学习的仿射增益和偏差(增益应用于权值，而偏差被添加到激活，这是典型的)。虽然可以约束这些值来加强良好的信号传播，例如，将输出与增益值成比例地缩小一个标量，但这对稳定训练是不必要的，当这些参数自由变化时，稳定性不会受到影响。

作者也发现在residual分支初始化为0的末端使用一个可学习的标量乘子在训练超过150层的网络时是有帮助的，即使在计算 时忽略这个修改。在最终的模型中在不影响训练稳定性的情况下使用了几个这样的松弛。

Normalization-Free Block源码：

class NormalizationFreeBlock(nn.Module):
    """Normalization-free pre-activation block.
    """

    def __init__(
            self, in_chs, out_chs=None, stride=1, dilation=1, first_dilation=None,
            alpha=1.0, beta=1.0, bottle_ratio=0.25, efficient=True, ch_div=1, group_size=None,
            attn_layer=None, attn_gain=2.0, act_layer=None, conv_layer=None, drop_path_rate=0., skipinit=False):
        super().__init__()
        first_dilation = first_dilation or dilation
        out_chs = out_chs or in_chs
        # EfficientNet-like models scale bottleneck from in_chs, otherwise scale from out_chs like ResNet
        mid_chs = make_divisible(in_chs * bottle_ratio if efficient else out_chs * bottle_ratio, ch_div)
        groups = 1 if group_size is None else mid_chs // group_size
        if group_size and group_size % ch_div == 0:
            mid_chs = group_size * groups  # correct mid_chs if group_size divisible by ch_div, otherwise error
        self.alpha = alpha
        self.beta = beta
        self.attn_gain = attn_gain

        if in_chs != out_chs or stride != 1 or dilation != first_dilation:
            self.downsample = DownsampleAvg(
                in_chs, out_chs, stride=stride, dilation=dilation, first_dilation=first_dilation, conv_layer=conv_layer)
        else:
            self.downsample = None

        self.act1 = act_layer()
        self.conv1 = conv_layer(in_chs, mid_chs, 1)
        self.act2 = act_layer(inplace=True)
        self.conv2 = conv_layer(mid_chs, mid_chs, 3, stride=stride, dilation=first_dilation, groups=groups)
        if attn_layer is not None:
            self.attn = attn_layer(mid_chs)
        else:
            self.attn = None
        self.act3 = act_layer()
        self.conv3 = conv_layer(mid_chs, out_chs, 1)
        self.drop_path = DropPath(drop_path_rate) if drop_path_rate > 0 else nn.Identity()
        self.skipinit_gain = nn.Parameter(torch.tensor(0.)) if skipinit else None

    def forward(self, x):
        out = self.act1(x) * self.beta

        # shortcut branch
        shortcut = x
        if self.downsample is not None:
            shortcut = self.downsample(out)

        # residual branch
        out = self.conv1(out)
        out = self.conv2(self.act2(out))
        if self.attn is not None:
            out = self.attn_gain * self.attn(out)
        out = self.conv3(self.act3(out))
        out = self.drop_path(out)
        if self.skipinit_gain is None:
            out = out * self.alpha + shortcut
        else:
            # this really slows things down for some reason, TBD
            out = out * self.alpha * self.skipinit_gain + shortcut
        return out

5 实验与分析

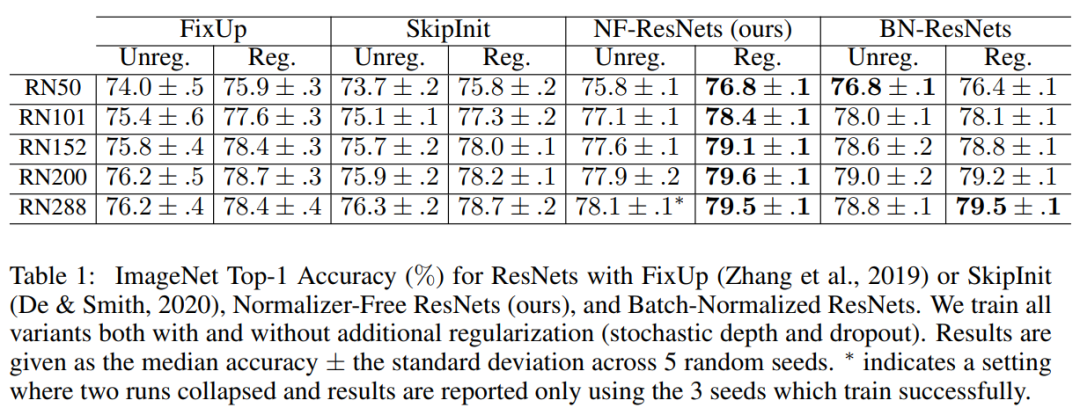
在表1中，将网络(NF-ResNets)的性能与BaseLine(BNResNets)进行了比较，这些网络的深度范围很广。在引入额外的正则化之后，NFResNets的性能优于FixUp/SkipInit，并在所有网络深度上与BN相当，正则化NF-ResNet-288实现了79.5%的最高精度。

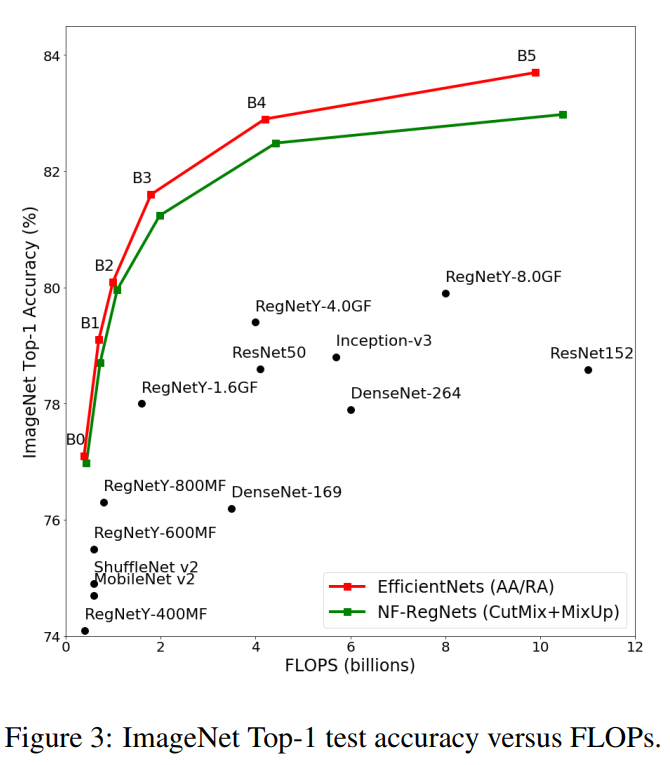
在图中比较了EfficientNets和NF-RegNets在ImageNet上的测试精度，这里对于每个数据增强NF-RegNets获得了与EfficientNets相当但略低的测试精度，同时训练速度大大提高。在数据增强中，对比自动增强(AA)或随机增强(RA)的结果发现使用CutMix+MixUp训练EfficientNets的效果更好。

然而，AA和RA都会降低NF-RegNets的性能和稳定性，因此使用CutMix+Mixup替代的NF-RegNets中的数据增强的结果。假设这是因为AA和RA是通过对批归一化模型应用架构搜索而开发的，因此当删除归一化层时，它们可能会改变数据集的统计数据，从而对信号传播产生负面影响。为了支持这个说法，在NF-RegNet的第1次卷积后插入单个BatchNorm可以消除这些不稳定性，并能够使用AA或RA进行稳定训练，尽管这种方法不能获得更高的测试集精度。

下表为对比的具体数值：

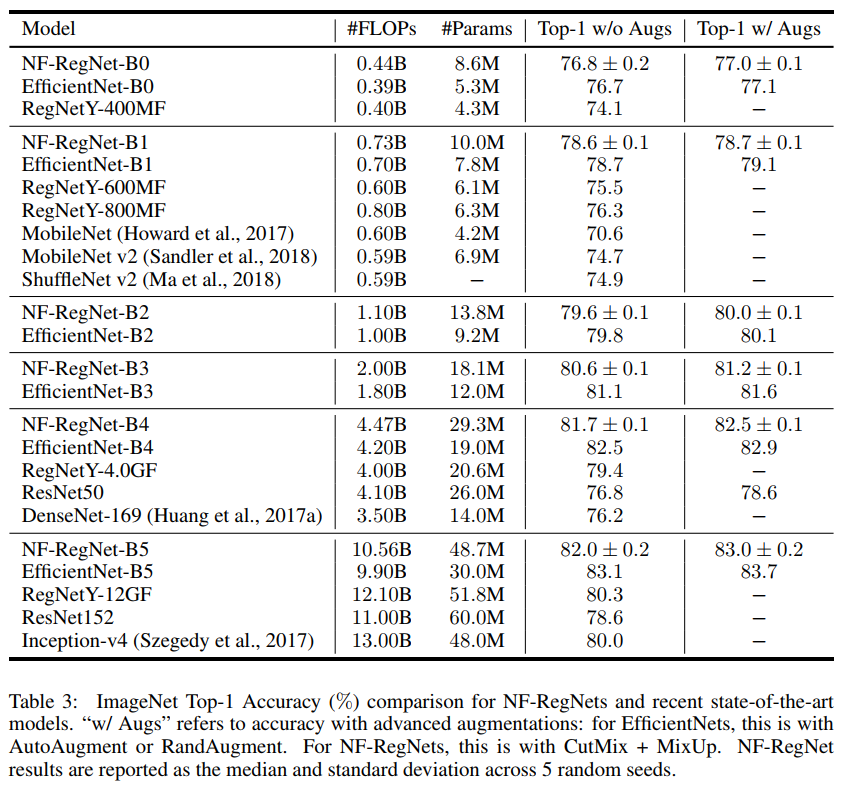
6 参考

[1].SA-NET: SHUFFLE ATTENTION FOR DEEP CONVOLUTIONAL NEURAL NETWORKS
[2].https://github.com/rwightman/pytorch-image-models/tree/master/timm/models