潘建伟团队研究再登Nature：规模化量子计算，成功求解施温格方程-技术圈

新智元报道

来源：墨子沙龙

编辑：小匀

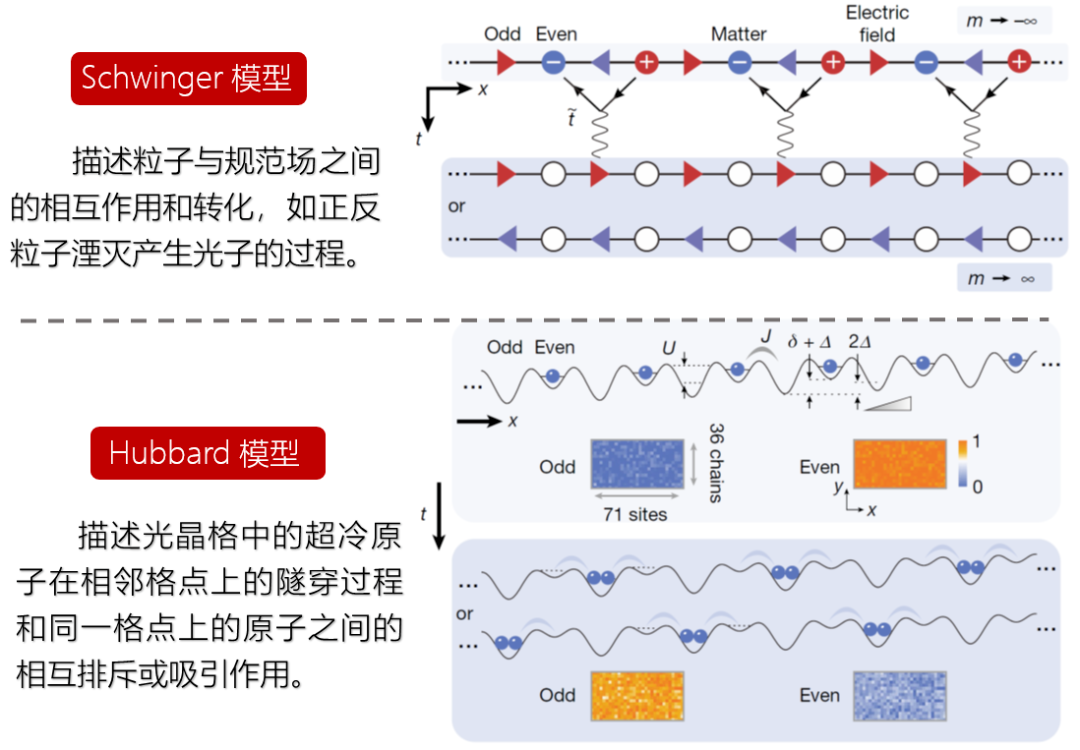
【新智元导读】中国科学技术大学潘建伟、苑震生等与德国海德堡大学、意大利特伦托（Trento）大学的合作者在超冷原子量子计算和模拟研究中取得重要突破：他们开发了一种专用的量子计算机---71个格点的超冷原子光晶格量子模拟器，对量子电动力学方程施温格模型（Schwinger Model）进行了成功模拟。今天该工作发表在《自然》杂志上。

基于规范理论，物理学家建立了标准模型，可以很好地描述组成物质世界的基本粒子及其之间的强、弱、电磁相互作用。而规范不变性作为“理论背后的理论”，是构造规范理论的基本原理。

中国科学技术大学潘建伟、苑震生等与德国海德堡大学、意大利特伦托大学的合作者在超冷原子量子计算和模拟领域取得重要突破：在71格点的光晶格量子模拟器中成功实现了对量子电动力学中方程的模拟，首次使用微观量子调控手段在量子多体系统中验证了描述电荷与电场关系的高斯定律。

此工作提供了一种新方式，利用实验上高度可控的规模化量子模拟器来探究基础物理的规范对称性。

题目为“Observation of gauge invariance in a 71-site Bose-Hubbard quantum simulator（在71格点玻色-哈伯德量子模拟器中观测到规范不变性）”的论文于北京时间11月19日发表于《自然》（Nature）杂志。

至此，潘建伟教授领导的研究团队在使用超冷原子产生大规模量子纠缠态进行量子计算、构建拓扑量子计算系统、模拟凝聚态超流模型、模拟人工规范场、开展超冷化学研究等方面取得了丰硕的原创科研成果，已在Nature(1)、Science(3)、Nature Physics(5)和PRL(8)上发表论文17篇，成为国际上超冷原子量子计算和量子模拟领域的领跑团队之一。

物理学家的终极理想——全能建筑工

如果说物理学是一座宏伟的大厦，物理学家的工作就是要弄明白，这座大厦是由哪些材料组成，这些材料是如何相互支撑构成建筑体，以及这些材料本身又是如何得到的。

对于搞建筑的人来说，你得知道，钢筋和砖块是如何相互配合达到稳固，玻璃、铝材如何搭配才能隔音，砖块之间靠什么固定，瓷砖之间如何拼接美化，如果你想在某个方向上更细致的研究，你还可以探索，砖块是怎么烧制的，什么样的涂层更加防水。

当然，如果你对涂防水层很在行，那你是一名很好的瓦工，如果你搭建木料很精通，那你是很棒的木匠，但是如果一个人既会瓦工的活，又懂木工的活，是不是就更厉害了？

物理学家的工作也十分类似。他们也想找到一种能构建物理学大厦的万能方法。

我们把时间拨回到四五百年前，开普勒所在的年代，那个时候，人类还处在懵懂中，还不知道苹果为什么会下落，太阳为什么会升起。天文学家开普勒和他的老师，利用长年累月观测到的天体运行数据，总结出了开普勒三定律。

虽然今天看来，这三大定律更像是唯象的描述，远没有触及力学的本质，但人类毕竟第一次开始根据头顶星体的运行流转，“揣测”上帝的意图。

经过伽利略等天文学家的努力，到了牛顿这儿，他建立了完整的力学和运动学体系。像我们中学熟悉的F=ma，就是这个力学体系中最广为人知的一部分。通过牛顿这套力学体系以及他的万有引力定律，不仅能推导出开普勒三定律，还能计算苹果下落和太阳升起，人们开始明白，天上地下的各种现象有了一个更统一的规律在支配。这就相当于，一个泥瓦工，找到了一种方法，不仅能用来刷墙，还能用来刷家具。

一个物理规律该怎样就是怎样，在地球上观测到的物理规律，换到月亮参考系上应该是一样的，也就是说，我们描述物理规律的一套方程，在不同的坐标系下要满足所谓的“协变性”或“不变性”。牛顿力学符合伽利略协变性，而伽利略协变性是那么的“自然”。一切是如此美好！

然而，我们不仅有牛顿力学，后来我们又有了麦克斯韦电磁理论。麦克斯韦电磁理论的建立，也经历了一个“统一”的漫长历程，人们原本以为电和磁是相互独立的，在很多物理学家的努力下，电磁理论愈发完善，最终由麦克斯韦总结，这就是我们熟悉的麦克斯韦方程组，它让我们知道了电和磁是如何相互激发、相互影响，两者是统一的。

但人们发现麦克斯韦方程组并不满足“天经地义”的伽利略坐标变换，难道客观的物理定律要依赖于主观选择的参考系？这一点都不科学！经过深入的思考，爱因斯坦等人意识到，麦克斯韦方程组也是具有协变性的，这是一种更深刻的协变性：洛伦兹协变性。

基于这一洞察，爱因斯坦提出了狭义相对论，解决了牛顿力学和麦克斯韦电磁理论的矛盾，统一了时间和空间，人们对世界有了全新的认知。电磁理论也得以有了更对称、更凝练的表述形式。

爱因斯坦不满足于此，他要把这一协变性想法从惯性系推广到非惯性系，这便有了广义协变性原理，即客观的物理规律应该在任意坐标系（包括非惯性系）下都成立。经过十年的思考和探索，广义相对论诞生了！引力得到了“满意”的描述，困惑牛顿和爱因斯坦的超距作用消失了。

在广义相对论框架下，引力只不过是时空弯曲的表现。“时空告诉物质如何运动,物质告诉时空如何弯曲”，整个宇宙的时空是一个四维的曲面，大到天体，小到苹果，都在这个舞台上演绎着自己的故事。这一次，引力和几何统一在了一起。

爱因斯坦的想法，启发了很多物理学家和数学家。在广义相对论提出几年之后，一个叫做外尔的德国数学家，希望能把电磁理论也几何化，但他无法解决“平行移动改变长度”的缺陷。1920年代，量子力学的诞生带来了新希望。在其他人工作的基础上，外尔发现在量子力学的框架下麦克斯韦理论有一个新的对称性：规范不变性。规范理论正式走上了历史舞台。

描述带电粒子和电磁场相互作用规律的量子电动力学（QED）是第一个被广泛认可的规范场。所谓规范场，即是拉格朗日量在规范变换下保持不变的场理论；因其规范变换由U(1)群来刻画，量子电动力学也被叫作U(1)规范场，这是一种阿贝尔规范场。

当然，科学家并不仅仅满足于了解电磁相互作用，如果我们深入原子核内部，还会发现另外两种相互作用。比如，质子和中子是靠强相互作用抱团的，夸克也是靠强相互作用组成质子和中子的，而再进一步缩小尺度，夸克、中微子这些微观粒子，在距离极小的尺度上，则主要是受到弱相互作用的支配。那么，这两种相互作用是不是也可以用“规范场”来表示呢？是不是也存在某种协变性呢？

1954年，杨振宁和米尔斯在研究强相互作用问题的时候，发明了一种数学方法，他们把阿贝尔规范场U(1)推广到了非阿贝尔规范场SU(2)，这成为了规范场理论划时代的一步。SU(2)后来被用来刻画弱相互作用，其有3（2^2 -1 = 3）个生成元，对应于传递弱相互作用的3种规范波色子W+、W-、Z。

以此为基础，量子色动力学理论也建立起来，人们用SU(3)规范场刻画强相互作用，SU(3)也是一种非阿贝尔规范场，其有8（3^2 -1 = 8）个生成元，对应传递强相互作用的8种胶子。

引力相互作用，电磁相互作用，强相互作用，弱相互作用，四大工种各据一方，物理学家们开始想办法练就一种神功，能一次搞定四种技能，练成之后，瓦工、木工、电工都手到擒来，物理学大厦建成也就近在眼前。

格拉肖、温伯格、萨纳姆三位物理学家把弱相互作用和电磁相互作用统一在了GWS弱电理论下，并因此获得了1979年的诺贝尔物理学奖；后来，标准模型又把强相互作用包括进来，自此三大工种被统一到了一个框架下。

现在就剩最后一步，把引力相互作用包含进来。可是这一步到目前为止也没有得到解决。标准模型定义在平坦的4维闵可夫斯基空间上，而引力由非0曲率的赝黎曼流形来描述，两者有各种“不兼容”。尽管如此，物理学家还是在努力，希望有一天，真的可以统一这四种相互作用，找到物理学的终极答案。

当量子模拟遇上规范场

既然规范场理论在物理学大厦中扮演如此重要的地位，科学家们也就一直想通过计算机来求解动力学规范理论，但是规范场方程求解的计算复杂度非常高，即便是经典的超级计算机，也面临着巨大的困难，而量子模拟（计算）具有与经典计算不同的运行模式，在复杂问题求解上已经展现出诱人的前景。

“自然不是经典的，如果你想对自然进行模拟，那么你最好把计算机给量子化。”

早在1982年，著名物理学家理查德·费曼就提出了利用一个可控的人造量子系统来模拟另一个我们感兴趣的现实的复杂量子体系的原始想法。随着最近几十年技术的发展，人们可以对越来越大的量子体系实现每个原子、分子等的精细操控，量子模拟不断取得突破，在量子多体问题、高温超导、量子化学、原子分子物理以及基础物理等领域已经发挥了重要作用。

针对规范理论动力学的量子模拟，研究人员也已经在陷俘离子、超导量子比特、冷原子等不同物理体系中开展了一些理论和实验工作。

相较于对凝聚态物理、材料结构、化学反应的量子模拟，无论理论上还是实验上，模拟规范理论都具有更大的困难，这主要体现在：规范理论既包含描述基本粒子的费米子场，也包含传递相互作用的规范玻色子场，必须实现对这两种自由度的模拟；为了保证因果结构，必须在低能、非相对论性的多体量子体系中实现相对论性的洛伦茨不变性；同时还必须实现局域的规范不变性的模拟，这是“规范荷”守恒和相互作用性质的要求，例如在量子电动力学中，需要保证电荷守恒和高斯定律。

在超冷原子体系中模拟规范不变性

量子电动力学、量子色动力学等规范理论是时空连续的，因此对其进行非微扰处理时会遇到无限维路径积分的计算，这使得问题变得棘手。

而格点规范理论（Lattice Gauge Theories，LGT）将时空离散化，即以有限的格点上的物理量来替代连续时空中的场，格点通过链路（link）相连。

通常，费米场（物质场）被定义在格点上，而玻色场（传递相互作用）被定义在链路上。通过把四维欧几里得时空离散化，路径积分变成了有限维，方便使用蒙特卡洛等模拟方法对问题进行数值求解。格点规范理论是处理量子场论最有效的非微扰方法之一，同时与连续的规范理论相比，也更适合于用光晶格体系对其进行量子模拟。

量子链路模型（Quantum Link Models，QLMs）的表述形式很好地把握住了量子电动力学的核心特征，且特别适合光晶格体系对规范理论的模拟。采用格点链路Schwinger模型，物质场、规范场及其相互作用被变换为实验中的粒子数产生、湮灭算符。

一维格点Schwinger模型描述正反粒子通过电场传递相互作用，而正负粒子湮灭后转化成了电场激发；一维Hubbard模型描述光晶格中的冷原子隧穿和相互作用的过程。在特定的势阱形状下，一维Hubbard模型与Schwinger模型的群对称性相同。（文中图示由苑震生教授提供）

一维格点Schwinger模型描述粒子与规范场之间的相互作用和转化，体现了格点规范理论的核心特征，而Bose-Hubbard模型描述光晶格中的超冷原子在相邻格点上的隧穿过程和同一格点上的原子之间的相互排斥或吸引作用，适合用光学超晶格物理体系来模拟。

研究团队在这两种模型之间建立起映射关系，规范理论中的“电荷”和“电场”可以通过光晶格上粒子数的分居情况以及格点间的粒子数密度关联来表征。不同的物理体系，其深层的数学结构却往往具有相似性，通过对一个实验上高度可控的量子系统进行调节，使其与另一个实验上难以驾驭的复杂体系具有同构的数学结构，从而完成对后者的模拟，这正是量子模拟的精神所在。

规范场理论描述基本粒子之间的相互作用、产生和湮灭过程，这一过程可以用晶格中超冷原子之间的相互作用及其在晶格中的排布模式来模拟。

实验上，研究团队首先实现了1万个Rb87原子的二维玻色-爱因斯坦凝聚，然后利用团队最近开发的冷却技术（ Science 369, 550-553 (2020)，完成了原子完美排列的人工晶格的制备，从中择取出一块71格点×36 格点的区域用于规范理论的模拟。

71格点的链长超过之前所有类似工作所使用的量子多体体系，大尺度的量子模拟器可以规避掉边界效应的影响，而在热力学极限下，这些尺寸相关的效应是不应该存在的。

另外，中国科大研究团队之前还开发了独特的自旋依赖超晶格、显微镜吸收成像、粒子数分辨探测等量子调控和测量技术，解决了相干调控的粒子数太少和无法同时产生规范场、物质场的两个主要问题。

完成具有特定原子分布结构的初态的制备，然后缓慢调节晶格的势能，让系统绝热演化，并发生相变。通过跟踪一组格点（一组3个格点分别对应于“电荷”和“电场”）上状态的相干演化，研究人员对刻画电场、电荷关系的高斯定律进行了检测，发现对高斯定律的违背大约在~10%，处于误差范围之内。

而之前的类似工作，或者由于量子模拟器太小，尺寸效应掩盖了规范理论的核心特征，例如在Science 367, 1128–1130 (2020)等工作中，由于只有2~4个格点，对高斯定律的违背高达50%，不具备局域规范不变性；或者如Nature 551, 579 (2017)等工作，由于没能实现超晶格结构，只能对阵列上的每个原子同时编码，无法分别描述粒子场、规范场，因此无法模拟两者的协同演化，无法对局域规范不变性进行检验。

研究团队成功开发出一种可以模拟U(1)规范理论且实验上高度可控的量子模拟器，并在其上首次实现了规范不变性。而描述强相互作用的量子色动力学以及粒子物理的标准模型，其规范变换分别由规范群SU(3)和SU(3)×SU(2)×U(1)来描述，通过方法和实验技术的进一步改进，研究团队有望实现对这些更复杂的规范理论的模拟。

论文链接：

https://www.nature.com/articles/s41586-020-2910-8

（感谢苑震生教授对本文的指导与帮助）