卷起来,浅析堆排序算法!
一、算法描述
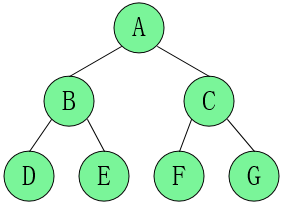
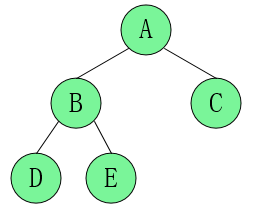
是一颗完全二叉树(Complete Binary Tree)
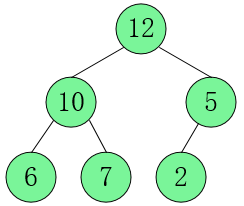
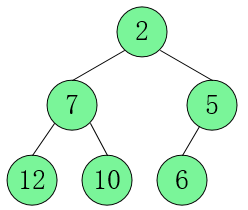
堆上面的每一个节点都必须满足父结点的值大于等于子结点的值或者父结点的值小于等于子结点的值 。parent >= children or parent <= children
二、完全二叉树
三、大顶堆和小顶堆
四、堆的性质
例如我们已经有一个大顶堆,那么这个大顶堆具有哪些特征呢?
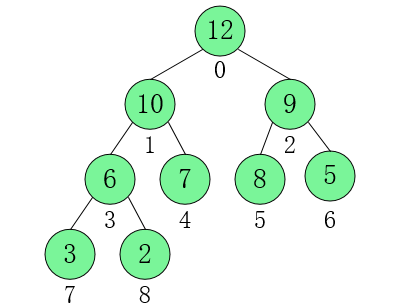
将其映射为数组:
int arr[] = {12,10,9,6,7,8,5,3,2}

我们假设结点 6 的位置为 i = 3。那么我们可以求出,他的父节点和两个子结点。
Parent = ( i - 1 ) / 2,等于位置为 1 的结点 10。
C1 = 2i + 1,等于位置为 7 的结点 3 。
C2 = 2i + 2,等于位置为 8 的结点 2 。
五、图解堆排序算法
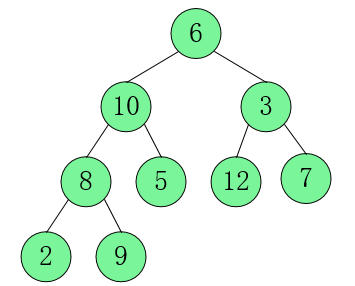
我们以 int tree[] = {6, 10, 3, 8, 5, 12, 7, 2, 9} 为例,对堆排序的执行过程进行图解。
第一步:通过原始序列构造一个大顶堆(升序采用大顶堆,降序采用小顶堆)。
1. 先通过序列通过从上到下从左往右的顺序构造一个完全二叉树。
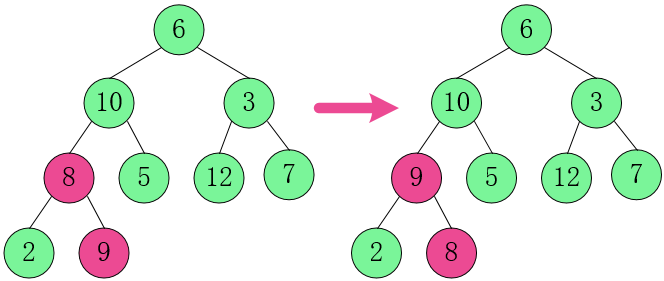
2. 对第三层的父节点和第四层的子结点进行调整,其中粉红色代表发生交换的结点。使得其父节点大于两个子结点。
即也是从最后 1 个非叶子结点开始 (8 - 1) / 2 = 3, 也就是从 8 开始进行从左到右从下到上进行调整。
[8,2,9] 中,9 最大,交换 8 和 9。
3. 对第二层父节点和第三层子结点进行调整。
[10,9,5] 中,10 最大,不交换。
[3,12,7] 中,12 最大,交换 3 和 12。

4. 对第一层父节点和第二层子结点进行调整。
[6,10,12] 中,12 最大,交换 6 和 12。
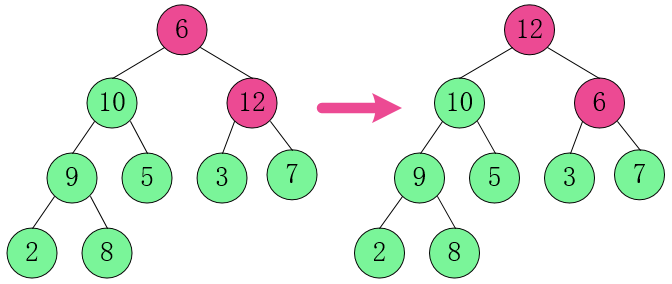
这时,上面操作导致 [6,3,7] 不是一个大顶堆,继续调整。
[6,3,7] 中,7 最大,交换 6 和 7。
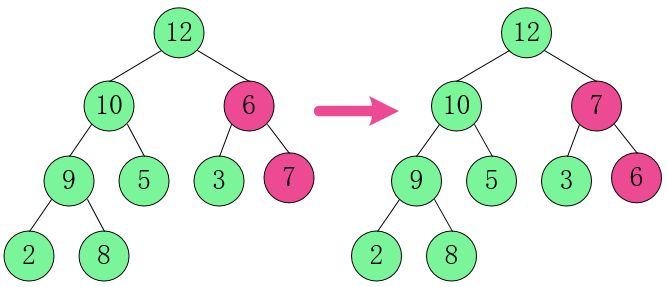
至此,大顶堆构建完成。
第二步:将根结点调整到最后一个位置,使末尾元素最大。然后对剩下元素继续调整堆,根结点调整到最后一个位置,得到第二大元素。如此反复进行交换、重够、交换。
1. 将根节点元素 12 跟 8 交换。
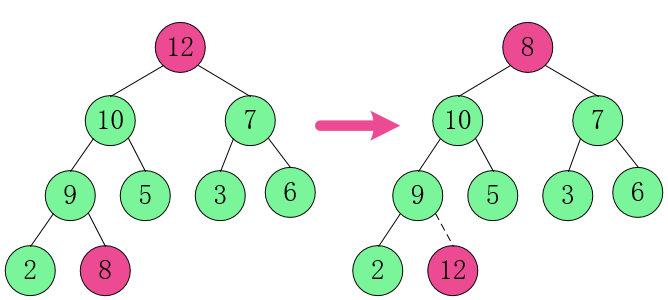
2. 重新调整结构,使其继续满足堆定义。
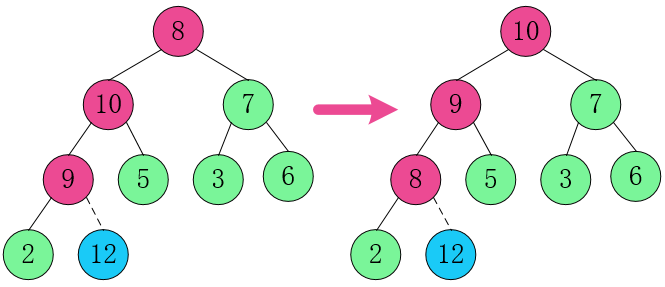
3. 将根节点元素 10 跟 2 交换。
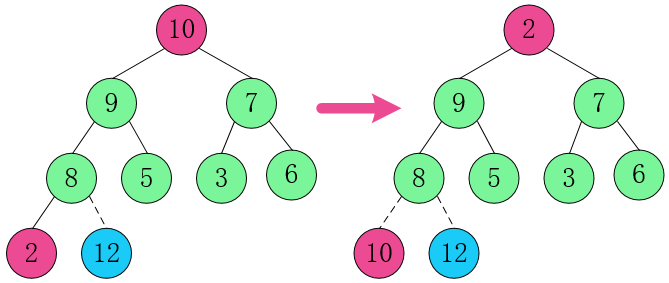
4. 重新调整结构,使其继续满足堆定义。
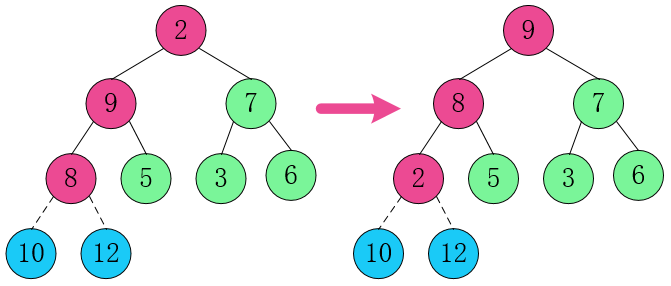
这样一直交换、重够、交换下去.......
5.最后一次将根节点元素 3 跟 2 交换。
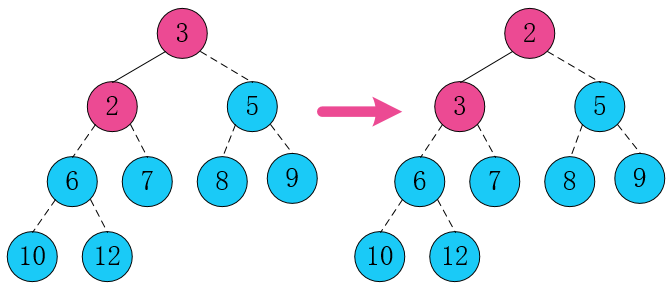
这样所有元素就达到了有序状态。
六、算法实现
第一步:构建大顶堆
#include
void swap(int arr[], int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void heapify(int tree[], int n, int i){
if (i >= n){
return;
}
int c1 = 2 * i + 1;
int c2 = 2 * i + 2;
int max = i;
if (c1 < n && tree[c1] > tree[max]){
max = c1;
}
if (c2 < n && tree[c2] > tree[max]){
max = c2;
}
if (max != i){
swap(tree, max ,i);
heapify(tree, n, max);
}
}
void build_heap(int tree[], int n){
int last_node = n - 1;
int parent = (last_node - 1) / 2;
for (int i = parent; i >= 0; i--){
heapify(tree, n, i);
}
}
void heap_sort(int tree[], int n){
build_heap(tree, n);
for (int i = n - 1; i >= 0; i--){
swap(tree, i, 0);
heapify(tree, i, 0);
}
}
int main(){
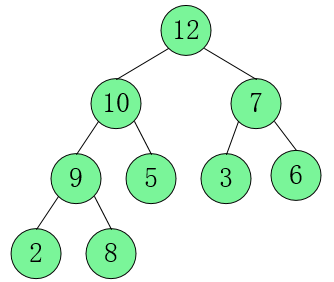
int tree[] = {6, 10, 3, 9, 5, 12, 7, 2, 8};
int n = 9;
build_heap(tree, 9);
// heap_sort(tree, 9);
for(int i = 0; i < n; i++){
printf("%d\n",tree[i]);
}
return 0;
}
输出:
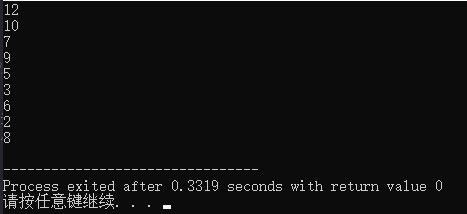
我们将它画出来康康:
第二步:排序
#include
void swap(int arr[], int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void heapify(int tree[], int n, int i){
if (i >= n){
return;
}
int c1 = 2 * i + 1;
int c2 = 2 * i + 2;
int max = i;
if (c1 < n && tree[c1] > tree[max]){
max = c1;
}
if (c2 < n && tree[c2] > tree[max]){
max = c2;
}
if (max != i){
swap(tree, max ,i);
heapify(tree, n, max);
}
}
void build_heap(int tree[], int n){
int last_node = n - 1;
int parent = (last_node - 1) / 2;
for (int i = parent; i >= 0; i--){
heapify(tree, n, i);
}
}
void heap_sort(int tree[], int n){
build_heap(tree, n);
for (int i = n - 1; i >= 0; i--){
swap(tree, i, 0);
heapify(tree, i, 0);
}
}
int main(){
int tree[] = {6, 10, 3, 9, 5, 12, 7, 2, 8};
int n = 9;
// build_heap(tree, 9);
heap_sort(tree, 9);
for(int i = 0; i < n; i++){
printf("%d\n",tree[i]);
}
return 0;
}
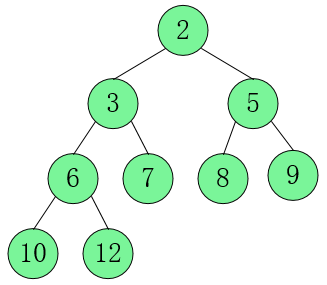
输出:
我们将它画出来康康:
就这样我们就完成堆排序啦!开不开森。
六、算法分析
时间复杂度:堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)。
空间复杂度: 因为堆排序是就地排序,空间复杂度为常数:O(1)
稳定性:不稳定。因为在堆的调整过程中,元素进行比较和交换所走的是该结点到叶子结点的一条路径,因此对于相同的元素就可能出现排在后面的元素被交换到前面来的情况。
七、适用场景
堆排序在建立堆和调整堆的过程中会产生比较大的开销,在元素少的时候并不适用。但是,在元素比较多的情况下,还是不错的一个选择。尤其是在解决诸如“前n大的数”一类问题时,几乎是首选算法。

