JS算法:图文并茂讲解堆排序
(给前端大学加星标,提升前端技能.)
作者:竹雨
https://juejin.cn/post/6932718585173753869
前言
文中用 JavaScript 实现算法,详细解释堆排序 js 中堆的创建与维护,以及堆排序算法的实现堆创建。
理论
堆,是具有下列性质的完全二叉树:每个节点的值都小于等于其左右孩子节点值是小根堆;(大于等于则是大根堆)。批注:有些参考书将堆直接定义为序列,但是,从逻辑结构上讲,还是将堆定义为完全二叉树更好。虽然堆的典型实现方法是数组,但从逻辑的角度上讲,堆实际上是一种树结构。
对于数组实现的堆,是一个完全二叉树,其中任意一个节点 i 都满足以下公式
Parent(i) = floor((i-1)/2),i 的父节点下标 Left(i) = 2i + 1,i 的左子节点下标 Right(i) = 2(i + 1),i 的右子节点下标
思路
此思路用于将任意数组调整成大根堆 首先将数组想象成是一个完美二叉树 我们的目的是将这个二叉数调整成大根堆,即每个节点的值都大于等于其左右孩子节点值 首先,寻找到最后一个根节点,此根节点有一个孩子是数组的最后一个元素 然后找出大的孩子节点与根节点对比,如果大的孩子节点比根节点大,则将根节点与大的孩子节点互换,保证根节点最大 接着向前遍历根节点 对每个根节点,都首先找出比较大的孩子节点,然后将大的孩子节点与根节点对比 如果孩子节点比根节点大,那么将孩子节点与根节点互换 然后将互换后得到新值的孩子节点作为新的根节点,将其与它自己的子节点再重复以上对比,以此进行深度遍历的重复操作,直到此相关树上的根节点都比孩子节点大为止 深度遍历操作完后,继续执行前面的根节点遍历操作,直到遍历到最后一个根节点
例子
现有数组 arr = [5,8,3,5,2,99,22,44],将其调整为大根堆 数组可以表示堆即完美二叉树,因此将其转化成完美二叉树理解(此处可自行搜索,完美二叉树用数组表示),如下图所示
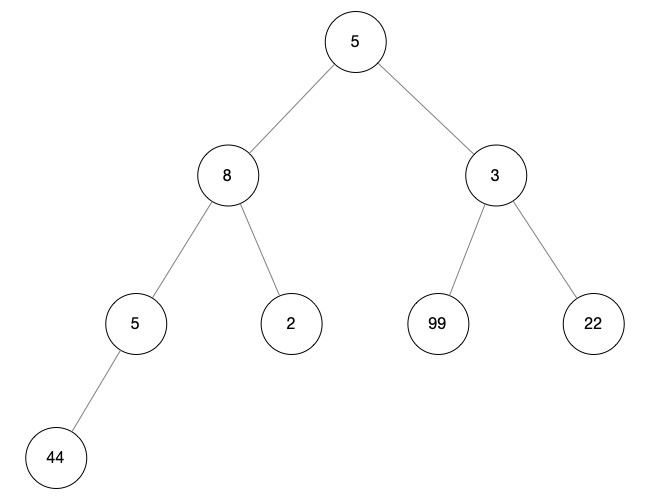
寻找最后一个根节点,用 i 表示,从 arr.length / 2 作为初始值向前查找 当 i = arr.length / 2 = 4 时没有孩子节点,所以它不是根节点 向前遍历节点,当 i = 3 时,它拥有孩子节点 arr[arr.length - 1],所以 arr[3] = 5 就是我们想找的最后一个根节点 此时我们可以得最后一颗子树,如下图标记所示
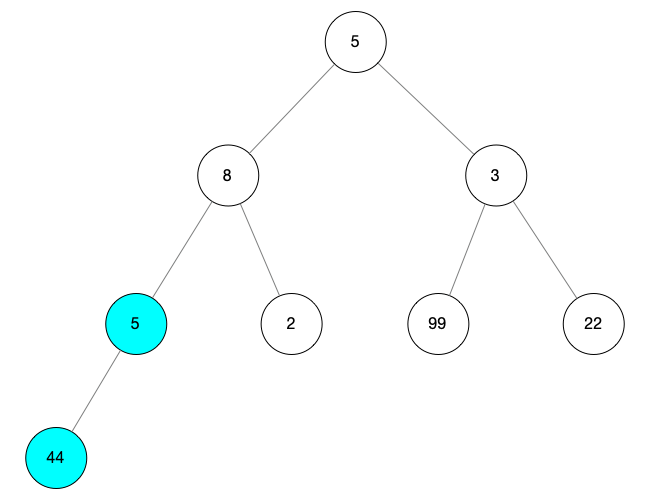
然后我们针对这颗子树进行调整操作
找到最大的孩子节点,用 child 表示,此时只有一个孩子节点 arr.length - 1,所以 child = arr.length - 1 = 7 将 child 与根节点(i = 3)对比,如果 child 的值 i 的值大,则互换值 此处 child 比 i 的值大所以互换值,child 的值改为 5,i 的值改为 44 由于 child 没有孩子节点所以不进行更深层次的遍历 操作完之后如下图所示
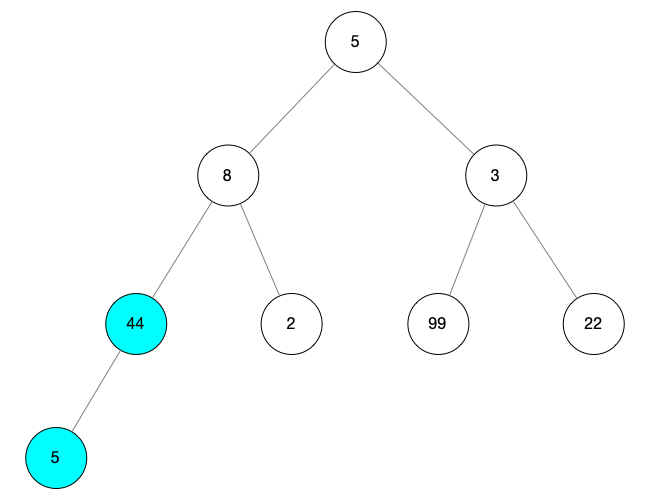
然后向前继续寻找根节点,当 i = 2 的时候,我们将找到一颗新的子树
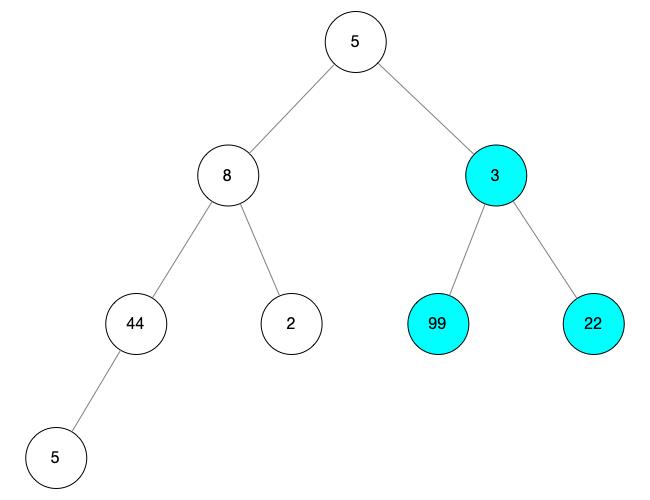
对这颗找到的树进行调整操作
寻找大的孩子节点,用 child 表示,由图可知最大的孩子节点的值为 99,所以 child = 5 当前的根节点 i = 2,由于 child 的值比 i 的值大,所以互换 同时由于 child 后面没有孩子节点,所以结束操作 上面操作后可得到下图所示的树
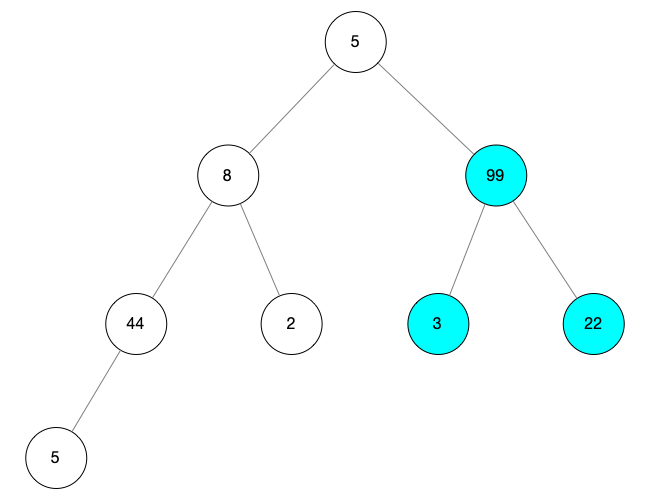
继续向前寻找根节点,当 i = 1 的时候,我们找到一颗新的树
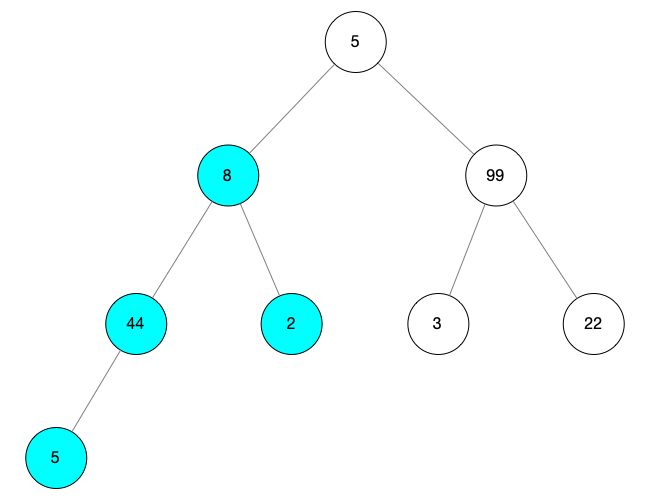
对这颗树进行调整操作,此时 i = 1,child = 3
按照上面步骤,首先互换 child 和 i 的值
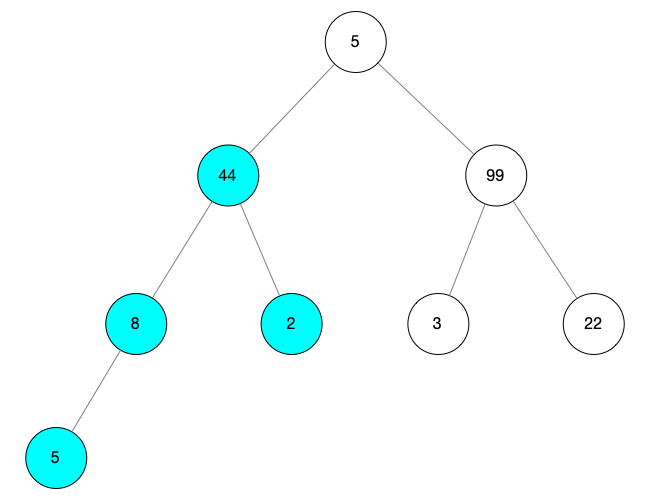
然后由于 child 有孩子节点,所以将 i 指向 i,将 child 指向它自己的孩子节点 得到 i = 3, child = 7 重复比较操作,如果孩子节点比根节点大互换值 此处 arr[i] = 8,arr[child] = 5 根节点比孩子节点大,所以不替换 最终得到的树如下图所示

继续向前遍历,得到最后一颗新树,根节点为 i = 0
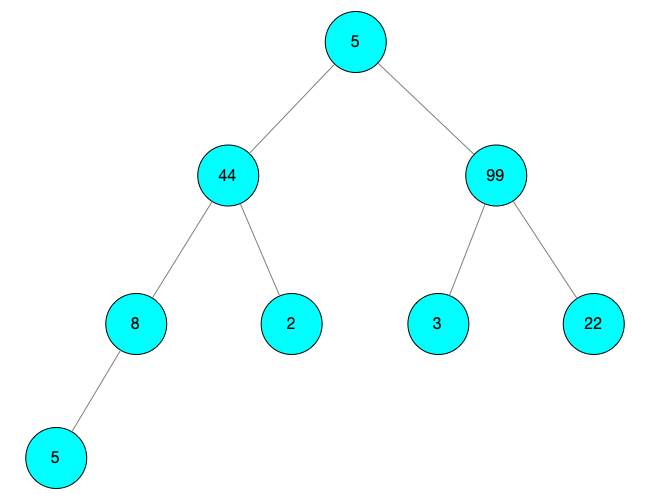
对这颗树进行调整操作
此时 i = 0 先寻找 child = 2,arr[child] = 99 arr[child] = 99 > arr[i] = 5,互换得到 arr[child] = 5,arr[i] = 99
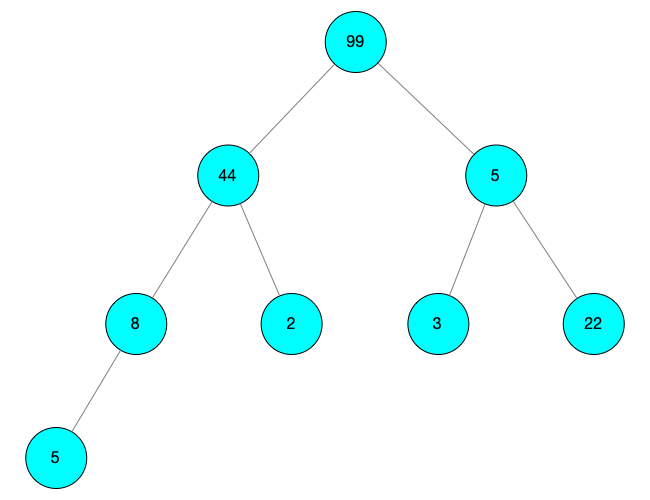
由于 child 有孩子节点,所以对 child 的孩子节点进行深度调整 i = child = 2,child = 2 * i + 1 = 5 由于此时有左右两个孩子节点,索引分别为 5 和 6,并且索引为 6 的节点值比较大,所以 child 更改为 6 比较 i 与 child 的值 arr[i] = arr[2] = 5 小于 arr[child] = arr[6] = 22 所以进行值互换,得到 arr[i] = 22,arr[child] = 5
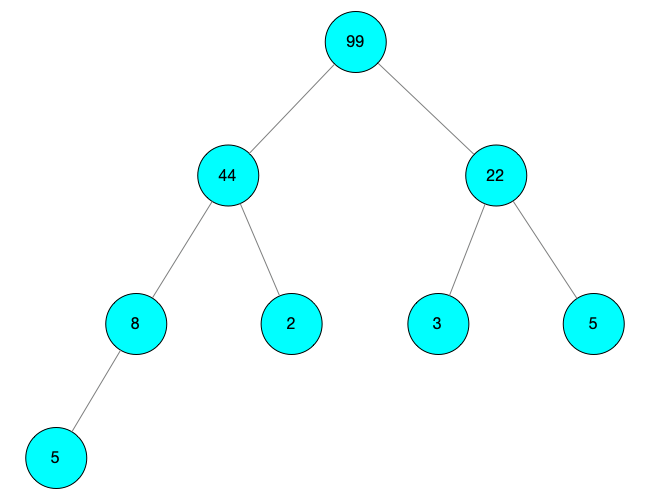
此时 child 没有孩子节点,停止深度调整 最终得到大根堆如下图所示

用数组进行表示则为:[99, 44, 22, 8, 2, 3, 5, 5]
代码
/**
* 此代码建议 mock 数据,并将其绘制成完美二叉树,参照二叉树进行阅读
*/
function buildHeap(data){
let len = data.length
// 从最后一个根节点开始,向前遍历所有根节点
// 取 len / 2 作为 i 的初始值,是因为最后一个孩子节点是 len - 1
// 它可能是左孩子也可能是右孩子,那么可以根据公式算出对应的根节点
// 它一定在 len / 2 附近,且小于 len / 2
for(let i = Math.floor(len / 2); i >= 0; i --){
heapAjust(data, i, len);
}
}
/**
* 调整操作
* 根据传入的数据调整二叉树
* i 为根节点的 key
* len 为需调整数据的长度
*/
function heapAjust(data, i, len){
// 寻找 i 的左孩子
let child = 2 * i + 1
// 如果 child 大于 len 说明 i 不是根节点
while(child < len) {
// 比较两个孩子节点,将 child 指向大的那个
if(child + 1 <= len && data[child] < data[child + 1]){
child = child + 1
}
// 如果孩子节点比根节点大,两个节点互换
if(data[i] < data[child]){
let temp = data[i]
data[i] = data[child]
data[child] = temp
// 互换之后将被更新的孩子节点继续作为根节点,进行深度查找
i = child
child = 2 * i + 1
}
else {
break
}
}
}
堆排序
思路
先将整个数组调整成大根堆 则数组的第一个元素最大,将其与数组最后一个元素替换,此时大根堆被破坏 重新调整前 length - 1 个元素,将它们调整成新的大根堆 以此循环,直到堆中的元素只有一个时
代码
var arraySort = function(arr) {
// 将数组调整成大根堆
buildHeap(arr);
// 下面需要注意的时候参数的边界
for(let i = arr.length - 1; i >= 0; i --) {
// 互换数据
let temp = arr[i]
arr[i] = arr[0]
arr[0] = temp
// 将前面的元素重新调整成大根堆
heapAjust(arr, 0, i-1);
}
}
总结
堆排序是不稳定的 在寻找前几个值最大的场景中比较好用
点赞和在看就是最大的支持❤️
评论
