【论文导读】浅谈胶囊网络与动态路由算法
前言
“Dynamic Routing Between Capsules”是由Hinton等联合发表在NIPS会议上。提出了一个新的神经网络---胶囊网络与囊间的动态路由算法。
上篇文章中提到了动态路由算法,由于没太理解,因此找了原论文并且结合参考文献的4篇博文进行解读,才对胶囊网络与动态路由算法的过程有了一点认识。本篇文章的所有图片来源都是来自4篇博文,并且参考了其中部分知识。对胶囊网络有兴趣的同学可以阅读下,非常有帮助。
本篇文章约3.2k字,预计阅读12分钟。
1. 作者
本篇论文是由Sara Sabour、Nicholas Frosst与Geoffrey E. Hinton联合发表。对于胶囊网络(Capsules Net)的提出者之一Geoffrey E. Hinton(「杰弗里·埃弗里斯特·辛顿」),我们应该了解下:
❝他是「反向传播算法」、「对比散度算法」和「波尔兹曼机」的发明人之一,也是深度学习的积极推动者,被誉为“「深度学习之父」”。因在深度学习方面的贡献与约书亚·本希奥和杨立昆一同被授予了2018年的图灵奖。----- 维基百科
❞
2. 背景
2.1 CNN的特性与缺陷
卷积神经网络(CNN)在图像分类上取得了非常显著的效果。它有几个非常重要的特性:
「平移不变性(translation invariance )」:简单来说不管图片的内容如何进行平移,CNN还能输出与之前一样的结果。为什么具有平移不变性?这个性质由全局共享权值和Pooling共同得到的; 「平移等变性(translation equivariance)」:对于一个函数,如果你对其输入施加的变换也会同样反应在输出上,那么这个函数就对该变换具有等变性。这由局部连接和权值共享决定;
例:
❝如果输出是给出图片中猫的位置,那么将图片中的猫从左边移到右边,这种平移也会反应在输出上,我们输出的位置也是从左边到右边,那么我们则可以说CNN有等变性;如果我们只是输出图片中是否有猫,那么我们无论把猫怎么移动,我们的输出都保持”有猫”的判定,因此体现了CNN的不变性。---引自http://www.lunarnai.cn/2018/03/23/CNN_euivariant_invariant/
❞
「不具备特性」:
「旋转不变性」:做过简单的图像分类就应该知道,当我们为了增强模型性能,总是会做图像增强的工作,其中就包括旋转,这就是为了克服CNN不具备旋转不变性的缺陷;
根据以上信息我们可以得出「结论」:CNN擅长检测特征,但在探索特征之间的「空间关系」(大小,方向)「方面效果不佳」。例如,对于以下扭曲的人脸图,CNN可能会认为这是一张正常的人脸。

2.2 最大池化(Max Pooling)的缺陷
作者认为Max Pooling在每一层仅保留最活跃的特征,而忽略了其他的特征,即损失了有价值的东西。
❝This type of “routing-by-agreement” should be far more effective than the very primitive form of routing implemented by max-pooling, which allows neurons in one layer to ignore all but the most active feature detector in a local pool in the layer below.
❞
3. 胶囊网络
简单的CNN模型可以正确提取鼻子,眼睛和嘴巴的特征,但会错误地激活神经元以进行面部检测。如果没有意识到「空间方向和大小」上的不匹配,则面部检测的激活将太高【简单来说,并不是存在眼睛、鼻子、嘴巴就一定是一张脸,还有考虑各个部位的方向问题、大小问题等】。
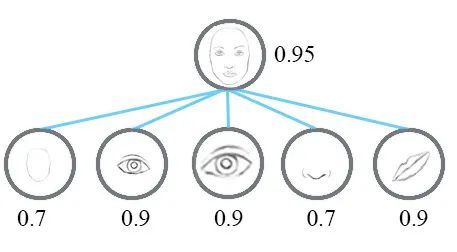
但是,如果每个神经元都包含特征的概率和其他属性。例如,它输出一个包含[可能性,方向,大小]的「向量」。有了这些空间信息,就可以检测到鼻子,眼睛和耳朵的特征在方向和大小上的不一致,从而为面部检测输出低得多的激活力。
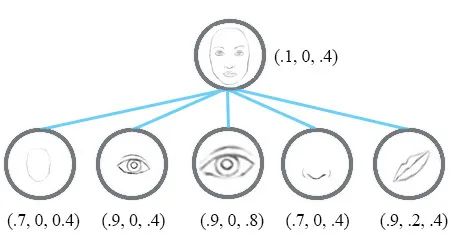
「因此用向量来代替单个神经元标量」,即文章提到的“胶囊”(Capsule),形成了胶囊网络。
3.1 胶囊
以下通过原文的描述对胶囊下一些定义:
1、一个胶囊是一组神经元(「输入」),即神经元「向量」(activity vector),表示特定类型的实体(例如对象或对象部分)的实例化参数(例如可能性、方向等)。
❝A capsule is a group of neurons whose activity vector represents the instantiation parameters of a specific type of entity such as an object or an object part.
❞
2、「使用胶囊的长度(模)来表示实体(例如上述的眼睛、鼻子等)存在的概率」,并使用其方向(orientation)来表示除了长度以外的其他实例化参数,例如位置、角度、大小等。
❝We use the length of the activity vector to represent the probability that the entity exists and its orientation to represent the instantiation parameters.
❞
❝In this paper we explore an interesting alternative which is to use the overall length of the vector of instantiation parameters to represent the existence of the entity and to force the orientation of the vector to represent the properties of the entity.
❞
3、胶囊的「向量输出」的长度(模长)不能超过1,可以通过应用一个「非线性函数」使其在方向不变的基础上,缩小其大小。
❝cannot exceed 1 by applying a non-linearity that leaves the orientation of the vector unchanged but scales down its magnitude.
❞
接下来我们主要介绍胶囊之间的传播与训练过程。
3.1.1 问题定义
胶囊网络总的计算过程如下所示(图来自[4]):
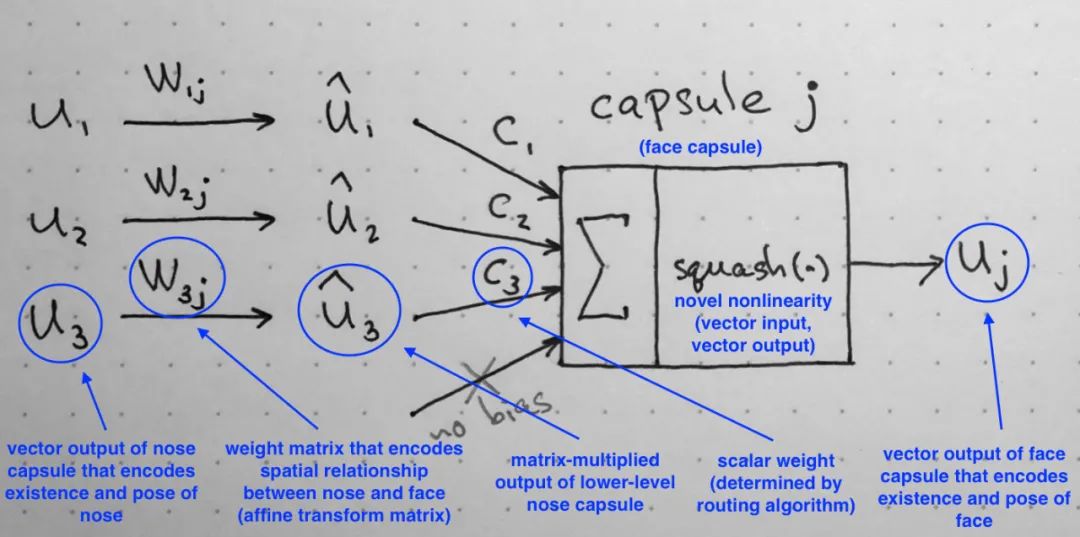
我们假设低层次的胶囊(输入)是探测眼睛、嘴巴、鼻子,整个胶囊网络的目的(输出)是探测人脸。为了与普通神经网络相比,完全可以将胶囊网络的计算看成前向传播的过程。
3.1.2 低层胶囊输入
输入为较为低层次的胶囊(Primary Capsule),其中,表示胶囊的个数,表示每个胶囊内的神经元个数(向量长度)。图中的可以解释为监测到眼睛、嘴巴、鼻子三个低层次的胶囊。
3.1.3 计算预测向量(predict vector)
应用一个转换矩阵(transformation matrix),表示输出胶囊的神经元数量,将输入转换为「预测向量」:
「为什么称为预测向量?」 因为转换矩阵是编码低层特征(眼睛、嘴和鼻子)和高层特征(脸)之间重要的空间和其他关系。
例如对于鼻子来说,脸以鼻子为中心,它的大小是鼻子的10倍,它在空间中的方向与鼻子的方向相对应,因为它们都在同一个平面上,因此得到的向量是对人脸的预测;其他两个向量同理,如下图所示:

对于权重矩阵,「它依旧是通过反向传播进行学习」。
3.1.4 预测向量加权求和
然后我们需要将所有得到的预测向量进行加权求和:
其中被称为高层胶囊总的输入,为权重系数,在论文中被称为耦合系数(coupling coefficients),并且。从概念上说,表示胶囊激活胶囊的概率分布,「它是通过动态路由算法进行学习」。
3.1.5 胶囊输出
之前我们提到想要一个胶囊的向量的模来表示由胶囊所代表的实体存在的概率。因此作者在论文中提出使用非线性函数“「squashing」”来替代传统的神经网络的激活函数Relu,这是为了确保短向量可以被压缩至接近0的长度,长向量压缩至接近1的长度,「并且保持向量的方向不变」。因此最终胶囊的向量输出:
对上述式子进行分析:
当为长向量时,那么; 当为短向量时,那么;
当为向量时,很难将squashing函数进行可视化,为了方便,以下为标量:
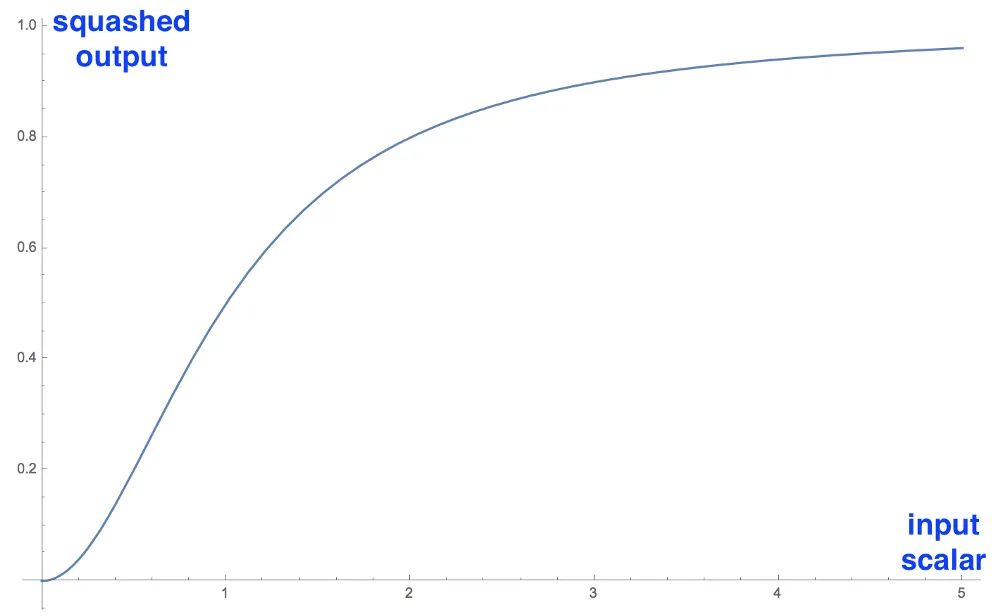
3.1.6 与普通神经网络进行比较

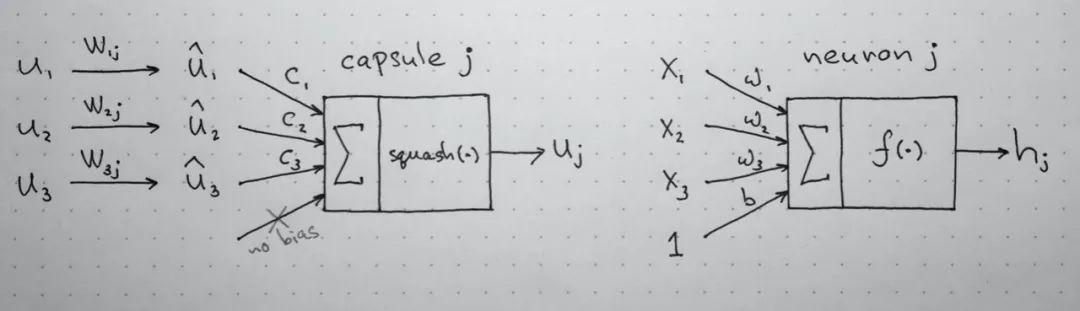
上述胶囊网络与传统的神经网络比较图片来自[4],了解神经网络结构的同学也可以对胶囊网络有更深入的认识,具体的介绍可以看[4]。
两者的计算过程如下所示:
3.2 Dynamic Routing算法
对于上述的学习参数是通过迭代的动态路由算法进行更新,以下是原文对动态路由算法的描述:

首先得到所有的「预测向量」,定义「迭代次数」,以及当前输入胶囊属于网络的第层;
对于所有的输入胶囊和输出胶囊,定义一个参数,被初始化为0,对于该参数的作用,在下一步进行描述;
开始迭代4~7步,迭代次数为;
计算向量的值,即胶囊的所有路由权值,此处为什么使用softmax?前面提到过,要保证,因此使用softmax函数来保证每个非负且和为1。
【注】:由于第一次迭代初始化为0,因此在第一轮迭代中都相等,即,是指较高层胶囊的数量;
,预测向量进行加权求和;
最后一步的向量通过非线性函数squash,这确保了向量的方向保持不变,但它的长度被强制不超过1。这一步输出最终的向量
这一步是权重发生更新的地方,也是整个动态路由算法的「关键」。这一步通过胶囊的输出与预测向量的点积+原有的权重,为新的权重值。「进行点积处理,是为了检测胶囊输入与输出的相似性」。更新权重后,进行下一轮迭代;
经过次迭代后,返回最终的输出向量;
经过上述动态路由算法的解析,我们发现动态路由不能完全替代反向传播。转换矩阵仍然使用代价函数进行反向传播训练。但是,使用动态路由来计算「胶囊的输出」。「通过计算来量化一个低层次胶囊与其父胶囊之间的联系」。
4. 总结
通过论文与参考文献中的博客的叙述,对上篇文章中使用的动态路由算法有了更清晰的认识。
参考文献
[1] https://jhui.github.io/2017/11/03/Dynamic-Routing-Between-Capsules/
[2] https://medium.com/ai³-theory-practice-business/understanding-hintons-capsule-networks-part-i-intuition-b4b559d1159b
[3] https://medium.com/ai%C2%B3-theory-practice-business/understanding-hintons-capsule-networks-part-ii-how-capsules-work-153b6ade9f66
[4] https://medium.com/ai%C2%B3-theory-practice-business/understanding-hintons-capsule-networks-part-iii-dynamic-routing-between-capsules-349f6d30418
往期精彩回顾
获取一折本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/662nyZF
本站qq群1003271085。
加入微信群请扫码进群(如果是博士或者准备读博士请说明):
